Project Euler 110:Diophantine reciprocals II 丢番图倒数II

Diophantine reciprocals II

In the following equation x, y, and n are positive integers.

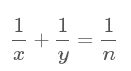
For n = 4 there are exactly three distinct solutions:

 

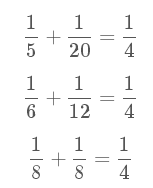
It can be verified that when n = 1260 there are 113 distinct solutions and this is the least value of n for which the total number of distinct solutions exceeds one hundred.

What is the least value of n for which the number of distinct solutions exceeds four million?

NOTE: This problem is a much more difficult version of Problem 108 and as it is well beyond the limitations of a brute force approach it requires a clever implementation.

---

丢番图倒数II

在如下方程中，x、y、n均为正整数。

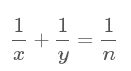
对于n = 4，上述方程恰好有3个不同的解：

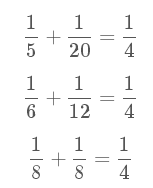
可以验证当n = 1260时，恰好有113种不同的解，这也是不同的解的总数超过一百种的最小n值。

不同的解的总数超过四百万种的最小n值是多少？

注意：这是第108题一个极其困难的版本，而且远远超过暴力解法的能力范围，因此需要更加聪明的手段。

 解题

先占坑

 待完善