机器人学——2.3-姿态插值和笛卡尔运动

之前我们提到mstraj函数并不是不是对坐标系旋转进行插值的理想方式。

在机器人学中，我们经常需要对姿态进行插值。例如，我们需要机器人的末端执行器平滑地从姿态 $xi_0$ 和改变到 $xi_1$。假设某个函数 $xi(s)=sigma(xi_0, xi_1, s)$，其中 $sin[0,1]$，可以看做是一条归一化了的路径，函数的边界条件为 $sigma(xi_0, xi_1, 0)=xi_0$，$sigma(xi_0, xi_1, 1)=xi_1$，而且 $sigma(xi_0, xi_1, s)$ 要能平滑地经过 $s$ 内定义的一系列中间位姿。我们之间已经了解了多种位姿的描述方式，我们不妨分别讨论。

如果位姿由正交旋转矩阵表示，$xisim Rin SO(3)$，如果用简单的线性插值 $sigma(R_0,R_1,s)=(1-s)R_0+sR_1$。但这是不可行的，这样插值后得到的通常不再是有效的正交矩阵，因为正交矩阵必须满足的列向量范数为1以及列向量之间正交的条件。

一般是选择三角度表示法，如欧拉角或横滚-俯仰-偏航角，$xisimGammainmathbb{S}^3$，这样就可以使用线性插值法：
$sigma(Gamma_0, Gamma_1, s)=(1-s)Gamma_0+sGamma_1$例如，我们定义了两个姿态：

>> R0 = rotz(-1) * roty(-1);
>> R1 = rotz(1) * roty(1);

得到等价横滚-俯仰-偏航角：

>> rpy0 = tr2rpy(R0);
>> rpy1 = tr2rpy(R1);

然后分50个时间步在它们之间生成一条轨迹：

>> rpy = mtraj(@tpoly, rpy0, rpy1, 50);

通过动画演示，很容易观察轨迹变化过程（rpy是一个 $50×3$ 矩阵，而rpy2tr的结果是 $4×4×50$ 矩阵。）：

>> tranimate(rpy2tr(rpy));

由于姿态变化较大，可以看出坐标系的旋转轴线沿轨迹的变化。这个动作虽然平滑，但有时看起来也不太协调。另外，如果在所采用的三角度系统中有 $xi_0$ 或 $xi_1$ 与之一接近奇异点，也会出现问题。

采用单位四元数的插值法只比三角度向量法复杂一点点，它在空间中产生一个绕固定轴旋转的姿态变化。首先，我们利用机器人工具箱函数找到与这两个位姿等价的四元数：

>> q0 = Quaternion(R0);
>> q1 = Quaternion(R1);

然后对它们进行插值并进行动画演示：

>> q = interp(q0, q1, [0:49]'/49);
>> about(q)
q [Quaternion] : 1x50 (1.6 kB)
>> tranimate(q)

四元数插值法是通过使用球形线性插值（slerp）来实现的，其中单位四元数要在一个四维超球面上沿一个大圆路径运动。而在三维空间中的结果就是绕定轴的转动。

笛卡尔运动

另一个常见的需求是在 $SE(3)$ 中生成两位姿之间的光滑路径，它同时涉及位置及姿态的变化。在机器人学中这通常被称作笛卡儿运动。我们将初始和最终位姿都表示成齐次变换矩阵：

>> T0 = transl(0.4, 0.2, 0) * trotx(pi);
>> T1 = transl(-0.4, -0.2, 0.3) * troty(pi/2) * trotz(-pi/2);

工具箱函数trinterp提供了沿路径单位化距离 $sin[0,1]$ 中的位姿插值。例如，其中间的位姿是

>> trinterp(T0, T1, 0.5)
ans =
    0.6667   -0.3333    0.6667         0
   -0.6667   -0.6667    0.3333         0
    0.3333   -0.6667   -0.6667    0.1500
         0         0         0    1.0000

其中平移部分是用线性插值，旋转部分是用四元数插值法interp进行球形插值。
两个位姿之间 $50$ 个分步的轨迹可用以下方法生成：

>> Ts = trinterp(T0, T1, [0:49]'/49);

参数分别对应的是起点和终点的位姿，以及从 $0$ 到 $1$ 线性变化的路径长度。由此产生的轨迹Ts是一个三维矩阵：

>> about(Ts)
Ts [double] : 4x4x50 (6.4 kB)

代表的是每个时间分步（第三个指数 $50$ ）对应的齐次变换矩阵（前两个指数 $4×4$ ）。其中，路径上第一点的齐次变换是：

>> Ts(:,:,1)
ans =
    1.0000         0         0    0.4000
         0   -1.0000         0    0.2000
         0         0   -1.0000         0
         0         0         0    1.0000

最简单直观的表现方法仍然是通过动画：

>> tranimate(Ts)

它将展现出坐标系从位姿T1平移、旋转到位姿T2的变化过程。
该轨迹的平移部分由以下方式获得：

>> P = transl(Ts);

它将以矩阵形式返回轨迹的笛卡儿位置坐标：

>> about(P)
P [double] : 50x3 (1.2 kB)

可以看出，P有 $50$ 行 $3$ 列，每一行对应每个时间分步上的位置向量。
位置向量的变化可以用plot 函数画出：

>> plot(P)

以横滚-俯仰-偏摆角格式画的姿态变化曲线：

>> rpy = tr2rpy(Ts);
>> plot(rpy);

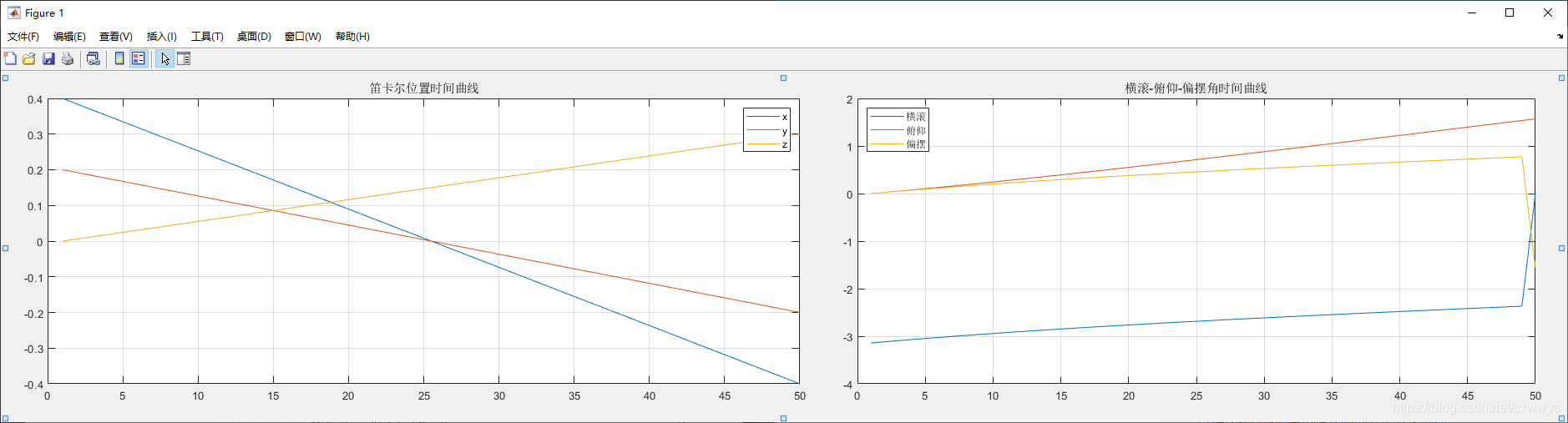
从图中看到，位置坐标随时间的变化既平滑又呈线性，而姿态随时间的变化也平滑，但不是线性的。横滚-俯仰-偏航角之所以不呈现时间线性，因为它们是对线性变化的四元数进行非线性变换的结果。最后两个点之间的不连续性，是因为对于横滚-俯仰一偏航角，其最终姿态是一个奇异点。

然而，平移运动在第一个和最后一个点上的速度和加速度是不连续的。问题在于虽然轨迹在空间中是平滑的，但沿轨迹的步距 $s$ 在时间上并不平滑。路径起点上的速度值从零跳跃到有限值，然后在终点又突降至零——没有相应的起始加速和结束减速。我们可以用前面讨论过的标量函数tpoly和lspb来创建一个时间上平滑的 $s$，这样沿路径的运动也平滑了。我们只需将传递给trinterp的第三个参数更改为一个沿路径的单位化距离向量即可：

>> Ts = trinterp(T0, T1, lspb(0, 1, 50))

这样做对于轨迹是不变的，但这时坐标系会沿路径逐渐加速到一个恒定速度，然后结束时再减速，这一点可以从下图中轨迹姿态部分较光滑的曲线反映出来。

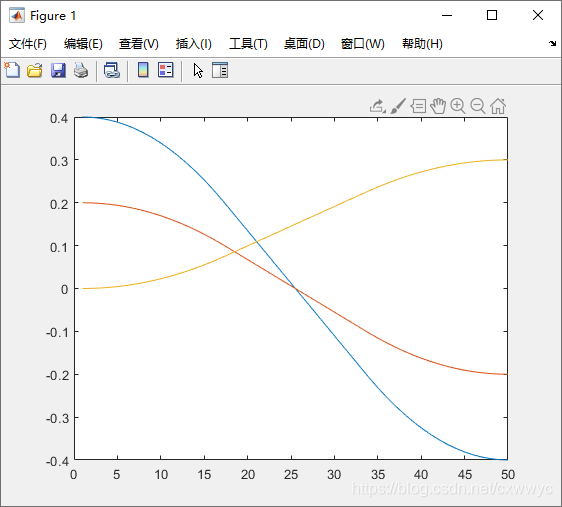
工具箱中还提供了一个方便的速记函数ctraj来进行轨迹插值，其中的参数是初始和最终的位姿，以及分步数量。：

>> Ts = ctraj(T0, T1, 50);