点由坐标系的坐标向量表示。一个刚体上的一组点可以用一个坐标系描述,而且其组成点可由相对于刚体坐标系的位移表示。任何坐标系相对于另一个坐标系的位置和方向,可用相对位姿 表示。相对位姿可以按顺序组合(合成或复合),并且我们还演示了相对位姿如何进行代数运算的操作方法。一个重要的代数运算法则是运算变量不可交换——相对位姿组合的顺序不可交换。
我们已经在二维和三维的情况下探讨过用正交旋转矩阵表示姿态,并用它的延伸——齐次变换矩阵表示姿态和平移。三维下的旋转微妙且复杂,我们也看过其他表示方法,如欧拉角、横滚-俯仰-偏航角和四元数。这些数学对象中,一些本身就被MATLAB支持,而另外一些需要通过机器人工具箱的函数或类才被支持。
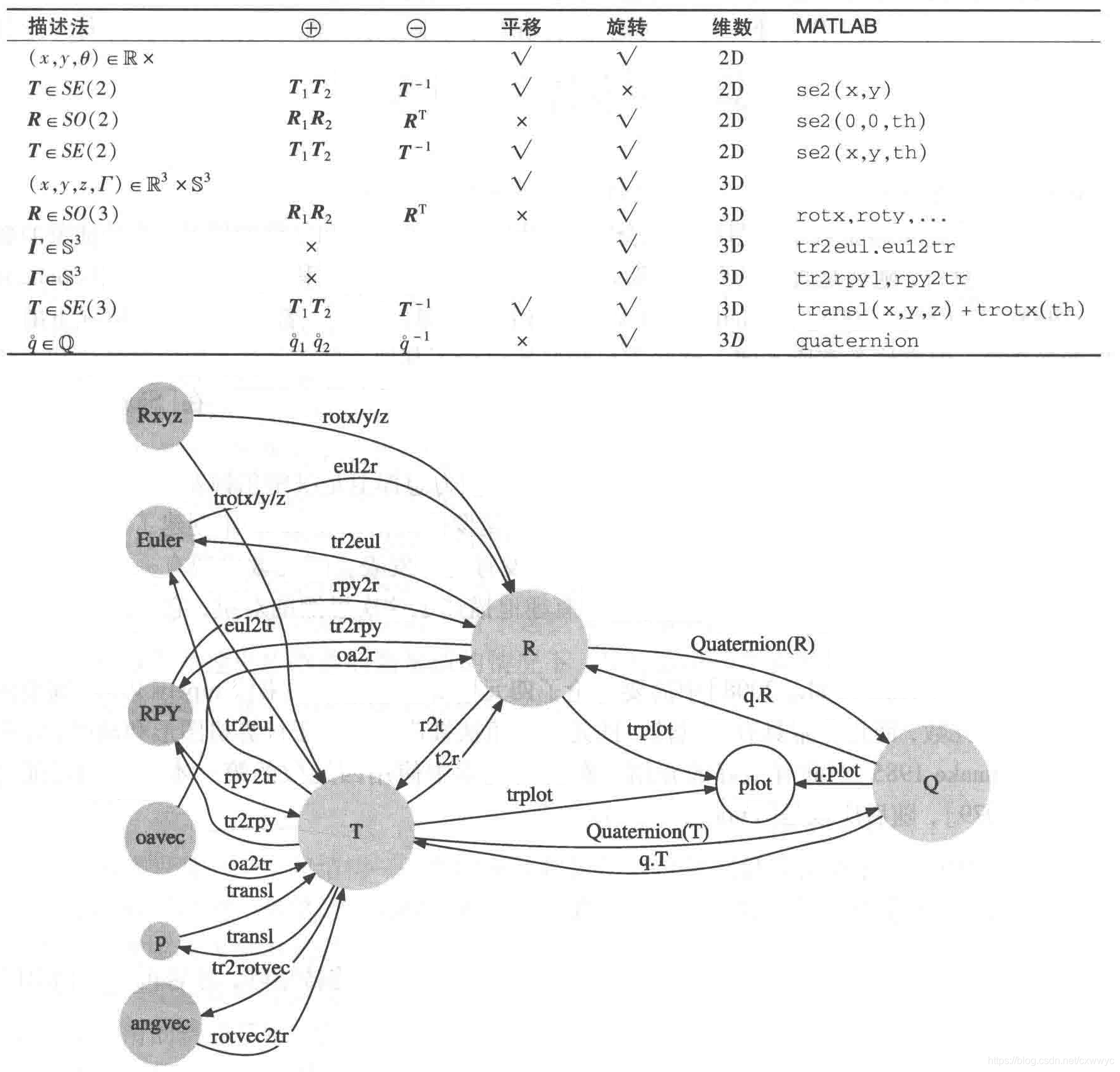
两个重要的经验。第一个是有许多数学对象都可以用来描述位姿,并在表中做出了总结。无所谓好坏,每种方法都有它的长处和短处,我们只需根据手头上要解决的问题选择适合的方法。有时候我们想要一种向量式的描述法,这种情况下 或 就比较适用,但这种描述不能简单地进行复合。有时我们只需要描述三维旋转,这种情况下用 或 就更合适。本书工具箱支持许多不同表示法之间的转换,如图所示。在一般情况下,主要使用齐次变换的方法。
第二个经验是:坐标系很重要。在许多视觉和机器人问题中,必不可少的第一步是给所有的对象分配坐标系,然后以有向图的形式标明相对位姿,并写出位姿的环路方程。这篇文档教你如何用纸建立一个坐标系,它可以拿在手上移动和旋转,使这些思路更直观。