构建乘积数组

题目

　　给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。

思路

　　把B[i]=A[0]*A[1]*.....*A[i-1]*A[i+1]*.....*A[n-1]。看成A[0]*A[1]*.....*A[i-1]和A[i+1]*.....A[n-2]*A[n-1]两部分的乘积。

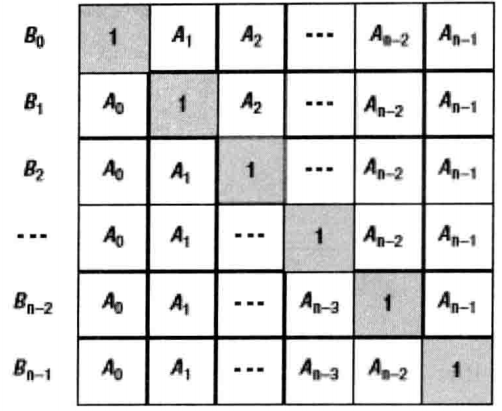
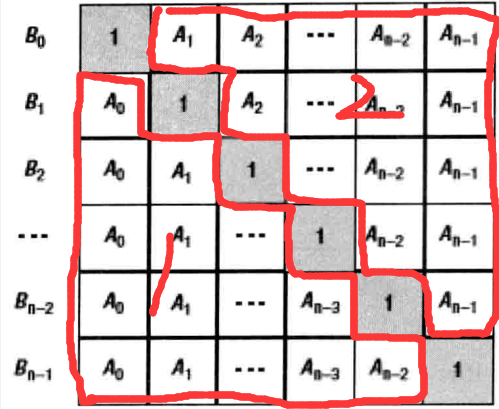
　　不妨设定C[i]=A[0]*A[1]*...*A[i-1]，D[i]=A[i+1]*...*A[n-2]*A[n-1]。C[i]可以用自上而下的顺序计算出来，即C[i]=C[i-1]*A[i-1]。类似的，D[i]可以用自下而上的顺序计算出来，即D[i]=D[i+1]*A[i+1]。

class Solution {
public:
    vector<int> multiply(const vector<int>& A) {
        if(A.size()==0)
            return {};
        
        vector<int> res(A.size(),0);
        res[0]=1;
        for(int i=1;i<A.size();++i)
            res[i]=res[i-1]*A[i-1];
        int tmp=1;
        for(int i=A.size()-2;i>=0;--i)
        {
            tmp*=A[i+1];
            res[i]*=tmp;
        }
        return res;
    }
};