题意略。
思路:
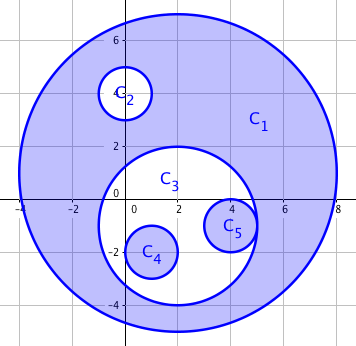
由于不重合这个性质,我们可以将每一个堆叠的圆圈单独拿出来考虑,而不用去考虑其他并列在同一层的存在,
在贪心解法下,发现,被嵌套了偶数层的圆圈永远是要被减去的,而奇数层的圆圈是要加上的。
详见代码:
#include<bits/stdc++.h> #define maxn 1005 #define eps 1e-8 #define pi acos(-1.0) using namespace std; struct Circle{ double x,y,r; Circle(double a = 0,double b = 0,double c = 0){ x = a,y = b,r = c; } double area(){ return r * r * pi; } }; Circle store[maxn]; int mark[maxn]; int n; double dist(int c1,int c2){ double x1 = store[c1].x,y1 = store[c1].y; double x2 = store[c2].x,y2 = store[c2].y; double dx = x1 - x2,dy = y1 - y2; return sqrt(dx * dx + dy * dy); } int sgn(double x,double y){ if(fabs(x - y) < eps) return 0; else if(x > y + eps) return 1; else return -1; } bool in(int x,int y){ double r = fabs(store[x].r - store[y].r); double d = dist(x,y); if(sgn(d,r) <= 0) return true; return false; } bool cmp(const Circle& c1,const Circle& c2){ return c1.r > c2.r; } int main(){ scanf("%d",&n); for(int i = 0;i < n;++i){ scanf("%lf%lf%lf",&store[i].x,&store[i].y,&store[i].r); } sort(store,store + n,cmp); for(int i = 0;i < n;++i){ int cnt = 0; for(int j = 0;j < i;++j){ if(in(i,j)) ++cnt; } mark[i] = cnt; } double ans = 0; for(int i = 0;i < n;++i){ if(mark[i] == 0) ans += store[i].area(); else if(mark[i] & 1) ans += store[i].area(); else ans -= store[i].area(); } printf("%.9lf ",ans); return 0; }