螺旋折线(18JB-7-19')
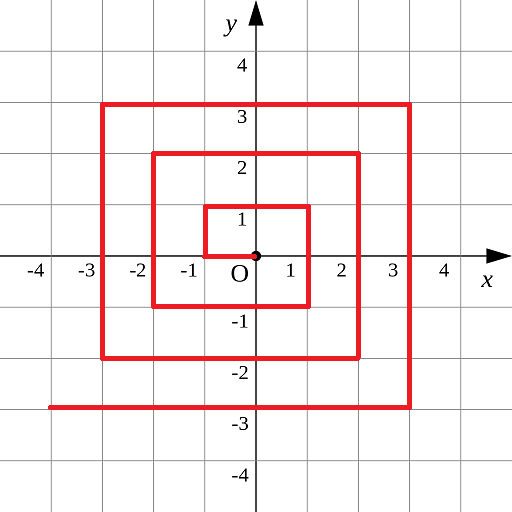
如图p1.pgn所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
【输入格式】
X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
【输出格式】
输出dis(X, Y)
【输入样例】
0 1
【输出样例】
3
资源约定:
峰值内存消耗(含虚拟机)< 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
测试数据
| 测试数据1 | 测试数据2 |
|---|---|
| -466 371 | 36021473 676764583 |
| 测试结果1 | 测试结果2 |
| 867597 | 1832041202571912446 |
package bb;
import java.util.Scanner;
class JB18_7螺旋折线 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long x = sc.nextLong();
long y = sc.nextLong();
sc.close();
// (1)判断所在点所在的正方形:max(|x|,|y|)
long n = Math.max(Math.abs(x), Math.abs(y));
// (2)计算:n之内的正方形的长度之和
// 规律:8,16,24,32,...=>等差数列
// 首项:0(n=1时,内部没有正方形,为0)
// 末项:8*(n-1)(点在n上,内部的正方形为n-1)
// 求和:(0+8(n-1))*n/2=4(n-1)*n
long innerSum = 4 * (n - 1) * n;
// (3)计算:点(x, y)到点(-n, -n)的距离
// 过原点和(-n,-n)画一条辅助线,
// |-线上方的点好算:水平=(x+n),垂直=(y+n)
// |-线下方的点可以折射为线上方的点,用外框正方形的周长去减即可
long sum = 0;
long dis1 = x + n;
long dis2 = y + n;
if (y > x) {
// 线上方的点
sum += (dis1 + dis2);
} else {
// 线下方的点:所在的正方形周长-折射之后的距离
sum += (8 * n - (dis1 + dis2));
}
System.out.println(sum + innerSum);
}
}