算法分析第四次作业

1. 问题

对n个不同的数构成的数组A[1..n]进行排序，其中n=2^k；

2. 解析

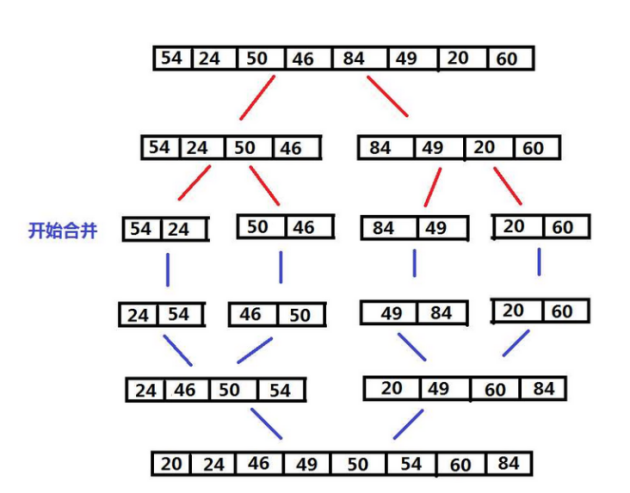
3. 设计

    (1) 将待排序序列从中间一分为二，对左右两边再进行递归分割操作，得到n个相互独立的子序列；

    (2) 对n个独立的子序列递归的执行合并操作，最终得到有序的序列

4. 分析

   

将k=logn和W(1)=0带入得出复杂度为nlogn

5. 源码

    https://github.com/Tinkerllt/algorithm-work.git

#include<stdio.h>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<bitset>
#include<set>
#include<deque>
#include<queue>
#include<vector>
//#include<unordered_map>
#include<map>
#include<stack>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pii pair<int,int>
#define Pii pair<ll,ll>
#define m_p make_pair
#define l_b lower_bound
#define u_b upper_bound 
const int inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;
const int maxn=3e5+11;
const int maxm=2e3+11;
const int mod=1e9+7; 
const double eps=1e-5;
ll rd(){ll x = 0, f = 1; char ch = getchar();while (ch<'0' || ch>'9') { if (ch == '-')f = -1; ch = getchar(); }while (ch >= '0'&&ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }return x * f;}
inline ll qpow(ll a,ll b,ll p){ll res=1;while(b){if(b&1){res*=a;res%=p;}b>>=1;a=a*a%p;}return res;}
inline ll gcd(ll a,ll b){if(b==0) return a;return gcd(b,a%b);}
//iterator 
//head
//priority_queue
void merge(int *data,int start,int end,int *result)
{
    int left_length = (end - start + 1) / 2 + 1;//左部分区间的数据元素的个数
    int left_index = start;
    int right_index = start + left_length;
    int result_index = start;
    while(left_index < start + left_length && right_index < end+1)
    {
        //对分别已经排好序的左区间和右区间进行合并
        if(data[left_index] <= data[right_index])
            result[result_index++] = data[left_index++];
        else
            result[result_index++] = data[right_index++];
    }
    while(left_index < start + left_length)
        result[result_index++] = data[left_index++];
    while(right_index < end+1)
        result[result_index++] = data[right_index++];
}
void merge_sort(int *data, int start, int end, int *result)
{
    if(1 == end - start)//如果区间中只有两个元素，则对这两个元素进行排序
    {
        if(data[start] > data[end])
        {
            int temp  = data[start];
            data[start] = data[end];
            data[end] = temp;
        }
        return;
    }
    else if(0 == end - start)//如果只有一个元素，则不用排序
        return;
    else
    {
        //继续划分子区间，分别对左右子区间进行排序
        merge_sort(data,start,(end-start+1)/2+start,result);
        merge_sort(data,(end-start+1)/2+start+1,end,result);
        //开始归并已经排好序的start到end之间的数据
        merge(data,start,end,result);
        //把排序后的区间数据复制到原始数据中去
        for(int i = start;i <= end;++i)
            data[i] = result[i];
    }
}
int main(){
    //std::ios::sync_with_stdio(false);
    int n=rd();
    int data[100];
    int result[100];
    for(int i=0;i<n;i++){
        data[i]=rd();
    }
    cout << "Before sorted:" << endl;
    for(int i = 0;i < n;++i)
        cout << data[i] << "  ";
    cout << endl;
    cout << "After sorted:" << endl;
    merge_sort(data,0,n-1,result);
    for(int i = 0;i < n;++i)
        cout << data[i] << "  ";
    cout << endl;
}