Codeforces-Round#569 Div.2

前面考试周，抱歉拖了这么久。

A题 Alex and a Rhombus

基本思路

递推解决，n=1时，Count(1)=1；n>1时，Count(n)=Count(n-1)+（n-1）*4

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int n;cin>>n;
	long long res=1;
	for(int i=1;i<=n;i++)
	{
		res+=4*(i-1);
	}
	cout<<res;
	return 0;
 } 

B题 Nick and Array

基本思路

按绝对值，负数>正数，因此只要把所有的数转成负数,若n被2整除，则结果为正，若n%2余1，则将最小的负数转成正数。

注意题目要求按顺序输出

#include<bits/stdc++.h>
using namespace std;
int num[100005];
int MINN = 99999,pos=0;
int main()
{
	int n,ncount=0;cin>>n;
	for(int i=0;i<n;i++)
	{
		cin >> num[i];
		if(num[i]>=0)
			num[i] = -num[i] - 1;
		if(num[i]<=MINN&&num[i]!=-1) 
		{
			pos=i;
			MINN=num[i];
		}
	}
	if(n%2!=0)
	{
		num[pos]=-num[pos]-1;
	}
	for(int i=0;i<n;i++)
	{
		cout<<num[i]<<" ";
	}
	return 0;
}

C题

基本思路

当双端队列q[0]为最大值时会陷入循环，因此，需要递推的步数不超过(10^5)，后面可以用模数组下标来选择输出的第二个数。（记得先pop_front再模n-1）

#include<bits/stdc++.h>
#include<deque>
using namespace std;
struct{
	int a,b;
}qu[100010];
int main()
{
	deque<int>q;int n,query,maxn=-99999;
	cin>>n>>query;
	for(int i=0;i<n;i++)
	{
		int num;cin>>num;
		q.push_back(num);
		maxn=max(maxn,num);
	}
	long long cnt=0;
	while(q.front()!=maxn)
	{
		cnt++;
		int n1=q.front();
		q.pop_front();int n2=q.front();q.pop_front();

		q.push_front(max(n1,n2));
		q.push_back(min(n1,n2));
		qu[cnt].a=n1;qu[cnt].b=n2;
	}
	q.pop_front();
	for(int i=0;i<query;i++)
	{
		long long m;
		cin>>m;
		if(m<=cnt)
		{
			cout<<qu[m].a<<" "<<qu[m].b<<endl;
		}
		else
		{
			int pos=(m-cnt-1)%(n-1);
			cout<<maxn<<" "<<q[pos]<<endl;
		}
	}
	return 0;
}

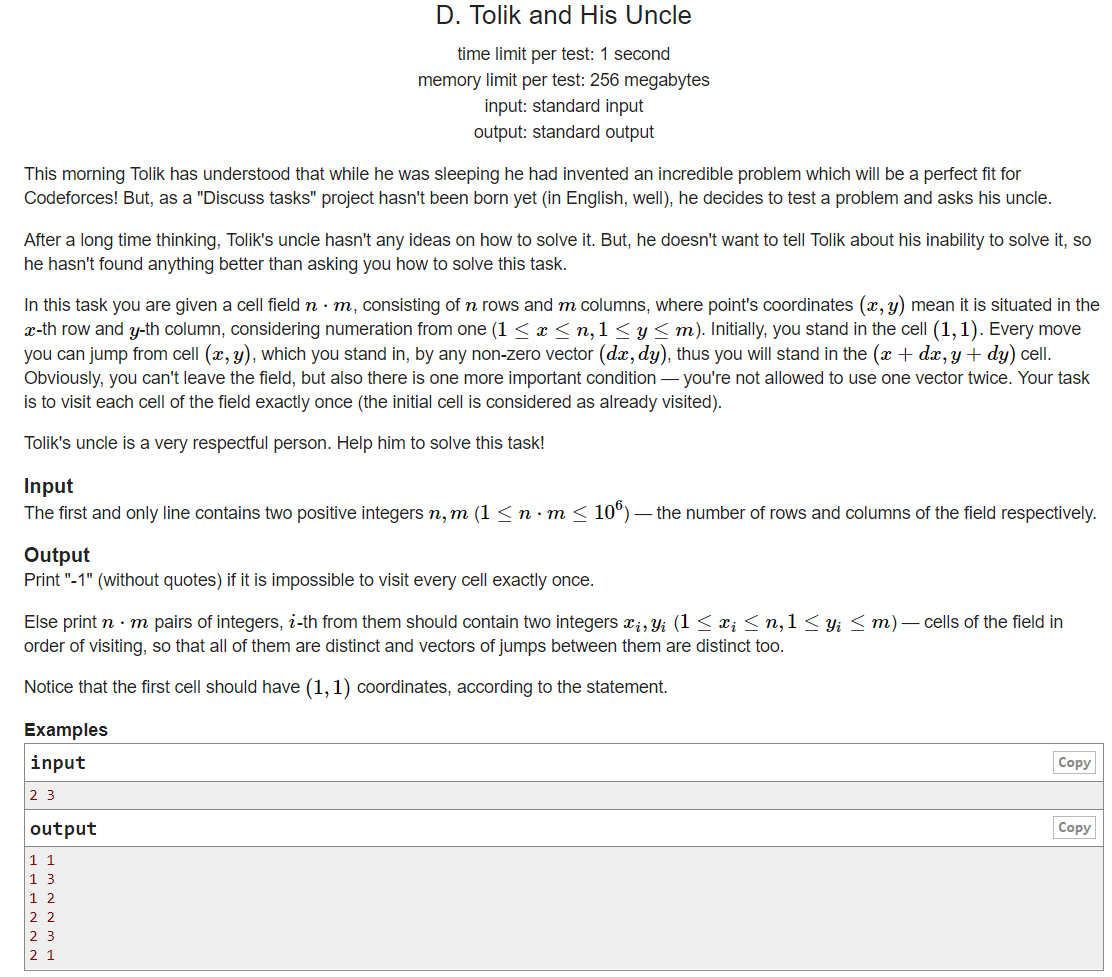
D题 Tolik and His Uncle

基本思路：

采用对称的思想走，路径就不会重复，假设棋盘为N*M，第一次从（1,1）_{>（n,m），第二次从（n,m）}>（1,2），以此类推。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(NULL);
	int m,n;
	cin>>n>>m;
	for(int i=1;i<=n/2;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cout<<i<< ' '<<j<<'
';
			cout << n-i+1 << ' ' << m-j+1 << '
'; 
		}
	}
	if(n%2){
		for(int i = 1;i <= m/2;i++){
			cout << n/2+1 << ' ' << i << '
';
			cout << n/2+1 << ' ' << m-i+1 << '
';
		}
		if(m%2){
			cout << n/2+1 << ' ' << m/2+1 << '
';
		}
	}
	return 0;
} 

E题 Serge and Dining Room

基本思路：

采用线段树区间前缀和思想实现查询和修改，建立一个节点包含两组信息：菜肴价格和学生的钱数

//E_std.cpp
#include<bits/stdc++.h>
#define clr(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn=1000010;
int n,m,q;
int sum[maxn<<2],maxx[maxn<<2];
int a[maxn],b[maxn];
void update(int o,int l,int r,int p,int val){
    if(l==r){
        sum[o]+=val;
        maxx[o]+=val;
        return;
    }
    int mid=(l+r)>>1;
    if(p<=mid)update(o<<1,l,mid,p,val);
    else update(o<<1|1,mid+1,r,p,val);
    sum[o]=sum[o<<1]+sum[o<<1|1];
    maxx[o]=max(maxx[o<<1|1],maxx[o<<1]+sum[o<<1|1]);
    //这里的每一个maxx，都是对应的 区间最大后缀和  但不是整根数轴的最大后缀和。 
}
struct node{
    int max,sum;
};
int query(int o,int l,int r,node tep){
    if(l==r){
        return l;
    }
    int mid=(l+r)>>1;
    node tep2;
    tep2.sum=tep.sum+sum[o<<1|1];
    tep2.max=maxx[o<<1|1]+tep.sum;//将 标号为o这段区间的后面一段（o+1）的影响合并到o区间中 
    if(tep2.max>0){
        return query(o<<1|1,mid+1,r,tep);
    }
    else {
        return query(o<<1,l,mid,tep2);
    }
}
int main(){
    while(cin>>n>>m){
        clr(sum,0),clr(maxx,0);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            update(1,1,maxn-1,a[i],1);
        }
        for(int i=1;i<=m;i++){
            scanf("%d",&b[i]);
            update(1,1,maxn-1,b[i],-1);
        }
        cin>>q;
        while(q--){
            int op,pos,val;
            scanf("%d%d%d",&op,&pos,&val);
            if(op==1){
                update(1,1,maxn-1,a[pos],-1);
                update(1,1,maxn-1,a[pos]=val,1);
            }else{
                update(1,1,maxn-1,b[pos],1);
                update(1,1,maxn-1,b[pos]=val,-1);
            }
            
            if(maxx[1]<=0)puts("-1");
            else printf("%d
",query(1,1,maxn-1,{0,0}));

        }
    }
}