洛谷P3386二分图匹配

原题链接

二分图的性质

定理：当且仅当无向图G的每一个回路的次数均是偶数时，G才是一个二分图。如果无回路，相当于任一回路的次数为0，故也视为二分图。

二分图的判定

如果一个图是连通的，可以用如下的方法判定是否是二分图：
在图中任选一顶点v，定义其距离标号为0，然后把它的邻接点的距离标号均设为1，接着把所有标号为1的邻接点均标号为2（如果该点未标号的话），如图所示，以此类推。
标号过程可以用一次BFS实现。标号后，所有标号为奇数的点归为X部，标号为偶数的点归为Y部。
接下来，二分图的判定就是依次检查每条边，看两个端点是否是一个在X部，一个在Y部。
如果一个图不连通，则在每个连通块中作判定。

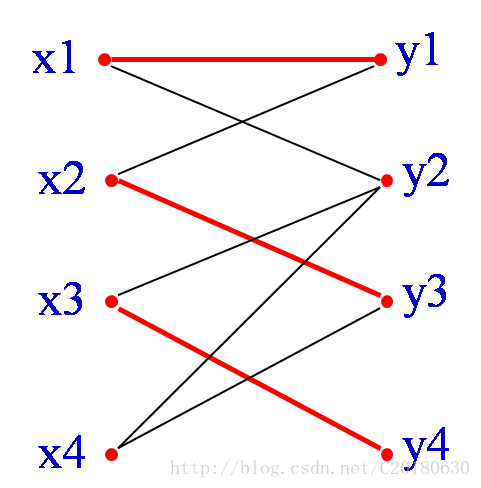
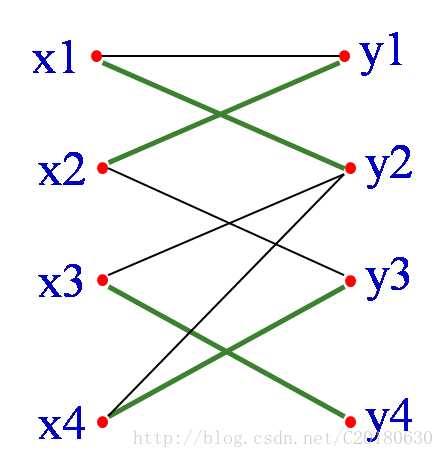
增广路。

如果你仔细读过并画过图，不难发现如果找到一条增广路，那么配对的个数就会加1。 所以说，增广路的本质其实就是一条路径的起点和终点都未配对的点的边。

---

匈牙利算法：

这个叫匈牙利算法(Hungarian method)的东西是由匈牙利数学家Edmonds于1965年提出，所以叫匈牙利算法。匈牙利算法是二分图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

复杂度：

时间复杂度 : 邻接矩阵最坏为O(n3)
邻接表： O(mn)
空间复杂度 : 邻接矩阵：O(n2)
邻接表： O(n+m)

另一个重要概念：二分图

二分图是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集，则称图G为一个二分图。

简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。满足这样的图就叫二分图。

但我们怎么判断一个图是不是二分图？？？

其实也不难，用红蓝点的方法就行。首先讲任意的一个顶点染成红色，再把这个点相邻的顶点染成蓝色，如果按照这种染色方式可以将所有的顶点全部着色，并且相邻的顶点的颜色不同，那么该图就是一个二分图。

#define MAXV 1000//这里应该根据题目自定

vector<int> G[MAXV];  //图 
int V;                       //顶点数 
int color[MAXV];  //顶点的颜色 （1 or -1） 

//顶点v，颜色c 
bool dfs(int v,int c){
    color[v] = c;
    //把当前顶点相邻的顶点扫一遍 
    for(int i = 0;i < G[v].size(); i++){
        //如果相邻顶点已经被染成同色了,说明不是二分图 
        if(color[G[v][i]] == c) return false;
        //如果相邻顶点没有被染色,染成-c,看相邻顶点是否满足要求 
        if(color[G[v][i]] == 0 && !dfs(G[v][i],-c)) return false;
    }
    //如果都没问题，说明当前顶点能访问到的顶点可以形成二分图 
    return true;
}

void solve(){
    //可能是不连通图，所以每个顶点都要dfs一次 
    for(int i = 0;i < V; i++){
        if(color[i] == 0){
            //第一个点颜色为 1 
            if(!dfs(i,1)){
                cout << "No" << endl;
                return;
            }
        }
    }
}

匈牙利算法

根据上文的描述，既然增广路的作用是“改进匹配方案”（即增加配对数），那么如果我们已经找到了一种匹配方案，不难发现如果在当前匹配方案下再也找不到任何增广路的话，那么当前匹配就是二分图的最大匹配，算法如下。

1.首先从任意的一个未配对的点u开始，从点u的边中任意选一条边（假设这条边是从u->v）开始配对。如果点v未配对，则配对成功，这是便找到了一条增广路。如果点v已经被配对，就去尝试“连锁反应”，如果这时尝试成功，就更新原来的配对关系。
所以这里要用一个matched[v] = u。配对成功就将配对数加1,。

2.如果刚才所选的边配对失败，那就要从点u的边中重新选一条边重新去试。直到点u 配对成功，或尝试过点u的所有边为止。

3.接下来就继续对剩下的未配对过的点一一进行配对，直到所有的点都已经尝试完毕，找不到新的增广路为止。

4.输出配对数。

/*
1）如果后来的和以前的发生矛盾，则以前的优先退让
2）如果以前的退让之后没有cp可处，则以前的拒绝退让，新来的去寻找下一个匹配。
3）如果新来的谁也匹配不上了，那就这么单着吧
*/
#include<bits/stdc++.h>
#define MAXN 1000100
using namespace std;
typedef struct {
    int from,to,next;
    int weight;
}EDGE;
EDGE edges[MAXN];
int head[MAXN],cnt=1;//从第一个点开始访问
int match[MAXN],dfn[MAXN];//匹配数组,时间戳数组
void add(int from ,int to)
{
    edges[cnt].from=from;
    edges[cnt].to=to;
    edges[cnt].next=head[from];
    head[from]=cnt++;
}
bool dfs(int u,int vist)
{
    for(int i=head[u];i;i=edges[i].next)
    {
        if(dfn[edges[i].to]!=vist)
        {//如果本轮未访问
            dfn[edges[i].to]=vist;//标记已访问
            if(!match[edges[i].to]||dfs(match[edges[i].to],vist))
            {//如果有从match出发的增广路径
                match[edges[i].to]=u;return true;
            }
        }
    }
    return false;
}

int main()
{
    int n,m,e;cin>>n>>m>>e;
    int ans=0;
    for(int i=0;i<e;i++)
    {
        int a,b;cin>>a>>b;
        if(a>n||b>m)continue;
        add(a,b);
    }
    for(int i=1;i<=n;i++)
    {
        if(dfs(i,i))ans++;
    }
    cout<<ans<<endl;
    return 0;
}