多元方程求解:无解/有解 -> 唯一解/无穷解
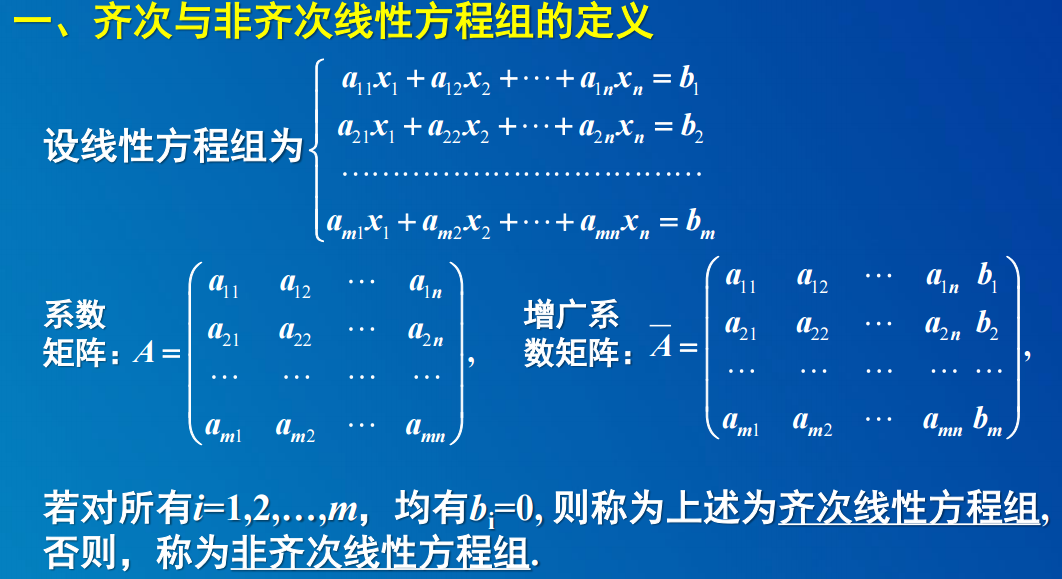
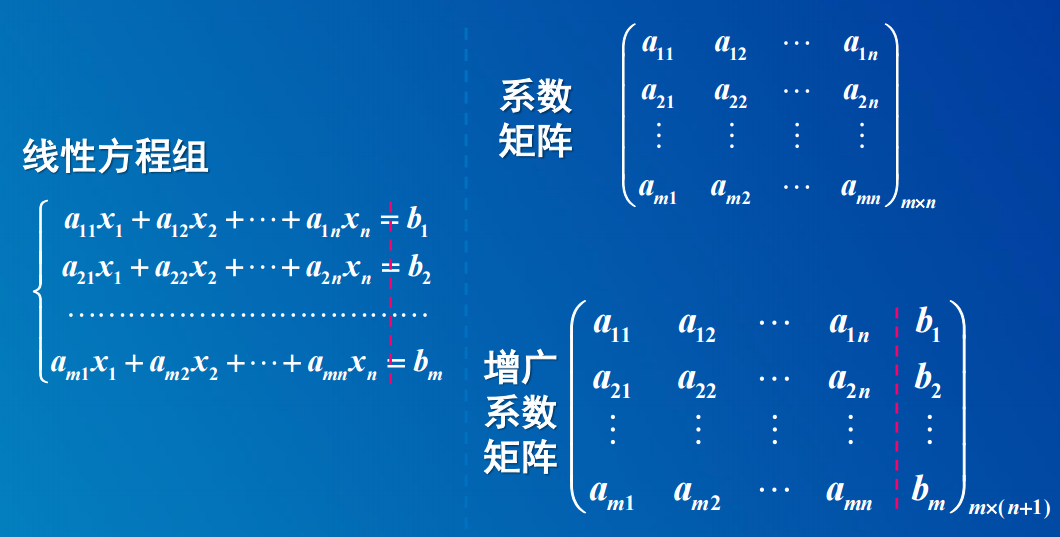
矩阵:由mn个实数排成行列的矩形数表,即称为mXn型的矩阵。(m=n)称为n阶方阵。
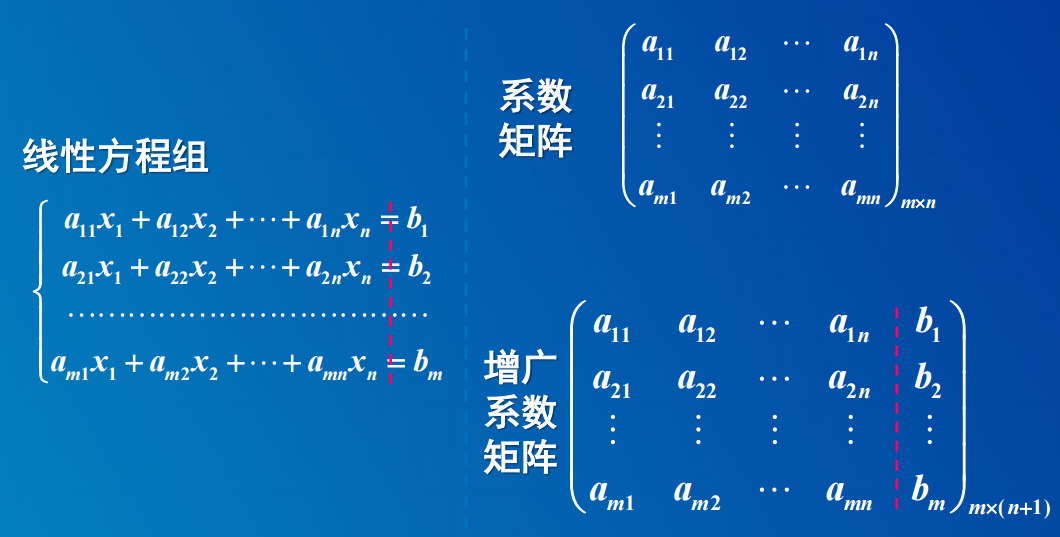
线性方程可分为:系数矩阵和增广矩阵
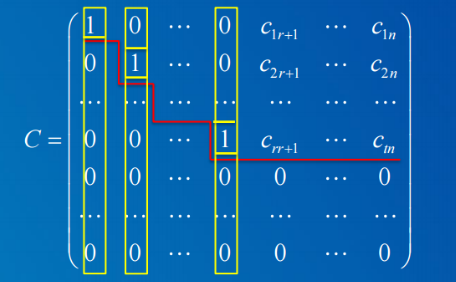
阶梯矩阵:1)矩阵有0行,并一定在矩阵下方,2)对于每个非0行,从左起第一个非0元素为此行的主元。

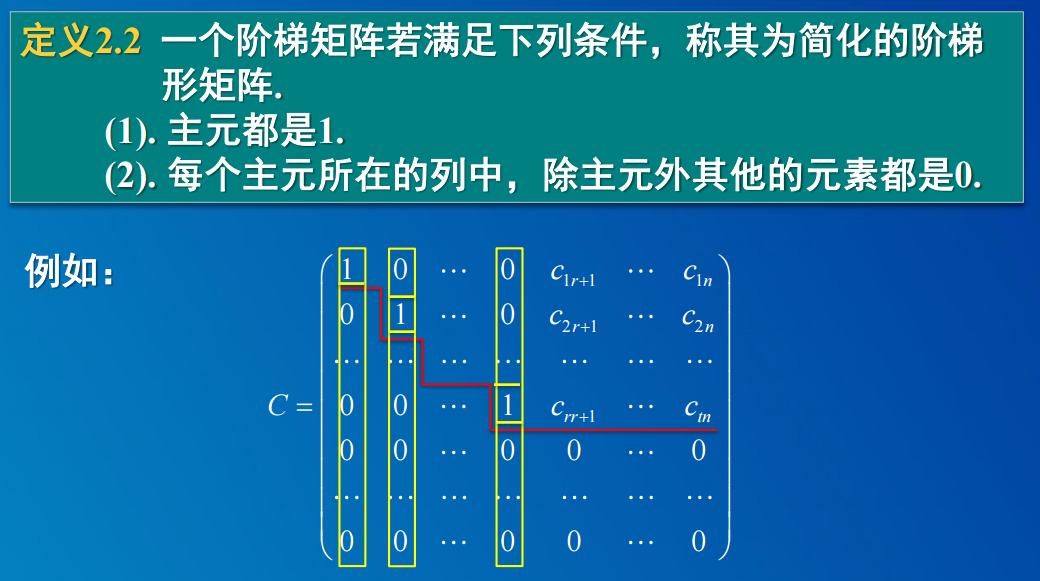
简化的阶梯矩阵:1)主元都是1,2)每行除主元外,都是0。 例如:
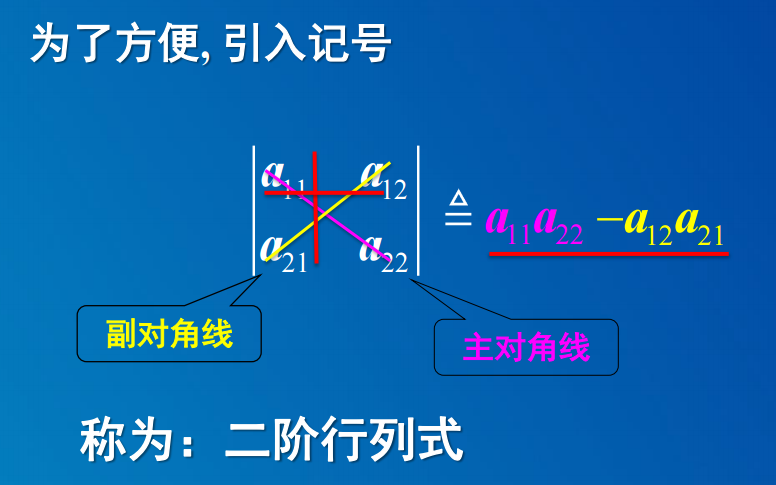
高斯消元法:

齐次方程组:增广矩阵中,bi=0,则为齐次线性方程组,否则,为非齐次线性方程组。

1. 二元、三元一次方程组







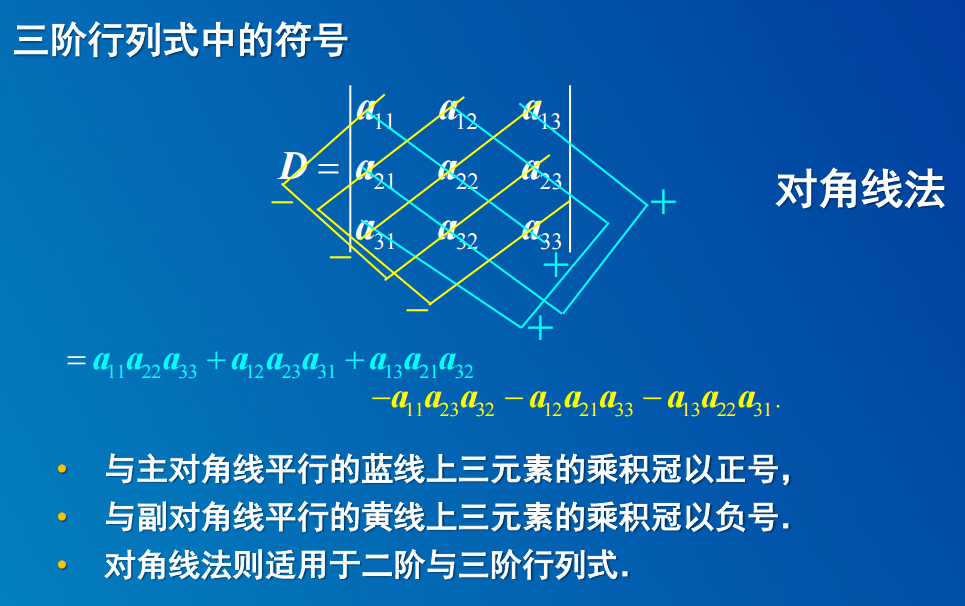

2. 一般线性方程组的解法
求解:是否有解->有几个解
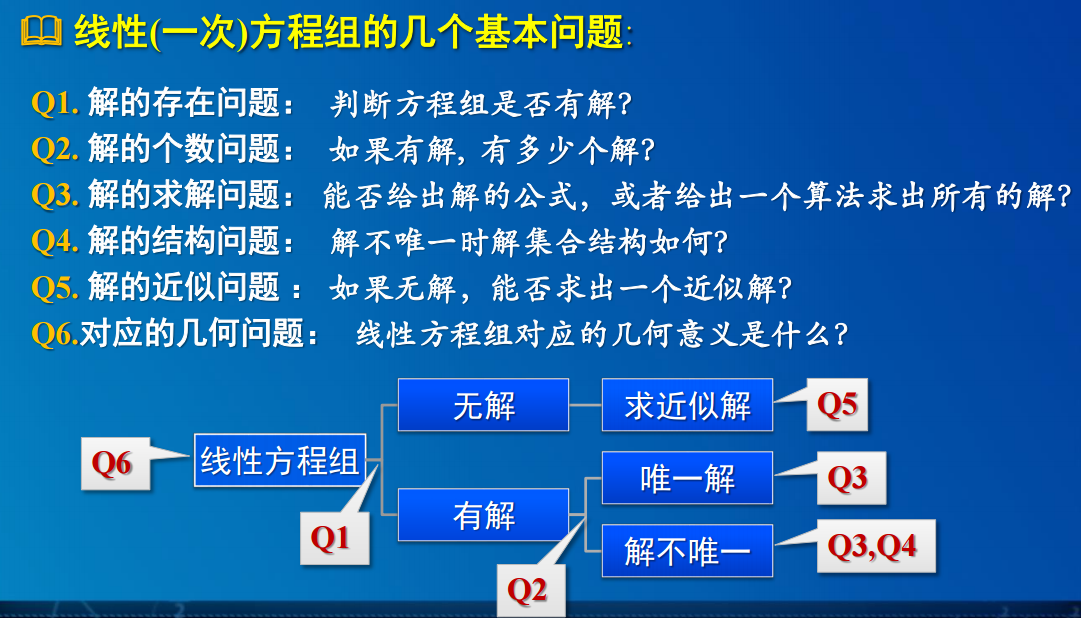







3. 线性方程组解的判定


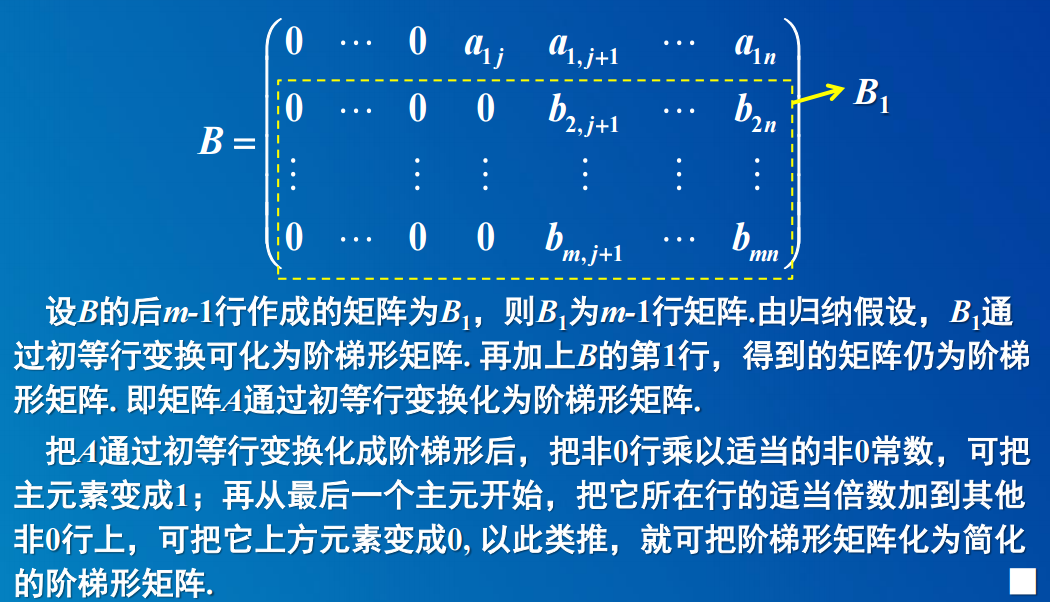

若r=n,说明有唯一解
若r<n,说明有无穷多个解。
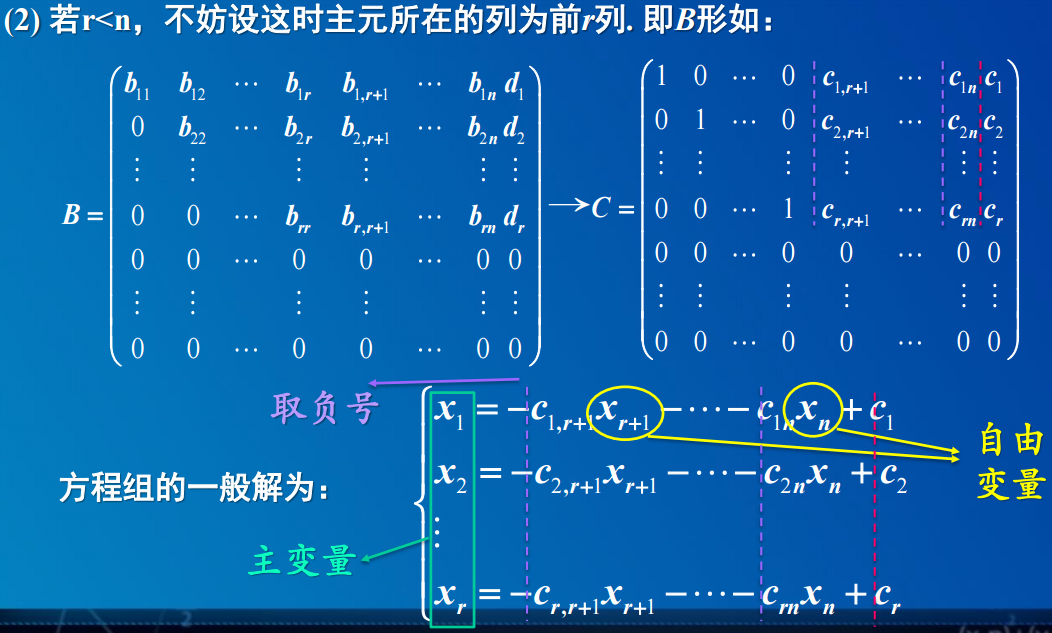
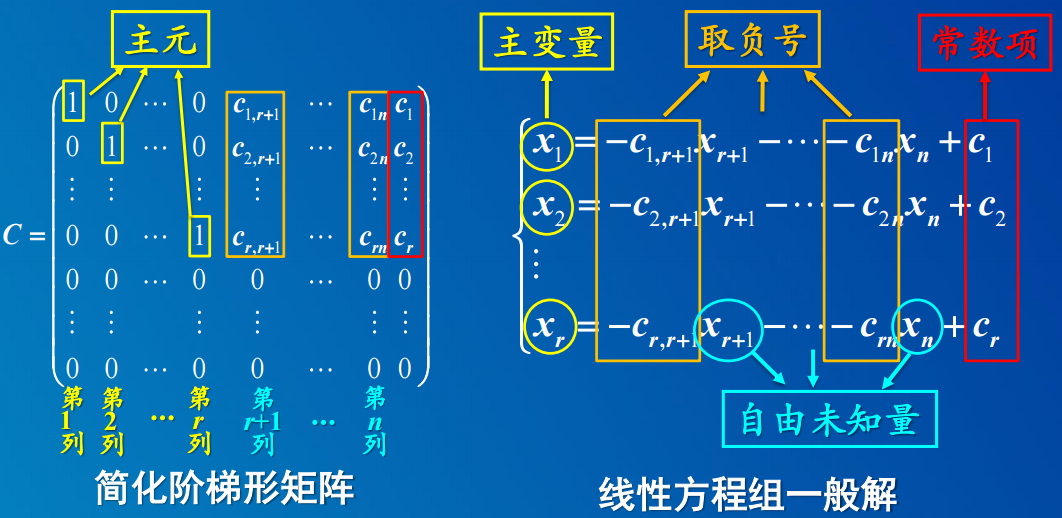
高斯消元法:

4. 齐次方程组