S&P_06_常见随机变量的期望与方差和应用实例

二项分布： E(X) = np, D(X) = np(1-p)

泊松分布： E(X)=λ，D(X)=λ

均匀分布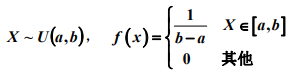： E(X) = (a+b)/2， D(X) = (b-a)^2/12

指数分布： E(X)=1/λ，D(X)=1/λ^2

标准正太分布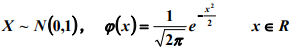： E(X)=0， D(X)=1

期望是随机 变量的中心化特征，是随机分布的平均值。方差是随机变量对期望（平均值）偏离程度的度量。

　　

你首先是已知在每一状态下的取值，以及概率。然后你才能推断出期望。而概率在大多出情况下是由频数近似而来的。
频数就是在事件发生的次数/实验的总次数。在这个定义中，就已经隐藏了大样本的条件了。
因而，期望就是在多次实验之后，你预期的结果。而不是你下一次，或者某次实验的结果。

 

随机变量X函数的数学期望 　　

　　

　　   

  

  

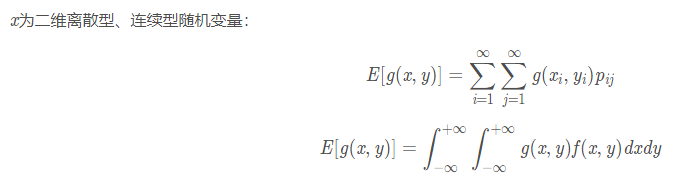
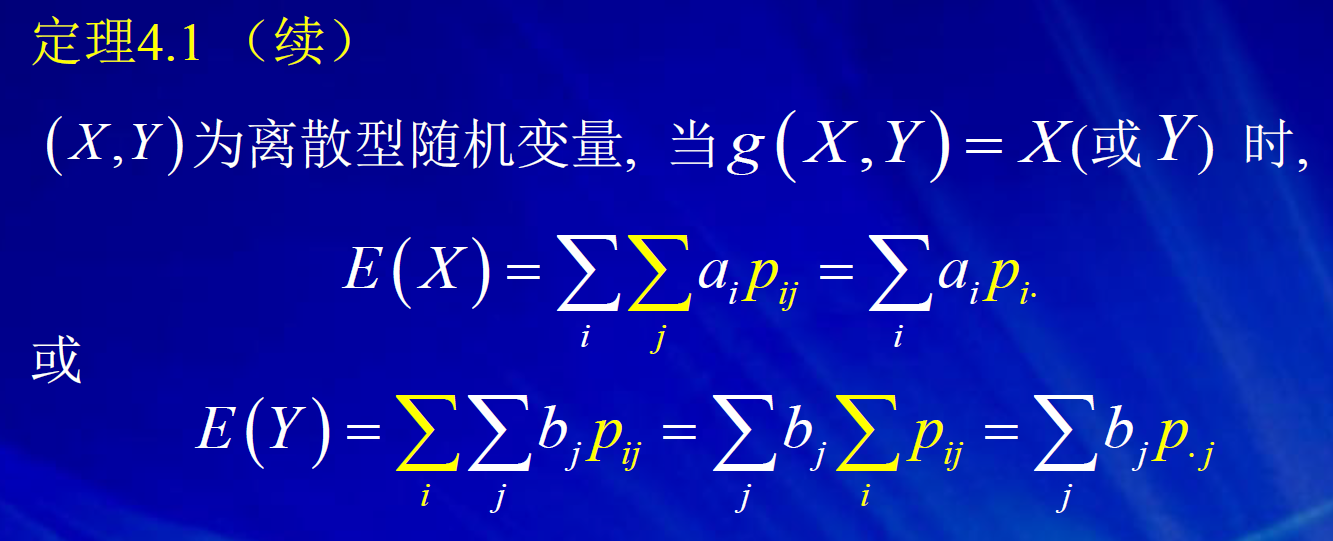
常见的随机变量的期望和方差

1. 二项分布与泊松分布的期望与方差

1.2 二项分布

   

 

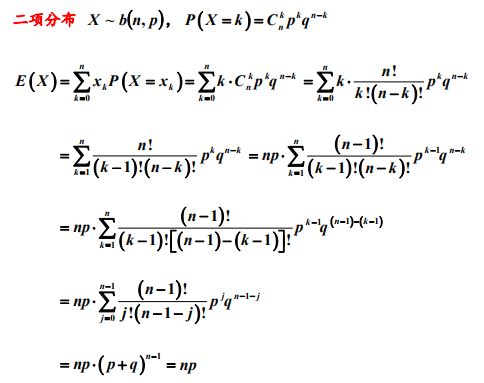
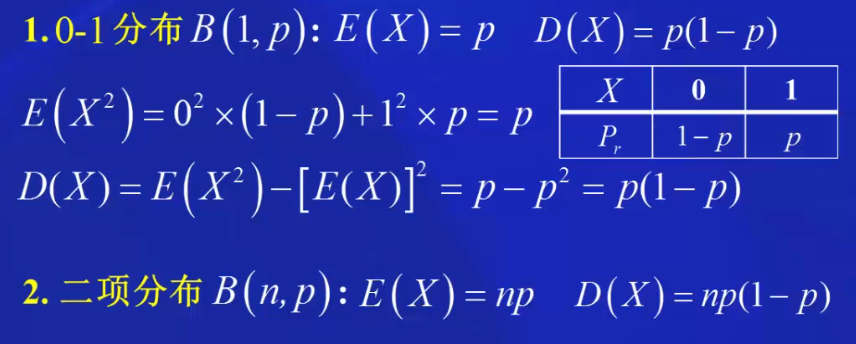
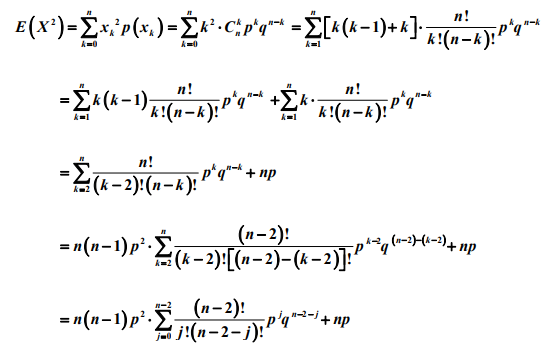
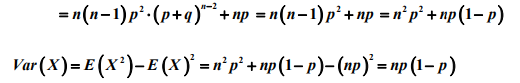
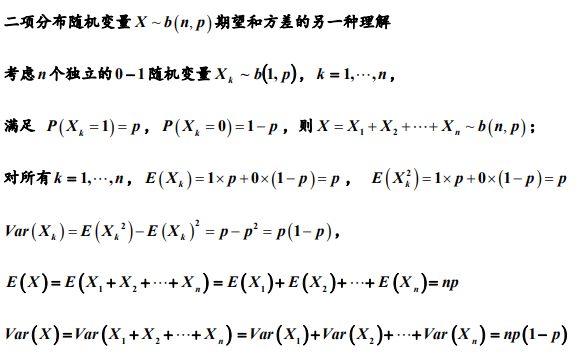
由于Xn是独立事件，所以E(X)=E(X1)+....+E(Xn)=np，且Var(X)=Var(X1)+....+Var(Xn)=np(1-p)

Var(X+Y)=Var(X)+Var(Y)+2E[(X-E(X))(Y-E(Y))]

1.2 泊松分布

  

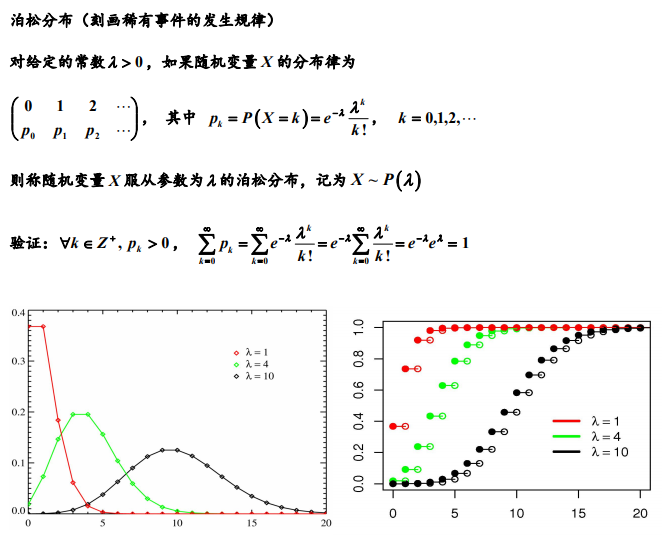
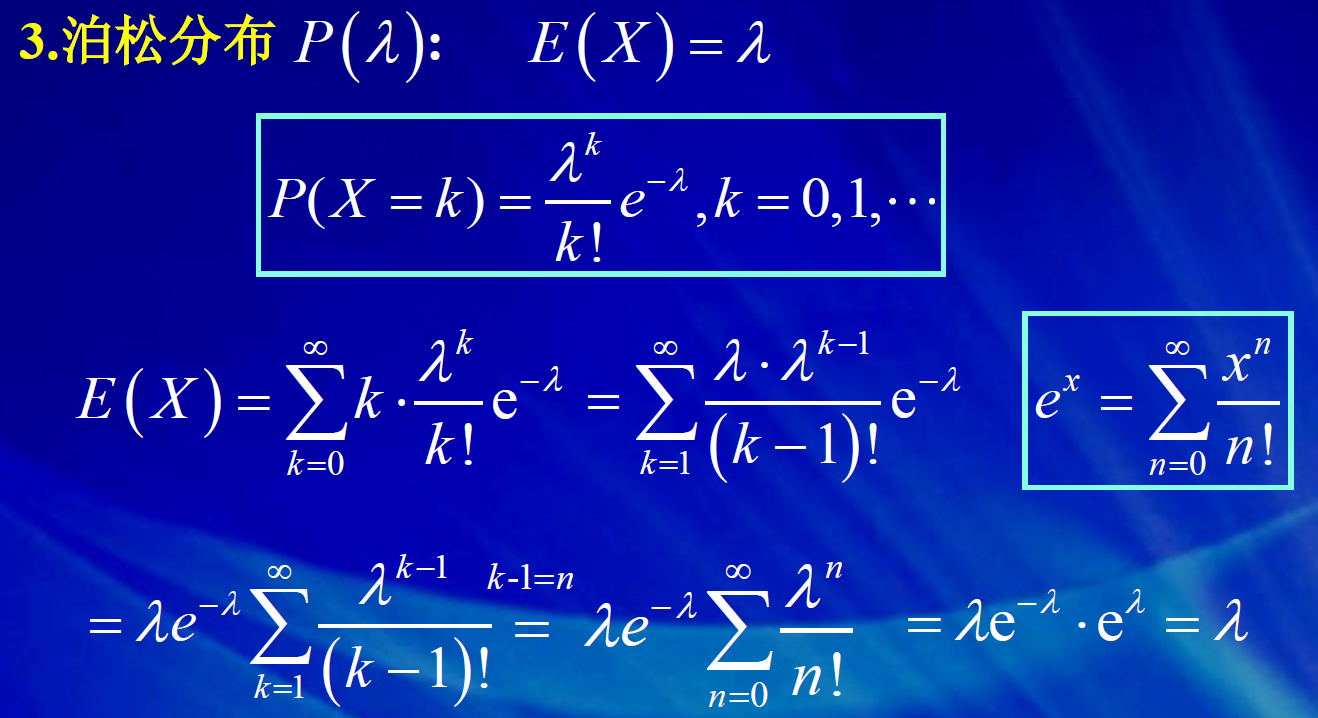
如图给出的是参数1，4，10对应的泊松分布的分布列（左图）和分布函数（右图），可以看出泊松分布的分布列有一个最大值，随着λ的不同，峰值的高度和位置均有不同。达到峰值后，随着k的增大概率值Pk迅速减小。虽然泊松分布的取值范围是全体非负整数，但对较大的K，X=K的概率非常小。

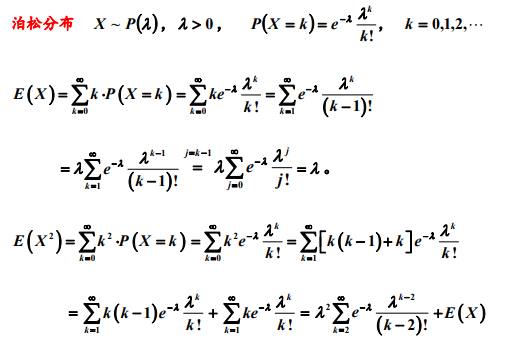
 2. 几何分布的期望和方差

 

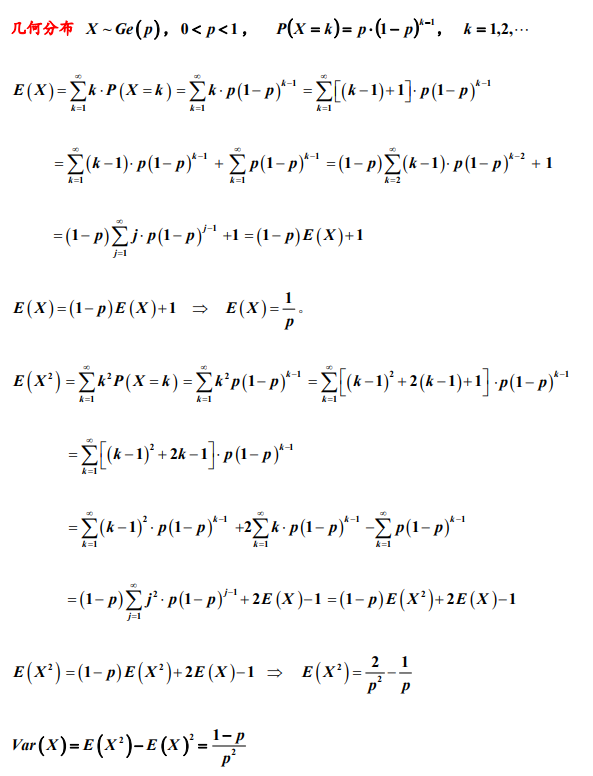
备注：计算泊松分布和几何分布随机变量的期望过程中，做了诸如将k 拆分为(k-1)+1， 以及 2 k 拆分为 k(k-1)+k 或(k-1)^2+2(k-1)+1 等等的等价变形处理，这一类的 拆分是概率统计计算中常用的处理方法，目的是为了凑出随机变量的分布列求和或 期望等的求和式，利用求和式的概率意义和已知的概率结果往往可以简化计算。

3. 均匀、指数和正态分布的期望与方差

   

     

 

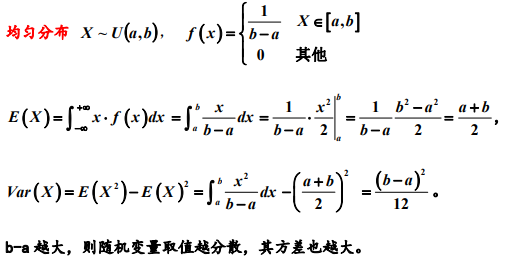
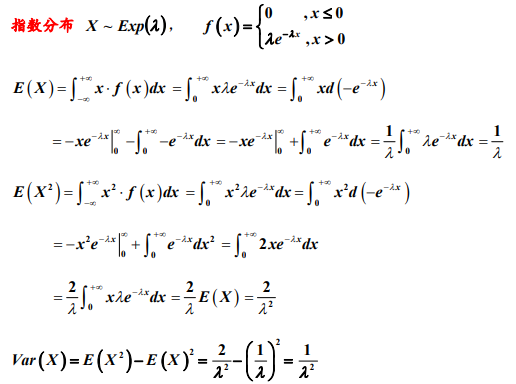
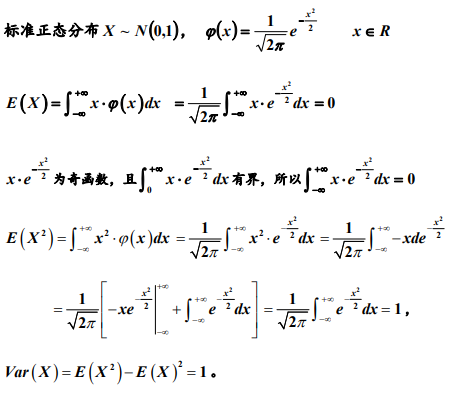
左边积分为奇函数，所以它的积分等于0.

 

 

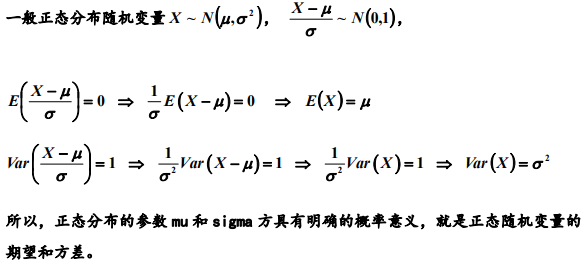
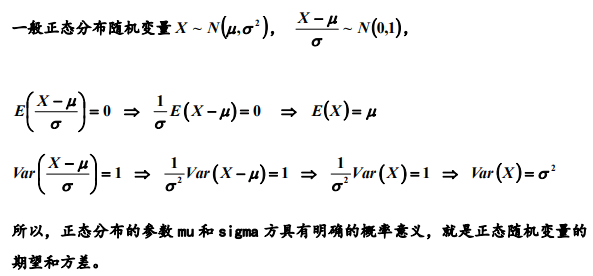
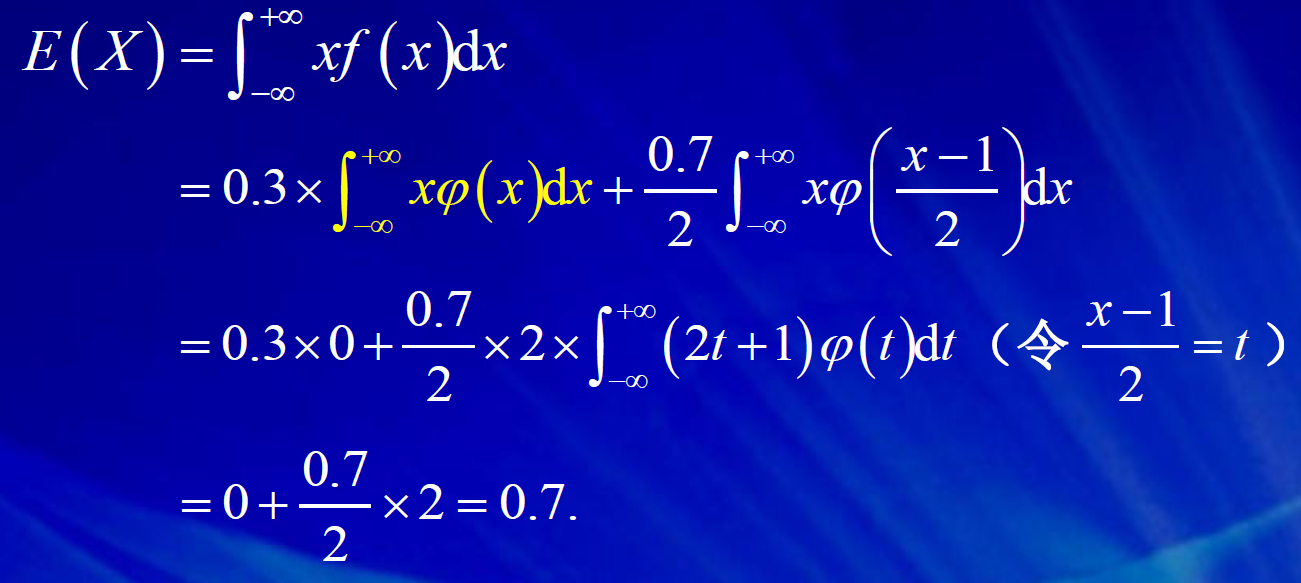
 4. 随机变量函数的期望和方差

  

   

    

    

 

  

  

 

  

 

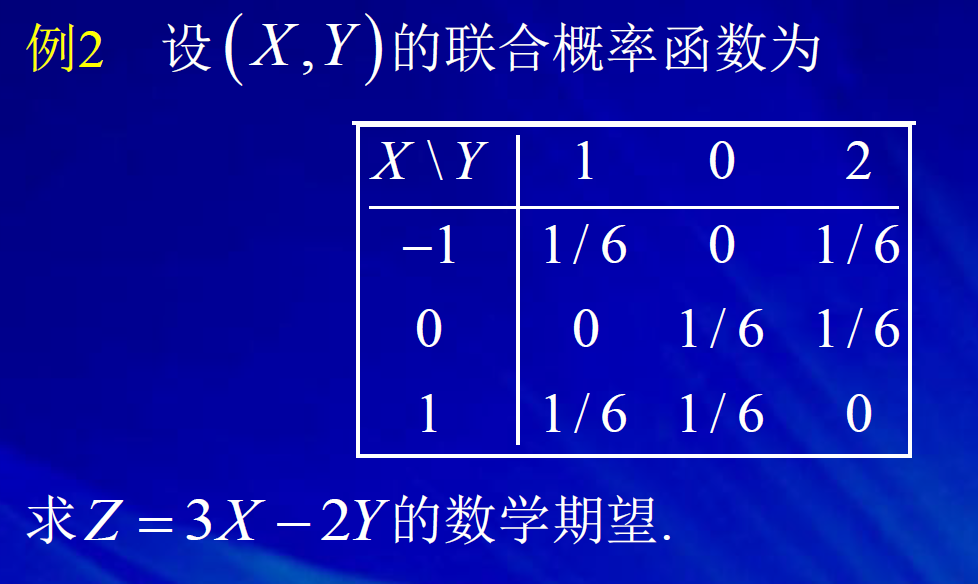
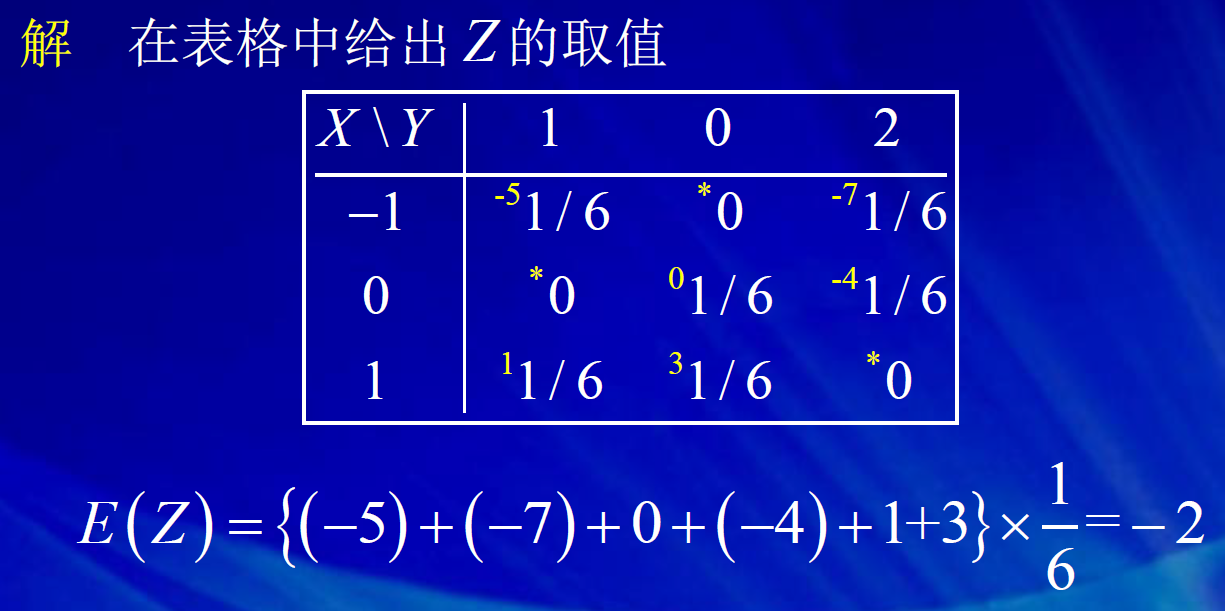
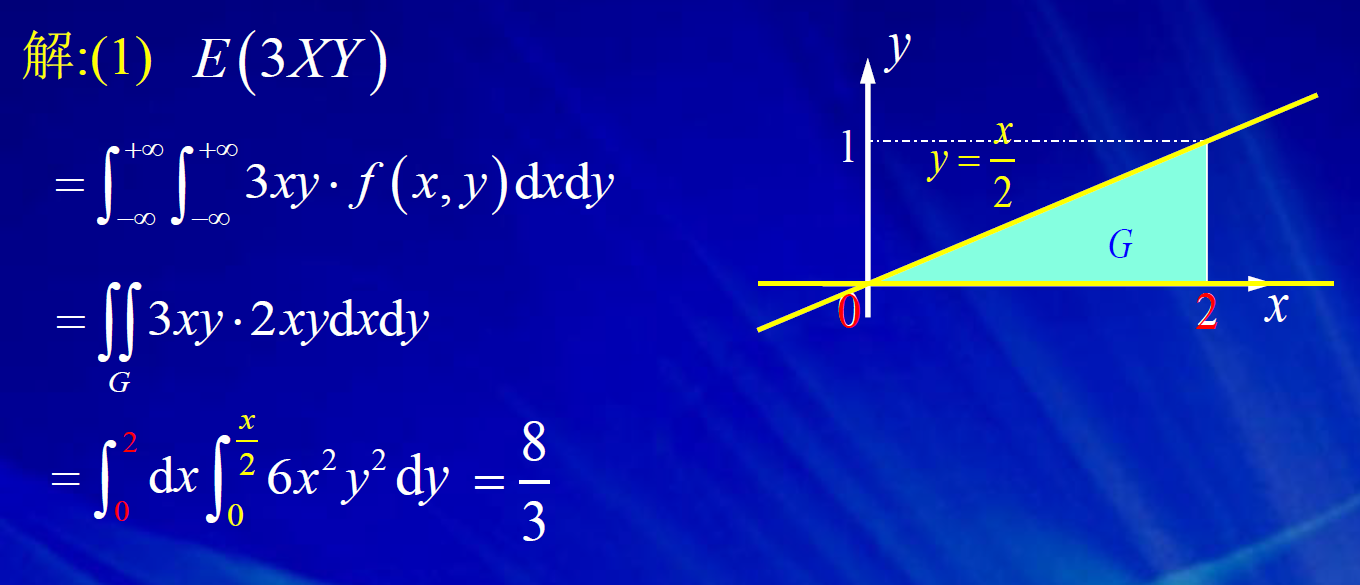
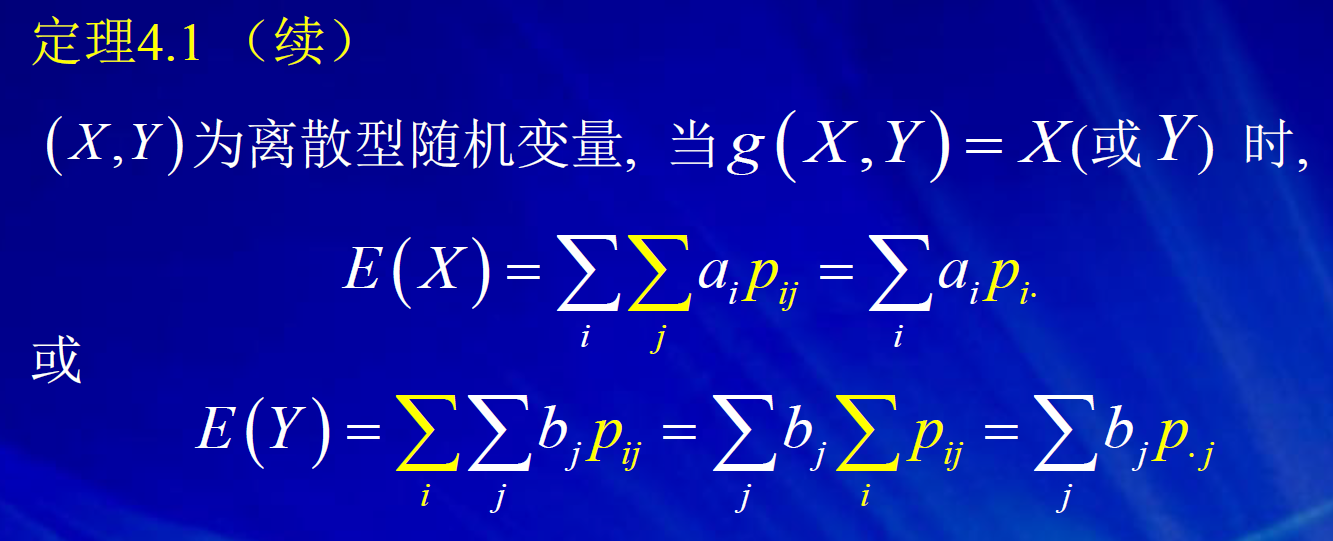
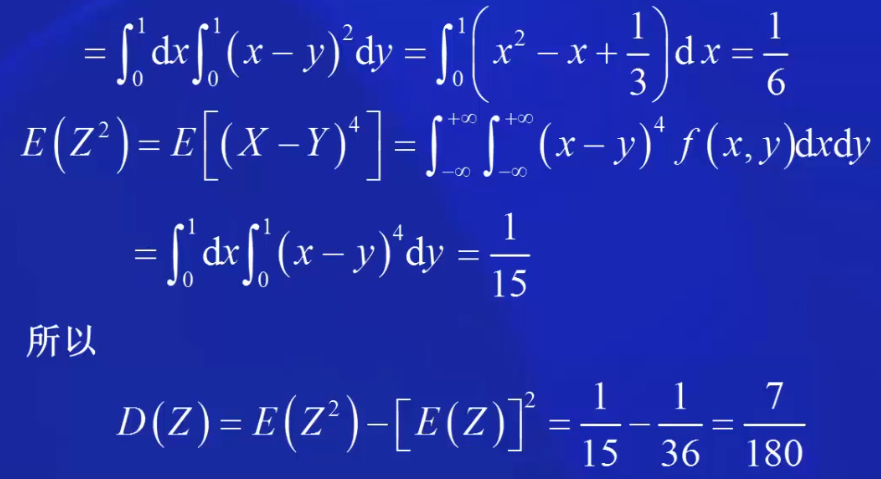
去中心化，只是将x轴的位置进行平移，但曲线的陡峭程度不变。 标准化，是先进行去中心化，然后再标准化。