Lecture 7:The VC Dimension
7.1 Definition of VC Dimension
VC Dimension : The formal name of maximum non-break point
对有的 infinite hypothesis VC 存在 breakpoint K, dvc = K -1。 如果 inputs sample 数不大于 dvc 则能被该 hypothesis shatter。因为 VC Dimension 和 breakpoint 数值上很接近, 关于 VC Dimension 的讨论可以参考第 6 节课。不在此处赘述

图 7-1
7.2 VC Dimension of Perceptrons
现在我们来看下 Perceptrons 的 VC 维,
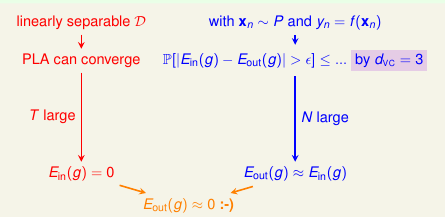
图 7-2
看图 7-2 的红色部分,这是我们在前面的章节中已经得到的结论,即 T 足够的大就能在 in-sample 上得到 E(g) = 0。同时,不管是任何的 hypothesis, 只要 N 足够大就能得出 Ein ≈ Eout 。 这就能得出结论 Eout(g) ≈ 0

图 7-3
从图 7-3 可以看出 1 维的 Perceptron 的 dvc 是维 Perceptron 的 dvc是 3。
我们猜想 d 维 Perceptron 的 dvc = d+1 ?
Prove1:dvc ≥ d + 1。 如图 7-4 所示, 矩阵 X 是可逆矩阵。这组 inputs 能被 hypothesis shatter 掉,因为对于任意 y 都能找到 w = x-1y。即 dvc ≥ d+1
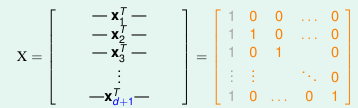
图 7-4
Prove2:dvc ≤ d + 1 。 如图 7-5 所示, 矩阵 X 的 rank 是 d+1, 所以肯定有一行 KK 是其它行的线性组合。所以行 KK 依赖其它行。d 维感知器 hypothesis 不能 shatter d+2 行数据,即 dvc < d+2 也就是 dvc ≤ d+1

图 7-6
我们已经证明对 d 维感知器有 dvc = d + 1
7.3 Physical Intuition of VC Dimension

图 7-7
从图 7-7 看出对 Positive Rays 有一个自由参数,VC Dimension 也是 1。Positive Intervals 有 2 个自由参数, VC Dimension 也是 2。
VC Dimension 的物理意义是 hypothesis 的自由度,有多少可以调的参数。VC Dimesion 越大的 hypothesis 表现能力越强,因为有更多可调参数,同时模型也就越复杂。一般情况下 VC Dimension 都等于自由参数(大体上正确)。
图 7-8

图 7-9
图 7-9 中的讨论,我们在第 5 节课笔记做过类似的讨论。不过那个时候用的 M 没有用到 dvc。对于两个不同 infinite hypothesis, 它们的 VC Dimension 是不同的。还用 M 来讨论就显得很粗糙。在下面第 4 节会细谈有关 VC Dimension 对 Ein 和 Eout 的影响
7.4 Interpreting of VC Dimension
先看 2 个图
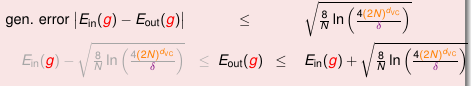
图 7-10

图 7-11
VC Dimension 越大,Ein 会越来越小但是 Eout 和 Ein 的差值也可能越来越大。 通过 VC Dimension 来解释过拟合。
在后续的章节会讨论过拟合和 N、Nosie (随机噪声和确定噪声--希望没说错)、hypothesis VC Dimension 有关。那些讨论得出一些很有趣的结论。
先贴图为敬,这里就不赘述了。

图 7-12 (第14 节课的截图)

图 7-13 (第 13 节课的截图)
图 7-12 和 7-13 是不是很有意思啊!
题外话:
VC Dimension VS 过拟合, VC Dimension 是由数学推导出来的, 过拟合是由结果好坏来判定的。 VC Dimension 和过拟合这两个放在一起就是所谓的 形而上和形而下。