初入数状数组（poj2299）

                                                                                            树状数组

 主要用处：树状数组主要用于涉及带点修改或则区间查询的题目，主要

可以减少时间复杂度。

树状数组实际上是一种涉及二进制的储存方式。

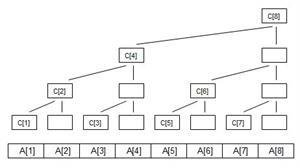
通过树状数组来储存数据可以使在查询和修改的过程中更加的方便。

数状数组的查询：

int getsum(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
ans+=tree[i];
return ans;
}

树状数组的修改：

void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=y;
}

lowbit函数：

int lowbit(int t)
{
return t&(-t);
}

以上代码即可实现单点查询和区间修改

——————————————————————————分隔符——————————————————————————————————————————————————————————————————————

POJ2299：

题目传送门

通过读题我们可以了解到这个题目是求数组的逆序对，因为有以下定理：一个乱序序列的 逆序数 = 在只允许相邻两个元素交换的条件下,得到有序序列的交换次数

那么怎么求逆序对呢？可以通过树状数组来实现。

算法的大体流程：

1.先对数组进性离散化使得各个数据离得比较进

2.运用树状数组的标准操作来来的到逆序对。

那么为什么要进行数据离散化呢，因为我们在储存的过程中，如果有一个很大的数，就需要更多的位空间来进行储存，所以需要对初始数据进性离散化。

先将数组插入数状数组中，然后对其进行修改：

#include<iostream>
#include<algorithm>
typedef long long ll;
#include<cstring>
using namespace std;
#define maxn 510000
int c[maxn],n,a[maxn];
struct node
{
    int val,pos;
}p[maxn];
bool cmp(node a,node b)
{
    return a.val<b.val;
}
void add(int i){
  while(i<=n){
    c[i]+=1;
    i+=i&-i;
  }
}
int sum(int i)
{
    int s=0;
    while(i)
    {
        s+=c[i];
        i-=i&(-i);
    }
    return s;
}

int main()
{
    while(cin>>n)
    {
        if(n==0) break;
        for(int i=1;i<=n;i++)
        {
            int v;
            cin>>v;
            p[i].val=v;
            p[i].pos=i;
        }
        memset(c,0,sizeof(c));
        sort(p+1,p+1+n,cmp);
        for(int i=1;i<=n;i++) a[p[i].pos]=i;
        ll ans=0;
        for(int i=1;i<=n;i++)
        {
            add(a[i]);
            ans+=i-sum(a[i]);
        }
        cout<<ans<<endl;
    }
    return 0;
} 

如果不懂可以看这篇博客：https://blog.csdn.net/guhaiteng/article/details/52138756

专题训练地址：https://vjudge.net/contest/295361