01背包

01背包：指的是每种物品只能选0次或1次的背包问题。

在01背包的基础上说一下闫氏dp分析法：

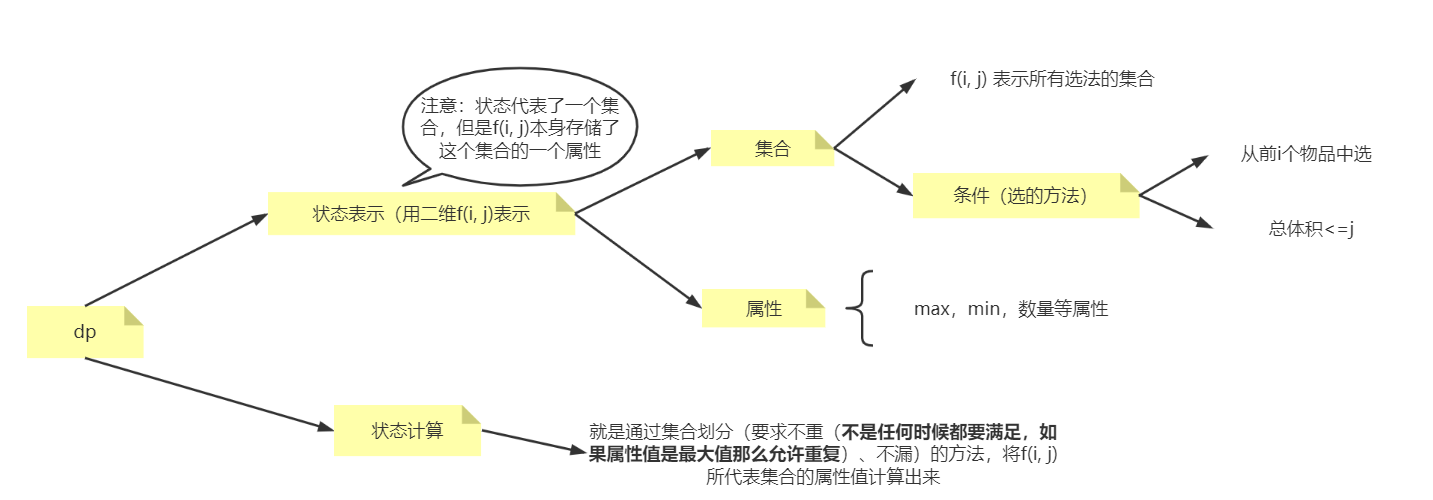
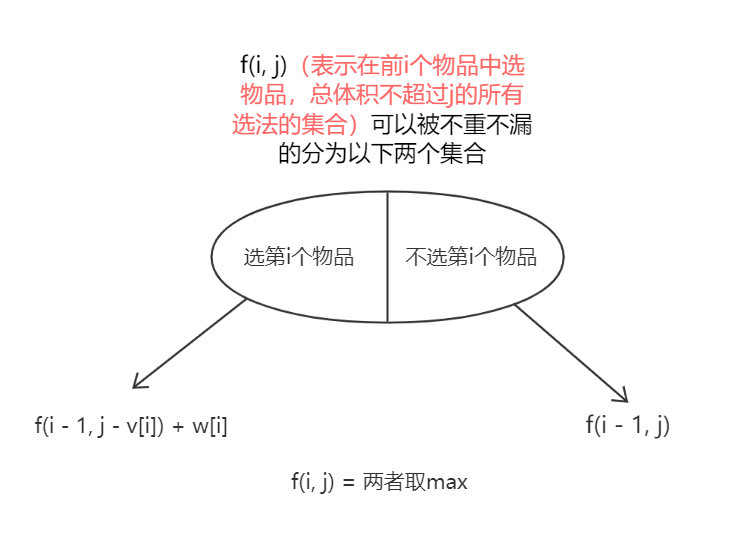
状态计算使用的集合划分方法：

#include<iostream>
using namespace std;

const int N = 1010;

int n, m;
int f[N][N];
int w[N], v[N];

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    //f[0][1 ~ m] = 0
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++){
            //对照图2看一下
            f[i][j] = f[i - 1][j]; // 左侧集合必存在
            if(j - v[i] >= 0) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); // 此处判断是因为如果右侧集合为空就不要再求max了
        }
        
    cout << f[n][m] << endl;
    
    return 0;
}

将空间从二维优化为1维，用代码等价变形的方法。
（不要从代码推思路，要根据思路写代码。--yxc）

#include<iostream>
using namespace std;

const int N = 1010;

int n, m;
int f[N];
int w[N], v[N];

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= v[i]; j --)//注意此处需要倒着来的原因：如果不倒着来==> f[j - v[i]]先被计算，就不是第i - 1层的f[j - v[i]]了，而是第i层的f[j - v[i]]
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        
    cout << f[m] << endl;
    
    return 0;
}

综上dp的分析方法就是：确定状态是什么元素的集合，状态需要用几维表示，状态存了集合的什么属性，一个状态表示的集合应当怎么划分（从而计算出当前状态的属性值），题目的答案是哪一个状态。