完全背包:每一种物品可以选任意多次的背包问题。
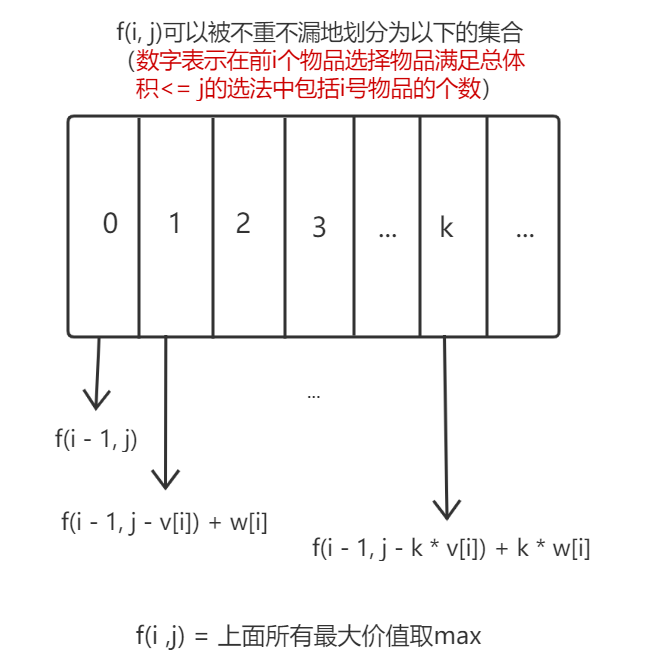
经过分析,可以在01背包的代码基础上,增加一层循环,有以下暴力代码(O(n^3))
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int w[N], v[N];
int f[N][N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
//f[0][1 ~ m] = 0;
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= m; j ++){
f[i][j] = f[i - 1][j];
int k = j / v[i];
for(int t = 1; t <= k; t ++)
f[i][j] = max(f[i][j], f[i - 1][j - t * v[i]] + t * w[i]);
}
}
cout << f[n][m];
return 0;
}
时间上需要优化:
由上图:
(f(i, j) = max(f(i - 1, j), f(i - 1, j - v[i]), f(i - 1, j - 2 * v[i]), ... , f(i - 1, j - k * v[i]), ...))
做一个变量代换,将上式中的j换成(j - v[i])
得(f(i, j - v[i]) = max(f(i - 1, j - v[i]), f(i - 1, j - 2 * v[i]) ,...))
发现第一个式子中(max(f(i - 1, j), 后面一坨))中 (后面一坨 = max(f(i - 1, j), f(i - 1, j - v[i]), ...) = max(f(i - 1, j - v[i]), f(i - 1, j - 2 * v[i]), ...) + w[i] = f(i, j - v[i]) + w[i])
所以得到(f(i, j) = max(f(i - 1, j), f(i, j - v[i]) + w[i]))
所以就可以把上面得第三重循环优化成O(1)的了
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int w[N], v[N];
int f[N][N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
//f[0][1 ~ m] = 0;
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= m; j ++){
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
cout << f[n][m];
return 0;
}
最后通过代码等价变形的方法,把空间优化成1维
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int w[N], v[N];
int f[N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = v[i]; j <= m; j ++)
f[j] = max(f[j], f[j - v[i]] + w[i]); // 此处正好需要的是第i层的f[j - v[i]],所以第二重循环不需要倒着来
cout << f[m];
return 0;
}