题意:给你一个有向图(包括环,自环啥的),你现在在顶点1,要走到顶点n,并且到达每一个顶点的时候,都会获得一个能量值w(可正可负),问你能不能在活着的情况下到达n(就是在到达n的路上不会出现能量<=0,并且到达n的时候能量必须为正)
注意:顶点a的能量值w,其实可以看做是任意一个与a邻接的顶点到达a的边上的权值(下面的图),又因为本题判断存不存在能活着到达n的路径,所以就变成了求从1到n的最长路径

思路:floyd求可达性 + spfa求最长路(中间还要判断正环)
有几种情况:如果1和n不可达,直接hopeless,如果可达,那么有下面几种情况
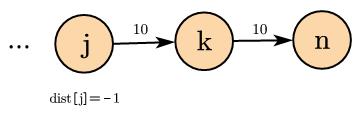
图中不存在正环,spfa可以正常求最长路,但是在求最长路的过程中,如果一个点更新后的最长距离<0, 那么不能把这个点入队(下面的图),如果把点j入队并让他更新后面到n的距离,那么dist[n]=19 > 0, 这样就会错误输出winnable了
图中存在正环,有正环的话,需要判断正环上的点能不能到n,如果可以到n,就直接输出winnable,如果不可以,由于spfa用的是bellman-ford,并且这个负环不会影响1到n的最长路,所以在发现正环的时候,如果1可以到n,那么1到n的最长路已经求出来了,这个时候判断dist[n] 是否大于0就行了
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
const int N = 110;
#define PII pair<int, int>
#define v first
#define w second
PII g[N][N];
bool d[N][N];
int dist[N], st[N], cnt[N];
int n;
int spfa(){
memset(dist, 128, sizeof dist);
memset(st, 0, sizeof st);
memset(cnt, 0, sizeof cnt);
queue<int> q;
st[1] = 1;
dist[1] = 100;
q.push(1);
int res = 0;
while(q.size()){
int a = q.front();
q.pop();
st[a] = 0;
for(int i = 1; i <= n; i ++){
if(g[a][i].v == 0) continue;
if(dist[i] < dist[a] + g[a][i].w){
dist[i] = dist[a] + g[a][i].w;
cnt[i] = cnt[a] + 1;
if(cnt[i] >= n){
if(d[i][n]) return 1;
return dist[n] > 0;
}
if(st[i] == 0 && dist[i] > 0){
st[i] = 1;
q.push(i);
}
}
}
}
return dist[n] > 0;
}
int main(){
while(cin >> n, ~n){
memset(d, 0, sizeof d);
memset(g, 0, sizeof g);
for(int i = 1; i <= n; i ++){
int p, c;
cin >> p >> c;
for(int j = 0; j < c; j ++){
int b;
cin >> b;
g[i][b].v = 1;
d[i][b] = 1;
}
for(int j = 1; j <= n; j ++)
g[j][i].w = p;
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
for(int k = 1; k <= n; k ++)
d[i][j] = d[i][j] || (d[i][k] && d[k][j]);
if(!d[1][n]){
cout << "hopeless" << endl;
continue;
}
if(spfa()) cout << "winnable" << endl;
else cout << "hopeless" << endl;
}
return 0;
}