简单插入排序
适用于记录较少且基本有序的记录。算法思想:给定一个存在分界线的序列,分界线左边有序,右边无序,依次将右边的没排序的数与左边序列进行比较,插入相应位置,再对分界线做出相应调整,下面用图来说明。
代码如下:
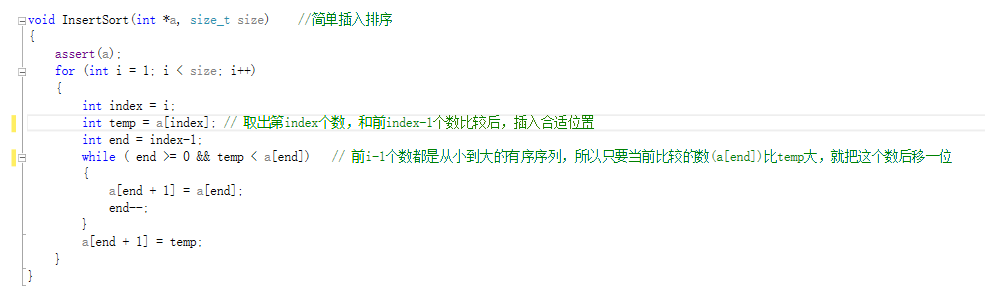
时间复杂度:最好情况O(n),最坏O(n^2)。
希尔排序
希尔排序是改进后的简单插入排序。算法思想:将序列分组排序,最后在进行一次简单插入排序。
至于如何分组,下面我将用图向大家展示

这些数的下标从0开始,即0,3 ,6,9为一组,1,4,7为一组,2,5,8为一组。也就是gap%3下标相等的为一组。gap=gap/3+1.
代码如下:
void ShellSort(int *a, size_t size) //希尔排序
{
assert(a);
int gap = size;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = gap; i < size; ++i)
{
int index = i;
int tem = a[index];
int end = index - gap;
while (end >= 0 && tem < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = tem;
}
}
}
时间复杂度为O(n^1.5)
选择排序
算法思想:每次循环找到最小值,并交换。

代码如下:
void SelectSort(int *a, size_t size)
{
assert(a);
for (int i = 0; i < size; ++i)
{
int minindex = i;
int tem;
for (int j = i + 1; j < size; ++j)
{
if (a[j] < a[minindex])
{
minindex = j;
tem = a[minindex];
a[minindex] = a[i];
a[i] = tem;
}
}
}
}
时间复杂度O(n^2)
快速排序
算法思想:选取key,将key调整到一个合理的位置,使得左边全部小于key,右边全部大于key;
如何将key调整到合适位置,这里用到三数取中的方法。
注意:如果序列基本有序或序列个数较少,则可以采用简单插入排序,因为快速排序对于这些情况效率不高;
代码如下:
int GetMidIndex(int *a, int left, int right) /////////三数取中/////////
{
assert(a);
int mid=left+(right-left)/2;
if (left < right)
{
if (a[mid] < a[left])
return left;
else if (a[mid] < a[right])
return mid;
else
return right;
}
else
{
if (a[mid] < a[right])
return right;
else if (a[mid] < a[left])
return mid;
else
return left;
}
}
int PartionSort(int *a, int left, int right)
{
int midIndex = GetMidIndex(a, left, right);
swap(a[midIndex], a[right]);
int cur = left;
int prev = left - 1;
while (cur < right)
{
if (a[cur] < a[right] && ++prev != cur)
{
swap(a[cur], a[prev]);
}
++cur;
}
++prev;
swap(a[prev], a[right]);
return prev;
}
void QuickSort(int *a,int left,int right)
{
assert(a);
int size = right - left + 1;
if (right - left > 13) //////////优化:当长度大于13时采用快排,小于13则退化为简单插入排序////////////
{
int boundary = PartionSort(a, left, right);
QuickSort(a, left, boundary - 1);
QuickSort(a, boundary + 1, right);
}
else
InsertSort(a, size); /////简单插入排序
}
冒泡排序
算法思想:两两比较再交换,一趟排序下来只能找到一个最大,其余都是乱序,再重复这样做就可以按照从小到大的顺序排下来。
代码如下:
void BubbleSort(int *a, size_t size)
{
assert(a);
for (int i = 0; i < size; i++)
{
for (int j = 0; j = size - 1 - i; j++)
{
if (a[j] > a[j + 1])
{
int tem = a[j + 1];
a[j + 1] = a[j];
a[j] = tem;
}
}
}
}
以上冒泡排序有一个效率问题,当序列基本接近有序时,则不需要进行排序,以上代码则会进行不断的比较,影响效率,因此做以下改进,设一个布尔型变量flag,
如果一次循环中没有交换过元素,则说明已经排好序.
优化:
void BubbleSort(int *a, size_t size)
{
assert(a);
bool flag=true;
for (int i = 0; i < size; i++)
{
bool flag=false;
for (int j = 0; j = size - 1 - i; j++)
{
if (a[j] > a[j + 1])
{
int tem = a[j + 1];
a[j + 1] = a[j];
a[j] = tem;
bool flag=true;
}
}
}
}
堆排序
算法思想:将待排序列建成大堆,再将堆顶数据与堆的最后一个叶子节点的数据交换,再重新调整为大堆,每次堆的数据个数减1。

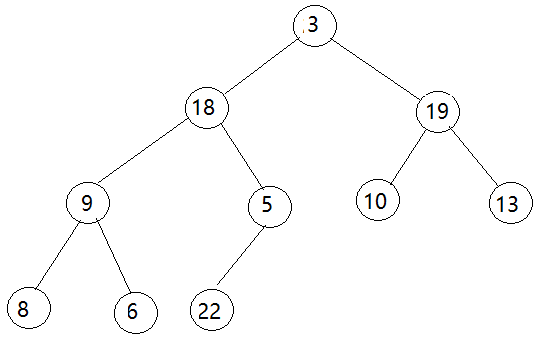
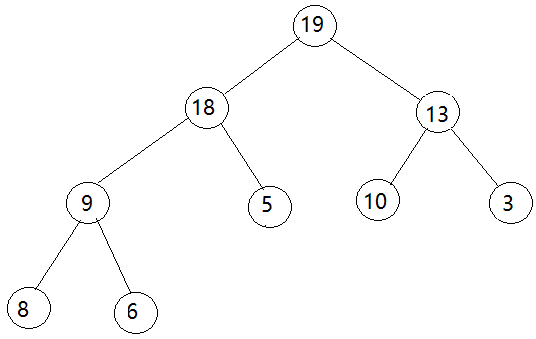

依次类推......
代码如下:
void HeapSort(int *a, size_t size) //堆排序
{
assert(a);
for (int i = (size - 2) / 2; i >= 0; --i)
{
Adjustdown(a, size, i);
}
for (int i = 0; i < size; ++i)
{
swap(a[0], a[size - i - 1]);
Adjustdown(a, size - i - 1, 0);
}
}
/////////建大堆/////////
void Adjustdown(int *a, size_t size, int root)
{
int child = 2 * root + 1;
while (child < size)
{
if (child + 1 < size && a[child + 1] > a[child])
{
++child;
}
if (a[child]>a[root])
{
swap(a[child], a[root]);
root = child;
child = 2 * root + 1;
}
else
{
break;
}
}
}