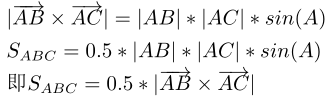经典问题一：求n个点围成的多边形的面积
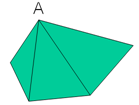
对于凸多边形，很容易计算，如下图，以多边形的某一点为顶点，将其划分成几个三角形，计算这些三角形的面积，然后加起来即可。已知三角形顶点坐标，三角形面积可以利用向量的叉乘来计算。
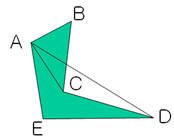
对于凹多边形，如果还是按照上述方法划分成三角形，如下图，多边形的面积 = S_ABC + S_ACD + S_ADE, 这个面积明显超过多边形的面积。
我们根据二维向量叉乘求三角形ABC面积时，利用的是
这样求出来的面积都是正数，但是向量叉乘是有方向的，即
是有正负的，如果把上面第三个公式中的绝对值符号去掉，即
，那么面积也是有正负的。反应在上面第二个图中，S = S_ABC + S_ACD + S_ADE，如果S_ABC和S_ADE是正的，那么S_ACD是负的，这样加起来刚好就是多边形的面积。对于凸多边形，所有三角形的面积都是同正或者同负。
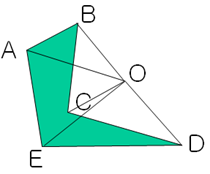
如果我们不以多边形的某一点为顶点来划分三角形而是以任意一点，如下图，这个方法也是成立的：S = S_OAB + S_OBC + S_OCD + S_ODE + S_OEA。计算的时候，当我们取O点为原点时，可以简化计算。 本文地址
当O点为原点时，根据向量的叉积计算公式，各个三角形的面积计算如下：
S_OAB = 0.5*(A_x*B_y - A_y*B_x) 【(A_x，A_y)为A点的坐标】
S_OBC = 0.5*(B_x*C_y - B_y*C_x)
S_OCD = 0.5*(C_x*D_y - C_y*D_x)
S_ODE = 0.5*(D_x*E_y - D_y*E_x)
S_OEA = 0.5*(E_x*A_y - E_y*A_x)
代码如下
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
struct Point2d{ double x; double y; Point2d(double xx, double yy): x(xx), y(yy){}};//计算任意多边形的面积，顶点按照顺时针或者逆时针方向排列double ComputePolygonArea(const vector<Point2d> &points){ int point_num = points.size(); if(point_num < 3)return 0.0; double s = 0; for(int i = 0; i < point_num; ++i) s += points[i].x * points[(i+1)%point_num].y - points[i].y * points[(i+1)%point_num].x; return fabs(s/2.0);} |
该算法还可以优化一下，对上面的式子合并一下同类项
S = S_OAB + S_OBC + S_OCD + S_ODE + S_OEA =
0.5*(A_y*(E_x-B_x) + B_y*(A_x-C_x) + C_y*(B_x-D_x) + D_y*(C_x-E_x) + E_y*(D_x-A_x))
这样减少了乘法的次数，代码如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
struct Point2d{ double x; double y; Point2d(double xx, double yy): x(xx), y(yy){}};//计算任意多边形的面积，顶点按照顺时针或者逆时针方向排列double ComputePolygonArea(const vector<Point2d> &points){ int point_num = points.size(); if(point_num < 3)return 0.0; double s = points[0].y * (points[point_num-1].x - points[1].x); for(int i = 1; i < point_num; ++i) s += points[i].y * (points[i-1].x - points[(i+1)%point_num].x); return fabs(s/2.0);} |
【版权声明】转载请注明出处：http://www.cnblogs.com/TenosDoIt/p/4047211.html
经典问题：判断多边形的凹凸性
描述
任意给定一个多边形，判断它是凸还是凹。多边形的顶点以逆时针方向的序列来表示。
输入
输入包含多组测试数据，每组数据占2行，首先一行是一个整数n，表示多边形顶点的个数，然后一行是2×n个整数，表示逆时针顺序的n个顶点的坐标（xi,yi），n为0的时候结束输入。
输出
对于每个测试实例，如果地块的形状为凸多边形，请输出“convex”,否则输出”concave”，每个实例的输出占一行。
样例输入
4 0 0 1 0 1 1 0 1 0
样例输出
convex
代码：
分析：
按照输入顺序依次将点连接起来
对于连续的三个点p0,p1,p2，另向量a=p1-p0，b=p2-p1
若是凸多边形，那么b相对于a一定是向逆时针方向旋转的
判断两向量的旋转方向，可以使用向量的叉积 a×b ＝ x1×y2 － x2×y1
a×b > 0 b在a的逆时针方向
a×b = 0 b平行于a（共线）
a×b < 0 b在a的顺时针方向
要注意的是，对于最后一个点pn，还要和起始的两个点p0,p1判断一次。
===================================================
#include <stdio.h> typedef struct{ int x,y; }Point; int det(int x1,int y1,int x2,int y2){ return x1*y2 - x2*y1; } int corss(Point p0,Point p1,Point p2){ return det(p1.x-p0.x,p1.y-p0.y, p2.x-p1.x,p2.y-p1.y); } void getP(Point *p){ scanf("%d%d",&(p->x),&(p->y)); } int main() { int i,j,k,m,n; int s,flag; Point p0,q0,p,q,r; while(scanf("%d",&n),n){ if(n<3){ for(i=0;i<n;i++) scanf("%*d%*d"); puts("convex"); continue; } flag=1; getP(&p0); getP(&q0); r=p0; p=q0; for(i=2;i<n;i++){ getP(&q); if(corss(r,p,q)<0) flag=0; r=p; p=q; } if(corss(r,p,p0)<0) flag=0; if(corss(p,p0,q0)<0) flag=0; if(flag) puts("convex"); else puts("concave"); } return 0; }
注意，这个要求人工按顺序输入点。。。