Problem Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
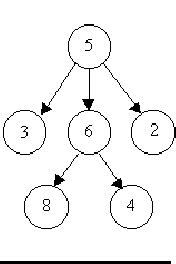
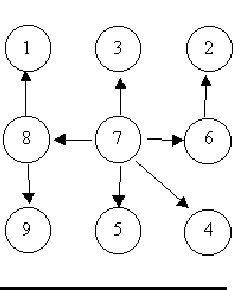
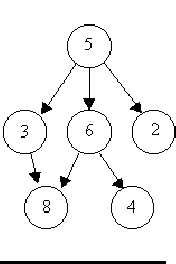
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input** will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line Case k is a tree." or the lineCase k is not a tree.”, where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
思路
- 首先我们通过并查集来记录数据,然后判断是否存在环
- 题目中的输入数据为有向边,然后我们判断是否为树的条件是是否有且只有一个度为0的节点,此节点即为根节点。
code
//accepted
//Exe.Time Exe.Memory
// 15MS 1696K
#include <iostream>
#include <fstream>
#include <cstring>
const int MAX = 10000 + 5;
int father[MAX];
bool vis[MAX];
int e[MAX]; //记录节点的入度
void init()
{
for(int i = 0; i < MAX; ++ i)
{
father[i] = i;
}
}
//寻找并查集的根节点,并按路径压缩
int find(int x)
{
if(x != father[x])
{
father[x] = find(father[x]);
}
return father[x];
}
//合并两个并查集
void meger(int x, int y)
{
int x0 = find(x);
int y0 = find(y);
father[y0] = x0;
}
using namespace std;
int main()
{
//ifstream cin("data.in");
int x, y;
int cnt = 1;
while(cin >> x >> y && x >= 0 && y >= 0)
{
memset(e, 0, sizeof(e));
memset(vis, false, sizeof(vis));
init();
bool ok = true;
while(x != 0 || y != 0)
{
int x0 = find(x);
int y0 = find(y);
vis[x] = vis[y] = true;
if(x0 == y0)//当出现另个节点的集合的根一样时,即存在环
{
ok = false;
}
meger(x0, y0);
e[y] ++;
cin >> x >> y;
}
int m = 0;
for(int i = 0; i < MAX; ++ i)
{
//判断入度为0的节点,即根节点
if(vis[i] && e[i] == 0)
{
m ++;
}
}
if(ok && (m == 1 || m == 0))
{
cout << "Case " << cnt ++ << " is a tree." << endl;
}
else
{
cout << "Case " << cnt ++ << " is not a tree." << endl;
}
}
return 0;
}