你以为这是道博弈论题目,其实……的确是啊
把考场上的思路完整的说一下
首先考虑倒推,如果最后一格的数是奇数,会怎么样?
以样例为例
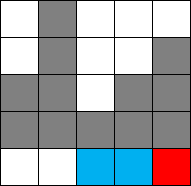
显然,如果我们走到了最后一格,就只能在上面反复横跳,直到这一列的格子完全消失
很容易发现,这样的情况,最后一列就是一个必胜点(这里必胜点定义为先走到这里一定获胜)
那么,在这一列的前面m列之内,所有列都是必败点(因为如果走到这里,下一步对手一定可以走到必胜点)
用红色表示必胜点,蓝色表示必败点

接着继续考虑,如果要尽量避免走到蓝色的列(必败点),最后两人一定会在第二列上反复横跳,直到这一列消失
是不是很熟悉?对!这是和最开始情况一样的!
但这里,最后一格是偶数,显然它是必败点(先手过去一定会输)
那它前面那一列是什么点呢?因为是偶数,所以继承了前面的情况,也是必败点
到这里,我们已经可以得出一个结论了:
倒推,如果最后一列是奇数,那么这一列是必胜点,它前面的m列都必败
如果最后一列是偶数,那么这一列是必败点,所有玩家都会尽量避免走到这一列来
所以我们可以考虑连边!顺序枚举,对于每一列,把它前面的第一个必胜点向他连边
这样的话,连好后的图是一个以0为根的多叉树形结构!
对于每次的询问l和r,如果l是r的祖先,那么先手必胜,否则后手必胜!
那么现在的问题来了,给出一棵固定形态的树,怎么(Theta(1))地判断u是否是v的祖先呢?
dfs序!
在dfs的过程中统计一个点第一次被访问到的时间戳,作为其dfn
如果(dfn[u]leq dfn[v] leq dfn[u]+size[u]-1)的话,u就是v的祖先!
那么这题就这样解决啦!
具体的看代码吧
#include<bits/stdc++.h>
#define mod (1LL<<32)
#define ll long long
#define int long long
#define N 20000005
using namespace std;
int n,m,q,type,l[N],r[N];
int L,a[N],fa[N];//fa->这个点前面的第一个必胜转移点
ll ans=0;
int A,B,C,P;
inline int rnd(){return A=(A*B+C)%P;}
struct Edge
{
int next,to;
}edge[N];
int cnt=0,head[N];
inline void add_edge(int from,int to)
{
edge[++cnt].next=head[from];
edge[cnt].to=to;
head[from]=cnt;
}
template<class T>inline void read(T &res)
{
char c;T flag=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
}
int siz[N],dfn[N],tms;
void dfs(int u,int fa)
{
// cout<<"dfs: "<<u<<" "<<fa<<endl;
siz[u]=1;
if(!dfn[u]) dfn[u]=++tms;
for(register int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
dfs(v,u);
siz[u]+=siz[v];
}
}
signed main()
{
read(n);read(m);read(q);read(type);//数的个数,区间长度,询问,是否压缩
for(register int i=1;i<=n;++i) read(a[i]);
if(!type)
{
for(register int i=1;i<=q;++i)
read(l[i]),read(r[i]);
}
else
{
read(A);read(B);read(C);read(P);
for(register int i=1;i<=q;++i)
{
l[i]=rnd()%n+1;
r[i]=rnd()%n+1;
if(l[i]>r[i]) swap(l[i],r[i]);
}
}
for(register int i=1;i<=n;++i)
{
L=max(0LL,i-m-1);
if(a[i]&1)//奇数是必胜点
{
if(a[L]&1) fa[i]=L,add_edge(L,i);
else fa[i]=fa[L],add_edge(fa[L],i);
}
else//偶数,先手必败
{
if(a[i-1]&1) fa[i]=i-1,add_edge(i-1,i);
else fa[i]=fa[i-1],add_edge(fa[i-1],i);
}
}
//处理出每个点倒序第一个必胜转移点
dfs(0,0);//dfs序
// for(register int i=1;i<=n;++i) cout<<siz[i]<<endl;
for(register int i=1;i<=q;++i)
{
int u=l[i],v=r[i];
if(u==v)
{
if(a[u]&1) continue;
else ans=(ans+i*i)%mod;
continue;
}
// cout<<dfn[u]<<" "<<dfn[v]<<" "<<dfn[u]+siz[u]-1<<endl;
if(dfn[u]<=dfn[v]&&dfn[v]<=dfn[u]+siz[u]-1) continue;//先手必胜,没有贡献
ans=(ans+i*i)%mod;
}
printf("%lld
",ans);
return 0;
}
/*
4 2 1 0
2 2 0 0
1 4
*/