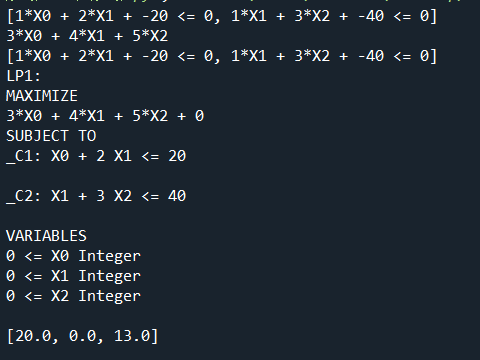
解如下整数线性规划
maximize z = cx = 3x1 + 4x2 + 5x3
subject to :
x1 2 3 >= 0
x1 + 2x2 < 20
x2 + 3x3 <= 40
import pulp as pulp
def solve_ilp(objective , constraints) :
print(objective)
print(constraints)
prob = pulp.LpProblem('LP1' , pulp.LpMaximize)
prob += objective
for cons in constraints :
prob += cons
print(prob)
status = prob.solve()
if status != 1 :
return None
else :
return [v.varValue.real for v in prob.variables()]
V_NUM = 3
#变量,直接设置下限,约束条件中的不等式只支持>=或<=,不支持<和>
#如果是解线性规划只需要在生成变量时cat = pulp.LpContinuous
variables = [pulp.LpVariable('X%d'%i , lowBound = 0 , cat = pulp.LpInteger) for i in range(0 , V_NUM)]
#目标函数
c = [3 , 4 , 5]
objective = sum([c[i]*variables[i] for i in range(0 , V_NUM)])
#约束条件
constraints = []
a1 = [1 , 2 , 0]
constraints.append(sum([a1[i]*variables[i] for i in range(0 , V_NUM)]) <= 20)
a2 = [0 , 1 , 3]
constraints.append(sum([a2[i]*variables[i] for i in range(0 , V_NUM)]) <= 40)
print(constraints)
res = solve_ilp(objective , constraints)
print(res)
运行结果: