约瑟夫环的三种解法

什么是约瑟夫环问题

• 已知 n 个人（以编号1，2，3 … n 分别表示）围成一圈。从编号为 1 的人开始报数，数到 m 的那个人出列；他的下一个人又从 1 开始报数，数到 m 的那个人又出列；依此规律重复下去，直到最后剩下一个人。要求找出最后出列的人的编号

  可能有些同学看到的不是从编号为 1 的人开始报数，但我想说，不管从编号为几的人开始报数，其实都可以将这个第一个开始报数的人的编号看作是 1，在得出最后出列的人的编号之后，我们很容易就可以将其转为从编号为 1 的人开始报数的情况下，最后一个出列的人的编号

用数组解决

• 用数组来解决，应该是很多第一次接触到这个问题的人最容易想到的一种方式，思想很简单，但实现起来需要考虑的地方还是很多的

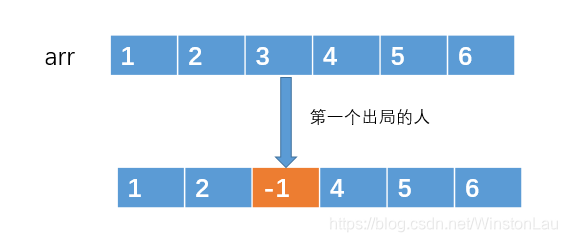
1. 用一个数组来存放 1，2，3 … n 这 n 个编号（假设 n = 6, m = 3，k = 1）
   

2. 然后不停着遍历数组，对于被选中的编号，我们就做一个标记，例如编号 arr[2] = 3 被选中了，那么我们可以做一个标记，例如让 arr[2] = -1，来表示 arr[2] 存放的编号已经出局了
   

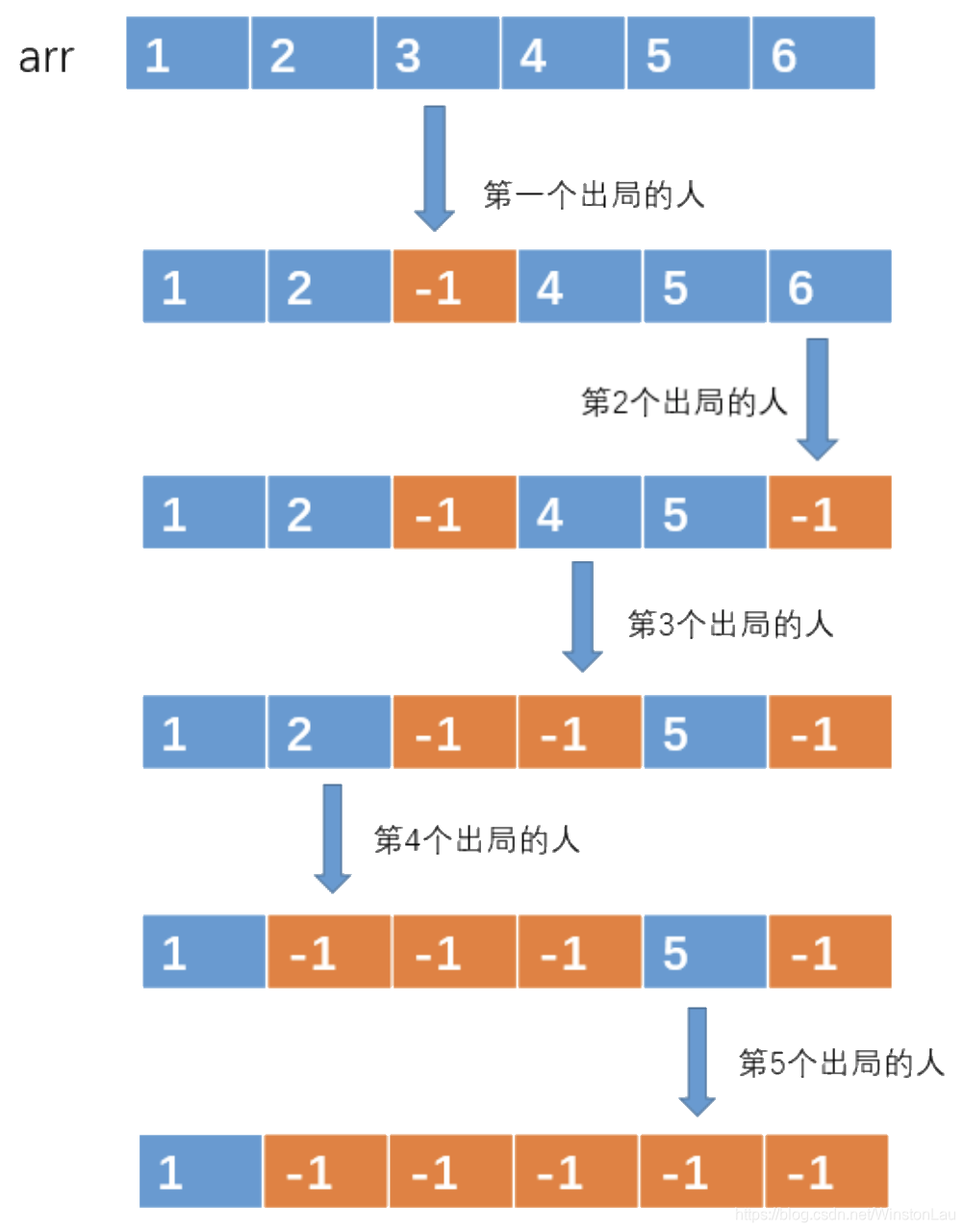
3. 然后就按照这种方法，不停着遍历数组，不停着做标记，直到数组中只有一个元素是非 -1 的，这样，剩下的那个元素就是我们要找的元素了。演示如下
   

4. 编码实现这里就不写了，本文的重点在第三种方法

5. 这种做法的时间复杂度是 O(nm), 空间复杂度是 O(n)

用环形链表解决

• 用链表来处理其实和上面处理的思路差不多，只是用链表来处理的时候，对于被选中的编号，不再是做标记，而是直接移除，因为从链表移除一个元素的时间复杂度很低，为 O(1)

• 当然，上面数组的方法你也可以采用移除的方式，不过数组移除的时间复杂度为 O(n)

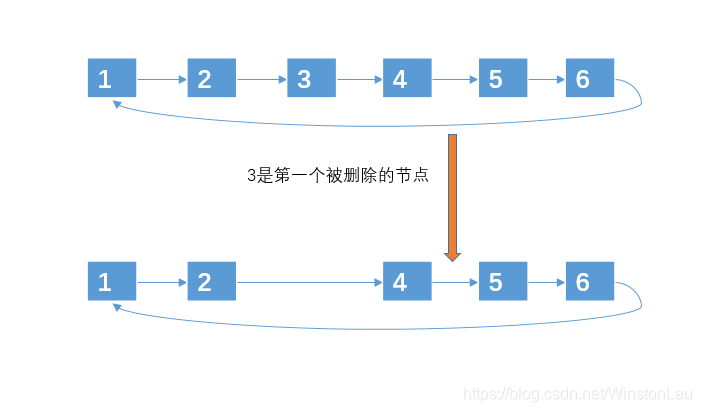
1. 先创建一个环形链表来存放元素
   

2. 然后在遍历链表的同时做删除操作，这里就不全部演示了
   

3. 核心代码如下：

   // 定义链表节点
   class Node{
       int date;
       Node next;
   
       public Node(int date) {
           this.date = date;
       }
   }
   
   
    public static int solve(int n, int m) {
           if(m == 1 || n < 2)
               return n;
           // 创建环形链表
           Node head = createLinkedList(n);
           // 遍历删除
           int count = 1;
           Node cur = head;
           Node pre = null;//前驱节点
           while (head.next != head) {
               // 删除节点
               if (count == m) {
                   count = 1;
                   pre.next = cur.next;
                   cur = pre.next;
               } else {
                   count++;
                   pre = cur;
                   cur = cur.next;
               }
           }
           return head.date;
       }
   
       static Node createLinkedList(int n) {
           Node head = new Node(1);
           Node next = head;
           for (int i = 2; i <= n; i++) {
               Node tmp = new Node(i);
               next.next = tmp;
               next = next.next;
           }
           // 头尾串联
           next.next = head;
           return head;
       }
   

4. 这种做法的时间复杂度是 O(nm), 空间复杂度是 O(n)，和第一种方法一样

用递归解决

• 为了解决上面两种方法的效率问题，我们可以从数学角度对这个问题进行分析，找出其中的规律，然后使用递归实现

• 为了方便导出递归公式，这里先对问题做个简短的定义

• 问题定义：有 n 个人，编号为 1，2，……，n，从编号为 1 的人开始，从 1 开始依次报数，每报到 m 时，该人出列，求最后出列的人的编号

• 我们首先定义一个函数 f(n,m)f(n,m) f(n,m)$f(n,m)$f(n,m)，它表示的是 nn n$n$n 个人报数，每报到 mm m$m$m 的人出列，最后出列的人的编号。显然问题的最小规模就是当 n = 1 时，此时 f(1,m)=1f(1,m)=1 f(1,m) = 1$f(1,m) = 1$f(1,m)=1

• f(n−1,m)f(n−1,m) f(n-1,m)$f(n-1,m)$f(n−1,m) 表示的是 n−1n−1 n-1$n-1$n−1 个人报数，每报到 mm m$m$m 的人出列，最后出列的人的编号

• 这里先把结论给出来：f(n,m)=(f(n−1,m)+m)%nf(n,m)=(f(n−1,m)+m)%n f(n,m)=(f(n-1,m)+m) \% n$f(n,m)=(f(n-1,m)+m) \% n$f(n,m)=(f(n−1,m)+m)%n

• 这个公式是如何推导出来的呢？我们已经知道，f(n−1,m)f(n−1,m) f(n-1,m)$f(n-1,m)$f(n−1,m) 表示的是总人数为 n - 1 个时，最后出列的人的编号，假如暂不考虑数组越界的问题，那么当总人数为 n 时，最后出列的人的编号就是 f(n−1,m)+mf(n−1,m)+m f(n-1,m)+m$f(n-1,m)+m$f(n−1,m)+m 。为了防止数组越界，所以我们对 n 取余数

  有些人看到这个解释可能很模糊，其实很简单。我们这样想：反正总共是 n 个人，后一次出列的人的编号肯定是比前一次出列的人的编号大 mm m$m$m 的，同时为了兼顾数组越界的情况，我们需要对 nn n$n$n 取余数

• 下面给出代码实现：

  public int solution(int n, int m) {
          int p = 0;
          // 从第二个人开始遍历所有的人
          for (int i = 2; i <= n; i++) {
              p = (p + m) % i;
          }
          return p + 1; // 最后出列的人的编号
      }
  

• 如果要用递归，就是这样写

  public int f(int n, int m) {
      if(n == 1)   return n;
      return (f(n - 1, m) + m - 1) % n + 1;
  }
  

  • 这里没有写成 return (f(n - 1, m) + m ) % n，主要是因为编号是从 1 开始的，而不是从 0 开始的
  • 另可参考这里

• 如果编号从 0 开始，则最后的返回值表示的是数组的下标，要想得到编号，最终的返回结果还需要加 1，代码如下

  public class YueSheFu {
  
      public static void main(String[] args) {
          int position = f(5,3);
          System.out.println("最后出列的人的编号为：" + (position + 1));
      }
  
      public static int f(int n, int m) {
          if(n == 1) {
              return 0;
          }
          return (f(n - 1, m) + m) % n;
      }
  }
  

https://blog.csdn.net/WinstonLau/article/details/99701837