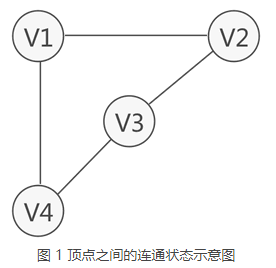
图中从一个顶点到达另一顶点,若存在至少一条路径,则称这两个顶点是连通着的。例如图 1 中,虽然 V1 和 V3 没有直接关联,但从 V1 到 V3 存在两条路径,分别是 V1-V2-V3 和 V1-V4-V3,因此称 V1 和 V3 之间是连通的。
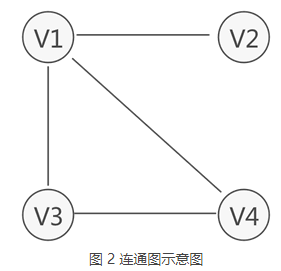
无向图中,如果任意两个顶点之间都能够连通,则称此无向图为连通图。例如,图 2 中的无向图就是一个连通图,因为此图中任意两顶点之间都是连通的。
若无向图不是连通图,但图中存储某个子图符合连通图的性质,则称该子图为连通分量。
前面讲过,由图中部分顶点和边构成的图为该图的一个子图,但这里的子图指的是图中"最大"的连通子图(也称"极大连通子图")。
如图 3 所示,虽然图 3a) 中的无向图不是连通图,但可以将其分解为 3 个"最大子图"(图 3b)),它们都满足连通图的性质,因此都是连通分量。
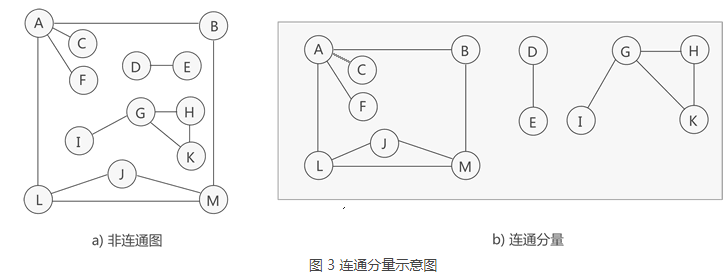
提示,图 3a) 中的无向图只能分解为 3 部分各自连通的"最大子图"。
需要注意的是,连通分量的提出是以"整个无向图不是连通图"为前提的,因为如果无向图是连通图,则其无法分解出多个最大连通子图,因为图中所有的顶点之间都是连通的。
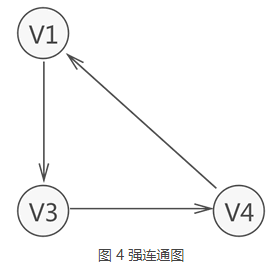
强连通图
有向图中,若任意两个顶点 Vi 和 Vj,满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通,也就是都含有至少一条通路,则称此有向图为强连通图。如图 4 所示就是一个强连通图。
与此同时,若有向图本身不是强连通图,但其包含的最大连通子图具有强连通图的性质,则称该子图为强连通分量。
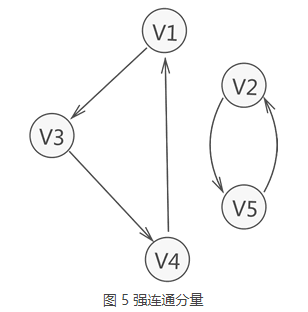
如图 5 所示,整个有向图虽不是强连通图,但其含有两个强连通分量。
可以这样说,连通图是在无向图的基础上对图中顶点之间的连通做了更高的要求,而强连通图是在有向图的基础上对图中顶点的连通做了更高的要求。




