zoukankan html css js c++ java

【Gym-102822C/2020CCPC绵阳C】Code a Trie（大力分类讨论+Trie树/字典树+贪心）

题目链接：http://codeforces.com/gym/102822/problem/C

参考题解：https://blog.csdn.net/qq_39599067/article/details/109579930

题目大意

~~参考题解里面题意已经写的很清楚了，我就不复读了。~~

思路

无解情况为：

两个字符串相同但是权值不同。-> 用(map)维护即可
多个权值对应的 (LCA) 是同一节点。-> 每次标记 (LCA) 时查询一下即可。
(rt)到某个 (lca) 路径上存在 (die) 节点。-> 跑一遍 (dfs) 即可。

假设有 (m) 个字符串权值相同，他们在 (lca) 后的出边是： (a) , (b) , (c) , (d)。
可以肯定的是这四条出边对应节点的子树内不能有其他权值的 (lca) 节点。
我们将 (lca) 这些出边对应的节点标记为不可能存在的节点，即 (die[node]=1)。

注意到多个串如果具有相同的值，那么肯定会在其 (LCA) 处分离。那么对于这些多串，也就应该在 (LCA) 处断裂，对于延伸出来的子树应当不再存在。

举个例子:

3
ab 1
ac 1
ad 2

那么其构成的字典树为：

那么对于节点 (2) 延伸出去的 (b) 边和 (c) 边指向的节点，其不能够再存在子树。

标记后结果如下：

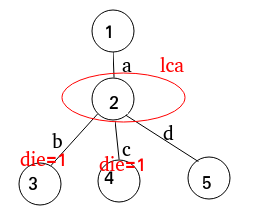
构建完成后，保证有解之后开始统计最少的节点个数。

如果一个节点 (u) 本身不是 (LCA), 其存在子节点的 (lca) 个数为 (1)，那么则将这个子节点翻到节点 (u)，这一过程能够用 (vis) 数组进行维护，来判断当前节点是否有必要存在。

AC代码

#include <bits/stdc++.h>

#define SZ(x) (int)x.size()
using namespace std;
const int MAXN = 1e5 + 5;
const int MAXLOG = 22;
namespace Discrete {
    int b[MAXN], btol, blen;

    void insert(int x) { b[btol++] = x; }

    void init() {
        sort(b, b + btol);
        blen = unique(b, b + btol) - b;
    }

    int val2id(int x) {
        return lower_bound(b, b + blen, x) - b + 1;
    }
}
using Discrete::val2id;


class TRIE {
public:
    int T[MAXN][26], top;

    void init() {
        top = 1;
        memset(T[top], 0, sizeof(T[top]));
    }

    int insert(const string &s, int n) {
        int u = 1;
        for (int i = 0; i < n; i++) {
            int ch = s[i] - 'a';
            if (!T[u][ch]) {
                T[u][ch] = ++top;
                memset(T[top], 0, sizeof(T[top]));
            }
            u = T[u][ch];
        }
        return u;
    }

    int dep[MAXN], fa[MAXN][MAXLOG], lg[MAXN];

    void init(int _n) {
        for (int i = 1; i <= _n; i++) {
            lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
        }
    }


    inline void dfs(int u, int f) {
        fa[u][0] = f, dep[u] = dep[f] + 1;
        for (int i = 1; i <= lg[dep[u]]; i++) fa[u][i] = fa[fa[u][i - 1]][i-1];
        for (int i = 0; i < 26; i++) {
            int v = T[u][i];
            if (v == f) continue;
            if (v) dfs(v, u);
        }
    }

    void get_lca() {
        for (int i = 1; i <= top; i++) memset(fa[i], 0, sizeof(fa[i]));
        dep[1] = 0;
        dfs(1, 1);
    }

    int LCA(int u, int v) {
        if (dep[u] < dep[v]) swap(u, v);
        while (dep[u] > dep[v]) u = fa[u][lg[dep[u] - dep[v]] - 1];
        if (u == v) return u;
        for (int k = lg[dep[u]] - 1; k >= 0; k--) {
            if (fa[u][k] != fa[v][k]) u = fa[u][k], v = fa[v][k];
        }
        return fa[u][0];
    }

    int lca_val[MAXN], die[MAXN];

    void find_lca_init() {
        for (int i = 1; i <= top; i++) lca_val[i] = 0;
        for (int i = 1; i <= top; i++) die[i] = 0;
    }

    int dfs_die(int u, int die_flag) {
        if (die[u]) die_flag = 1;
        if (lca_val[u] && die_flag) return 0;
        for (int i = 0; i < 26; i++) {
            int v = T[u][i];
            if (v) {
                if (!dfs_die(v, die_flag)) return 0;
            }
        }
        return 1;
    }

    int lca_cnt[MAXN], vis[MAXN];

    inline void dfs_ans(int u) {
        int fg = 0;
        for (int i = 0; i < 26; i++) {
            int v = T[u][i];
            if (v) {
                dfs_ans(v);
                lca_cnt[u] += lca_cnt[v];
                if (lca_cnt[v] == 1) {
                    fg = v; //break;
                }
            }
        }
        if (lca_val[u]) lca_cnt[u]++;
        if (!lca_val[u] && fg) {
            vis[u] = 1, vis[fg] = 0;
        } else if (lca_cnt[u]) vis[u] = 1;

    }

    int solve() {
        for (int i = 1; i <= top; i++) lca_cnt[i] = vis[i] = 0;
        dfs_ans(1);
        int ans = 0;
        for (int i = 1; i <= top; i++) ans += vis[i];//, printf("%d
", lca_cnt[i]);
        return ans;
    }

} tree;


string str[MAXN];
int val[MAXN], endpos[MAXN];
vector<int> vec[MAXN];

int main() {
    tree.init(MAXN - 1); // init for lg
    int T;
    cin >> T;
    int kass = 1;
    while (T--) {
        Discrete::btol = 0;
        int n;
        cin >> n;
        for (int i = 1; i <= n; i++) {
            cin >> str[i] >> val[i];
            Discrete::insert(val[i]);
        }
        Discrete::init();
        for (int i = 1; i <= n; i++) val[i] = val2id(val[i]);

        unordered_map<int, int> ma; // same string two val
        int res = 1;

        tree.init();
        for (int i = 1; i <= n; i++) {
            endpos[i] = tree.insert(str[i], SZ(str[i]));
            if (ma.find(endpos[i]) != ma.end()) {
                if (ma[endpos[i]] != val[i]) {
                    res = 0;
                    break;
                }
            }
            ma[endpos[i]] = val[i];
        }

        if (!res) { // no result
            printf("Case #%d: -1
", kass++);
            continue;
        }

        tree.get_lca();

        for (int i = 1; i <= Discrete::blen; i++) vec[i].clear();
        for (int i = 1; i <= n; i++) {
            vec[val[i]].push_back(i);
        }


        tree.find_lca_init();
        for (int i = 1; i <= Discrete::blen; i++) {
            int lca = endpos[vec[i][0]];
            for (int j = 1; j < SZ(vec[i]); j++) lca = tree.LCA(lca, endpos[vec[i][j]]);
            if (tree.lca_val[lca]) {
                res = 0;    // two value have same lca
                break;
            } else {
                tree.lca_val[lca] = i;
                int k = tree.dep[lca];
                for (auto e: vec[i]) {
                    if (SZ(str[e]) >= k) {
                        //   printf("%d
", tree.T[lca][str[e][k - 1]-'a']);
                        tree.die[tree.T[lca][str[e][k - 1]-'a']] = 1;
                    }
                }
            }
        }

        if (!res) { // no result
            printf("Case #%d: -1
", kass++);
            continue;
        }

        if (!tree.dfs_die(1, 0)) {
            printf("Case #%d: -1
", kass++);
            continue;
        }

        printf("Case #%d: %d
", kass++, tree.solve());

    }
}

/*
4
s 748384849
aeqa 748384849
succk 40574105
a 332084817
 */

#include <bits/stdc++.h>

#define SZ(x) (int)x.size()
using namespace std;
const int MAXN = 1e5 + 5;
const int MAXLOG = 22;
namespace Discrete {
    int b[MAXN], btol, blen;

    void insert(int x) { b[btol++] = x; }

    void init() {
        sort(b, b + btol);
        blen = unique(b, b + btol) - b;
    }

    int val2id(int x) {
        return lower_bound(b, b + blen, x) - b + 1;
    }
}
using Discrete::val2id;


class TRIE {
public:
    int T[MAXN][26], top;

    void init() {
        top = 1;
        memset(T[top], 0, sizeof(T[top]));
    }

    int insert(const string &s, int n) {
        int u = 1;
        for (int i = 0; i < n; i++) {
            int ch = s[i] - 'a';
            if (!T[u][ch]) {
                T[u][ch] = ++top;
                memset(T[top], 0, sizeof(T[top]));
            }
            u = T[u][ch];
        }
        return u;
    }

    int dep[MAXN], fa[MAXN][MAXLOG], lg[MAXN];

    void init(int _n) {
        for (int i = 1; i <= _n; i++) {
            lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
        }
    }


    inline void dfs(int u, int f) {
        fa[u][0] = f, dep[u] = dep[f] + 1;
        for (int i = 1; i <= lg[dep[u]]; i++) fa[u][i] = fa[fa[u][i - 1]][i-1];
        for (int i = 0; i < 26; i++) {
            int v = T[u][i];
            if (v == f) continue;
            if (v) dfs(v, u);
        }
    }

    void get_lca() {
        for (int i = 1; i <= top; i++) memset(fa[i], 0, sizeof(fa[i]));
        dep[1] = 0;
        dfs(1, 1);
    }

    int LCA(int u, int v) {
        if (dep[u] < dep[v]) swap(u, v);
        while (dep[u] > dep[v]) u = fa[u][lg[dep[u] - dep[v]] - 1];
        if (u == v) return u;
        for (int k = lg[dep[u]] - 1; k >= 0; k--) {
            if (fa[u][k] != fa[v][k]) u = fa[u][k], v = fa[v][k];
        }
        return fa[u][0];
    }

    int lca_val[MAXN], die[MAXN];

    void find_lca_init() {
        for (int i = 1; i <= top; i++) lca_val[i] = 0;
        for (int i = 1; i <= top; i++) die[i] = 0;
    }

    int dfs_die(int u, int die_flag) {
        if (die[u]) die_flag = 1;
        if (lca_val[u] && die_flag) return 0;
        for (int i = 0; i < 26; i++) {
            int v = T[u][i];
            if (v) {
                if (!dfs_die(v, die_flag)) return 0;
            }
        }
        return 1;
    }

    int lca_cnt[MAXN], vis[MAXN];

    inline void dfs_ans(int u) {
        int fg = 0;
        for (int i = 0; i < 26; i++) {
            int v = T[u][i];
            if (v) {
                dfs_ans(v);
                lca_cnt[u] += lca_cnt[v];
                if (lca_cnt[v] == 1) {
                    fg = v; //break;
                }
            }
        }
        if (lca_val[u]) lca_cnt[u]++;
        if (!lca_val[u] && fg) {
            vis[u] = 1, vis[fg] = 0;
        } else if (lca_cnt[u]) vis[u] = 1;

    }

    int solve() {
        for (int i = 1; i <= top; i++) lca_cnt[i] = vis[i] = 0;
        dfs_ans(1);
        int ans = 0;
        for (int i = 1; i <= top; i++) ans += vis[i];//, printf("%d
", lca_cnt[i]);
        return ans;
    }


} tree;


string str[MAXN];
int val[MAXN], endpos[MAXN];
vector<int> vec[MAXN];

int main() {
    tree.init(MAXN - 1); // init for lg
    int T;
    cin >> T;
    int kass = 1;
    while (T--) {
        Discrete::btol = 0;
        int n;
        cin >> n;
        for (int i = 1; i <= n; i++) {
            cin >> str[i] >> val[i];
            Discrete::insert(val[i]);
        }
        Discrete::init();
        for (int i = 1; i <= n; i++) val[i] = val2id(val[i]);

        unordered_map<int, int> ma; // same string two val
        int res = 1;

        tree.init();
        for (int i = 1; i <= n; i++) {
            endpos[i] = tree.insert(str[i], SZ(str[i]));
            if (ma.find(endpos[i]) != ma.end()) {
                if (ma[endpos[i]] != val[i]) {
                    res = 0;
                    break;
                }
            }
            ma[endpos[i]] = val[i];
        }

        if (!res) { // no result
            printf("Case #%d: -1
", kass++);
            continue;
        }

        tree.get_lca();

        for (int i = 1; i <= Discrete::blen; i++) vec[i].clear();
        for (int i = 1; i <= n; i++) {
            vec[val[i]].push_back(i);
        }


        tree.find_lca_init();
        for (int i = 1; i <= Discrete::blen; i++) {
            int lca = endpos[vec[i][0]];
            for (int j = 1; j < SZ(vec[i]); j++) lca = tree.LCA(lca, endpos[vec[i][j]]);
            if (tree.lca_val[lca]) {
                res = 0;    // two value have same lca
                break;
            } else {
                tree.lca_val[lca] = i;
                int k = tree.dep[lca];
                for (auto e: vec[i]) {
                    if (SZ(str[e]) >= k) {
                        //   printf("%d
", tree.T[lca][str[e][k - 1]-'a']);
                        tree.die[tree.T[lca][str[e][k - 1]-'a']] = 1;
                    }
                }
            }
        }

        if (!res) { // no result
            printf("Case #%d: -1
", kass++);
            continue;
        }

        if (!tree.dfs_die(1, 0)) {
            printf("Case #%d: -1
", kass++);
            continue;
        }

        printf("Case #%d: %d
", kass++, tree.solve());

    }
}

/*
4
s 748384849
aeqa 748384849
succk 40574105
a 332084817
 */

反思

在赛场上感觉这道题能够贪，但是非常难写，同时卡了很久的博弈和杂题，也就没有思考这道题了。还有一点非常重要就是赛场上没有想到 (LCA) 的重要信息，这就是当时觉得非常难写的原因。

赛后Hartley乱搞就过了，我调了半天还在WA，Hartley给了个转换标记信息做法，就是上面的代码1部分。后来发现是求LCA部分写裂了，~~模板不熟~~。于是就有了两份代码……

对于不存在的情况需要大力讨论，对于 (die) 节点的意义一开始没有想到。

查看全文

相关阅读:
Angular Material Starter App
缺少标识符、字符串或数字
 jquery ajax post 传递数组，多checkbox 取值
 Circular dependencies cannot exist in RelativeLayout
第二次作业
 第一次作业
 第一次作业
 软工实践个人总结
 第01组 Beta版本演示
 第01组 Beta冲刺（4/5）

原文地址：https://www.cnblogs.com/tudouuuuu/p/14016363.html