这几天在看Hadoop的排序,用到了有TotalSortPartition,其中用到了一种叫做trie树的数据结构,每次看到这种自己之前没有听过的数据结构就想去看一下原理,然后再网上看几篇博客,有时间再看一下相关的论文。
trie树,又称为字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构。之前有见到过说多个字符串共用前缀可以节省内存,今天来专门来学习一下这个trie树。
trie这个单词很奇怪,其实它并不是一个独立的单词,而是来自于retrieve的中间部分,retrieve有从中检索、取回的意思。
英文字母的字典树是一个26叉树,数字的字典树是一个10叉树。
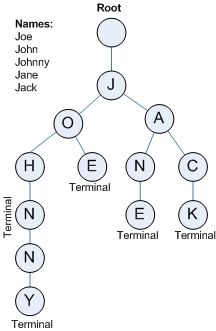
下面直接给出一个trie的例子。
(图片来自Google)
怎么样,给出了一张图片是不是秒懂了trie树,trie树的这种共享公共前缀的方式在某些情况下可以节省很多内存空间,但是如果这些词都没有公共前缀的话,效果就不是很好了。
trie树的性质
(1)根节点不包含字符,除了根节点之外的每个节点都包含一个字符。
(2)从根节点到某一个节点,路径上经过的字符连接起来,即为该节点对应的字符串。
(3)每个节点的所有子节点包含的字符串不相同。(我感觉这条性质可以从性质一推导出来。)
trie树的基本实现
实现方法有以下几种:
1. 对每个节点开一个字符集大小的数组,对应的下标是子节点所表示字母,内容则是这个子节点在大数组上的位置;
2. 每个节点挂一个链表,按一定的规则记录每个儿子是谁;
3. 左儿子右兄弟表示法记录这棵树;(左儿子右兄弟是什么鬼?)
4. 我在想为啥不可以用树来记录这个数据结构呢,trie不是本来就是一棵树么?
trie树的高级实现
可以采用双数组(Double-Array)实现,利用双数组可以大大减少内存的使用量。
trie树的应用
字符串检索
字符串检索,事先将一些字符串(字典)的有关信息保存到trie树中,查找另外一些未知字符串是否出现或者出现的频率。
字符串的最长公共前缀
对给定字典建立trie树之后,求两个串的最长公共前缀长度是多少,就是求最多的公共祖先个数。
并查集(Disjoint Set),可以采用经典的Tarjan算法。Least Common Ancestor,LCA
求出字母树的欧拉序列(Eule Sequence),转为经典的最小值查询,Range Minimum Query,简称RMQ问题
排序
trie树是一颗多叉树,只要前序遍历整棵树,输出相应的字符串便是按字典排序的结果。
在Hadoop的TotalOrderPartitioner中的应用
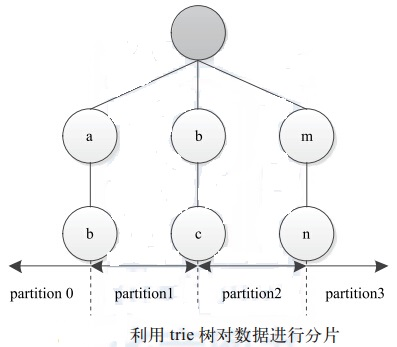
Map 阶段。本阶段涉及两个组件,分别是Mapper和Partitioner。其中,Mapper 可采用 IdentityMapper,直接将输入数据输出,但 Partitioner 必须选用TotalOrderPartitioner,它将上一个步骤中获取的分割点保存到 trie 树中以便快速定位任意一个记录所在的区间,这样,每个Map Task产生R(Reduce Task个数)个区间,且区间之间有序。TotalOrderPartitioner 通过trie树查找每条记录所对应的Reduce Task编号。如图所示, 我们将分割点保存在深度为2的trie树中,假设输入数据中有两个字符串"abg"和"mnz",则字符串"abg"对应partition1,即第2个Reduce Task,字符串"mnz"对应partition3,即第4个Reduce Task。
作为其他数据结构和算法的辅助结构
后缀树,AC自动机等。
Trie树是一种非常重要的数据结构,它在信息检索,字符串匹配等领域有广泛的应用,同时,它也是很多算法和复杂数据结构的基础,如后缀树,AC自动机等,因此,掌握Trie树这种数据结构,对于一名IT人员,显得非常基础且必要!
(1)wiki:http://en.wikipedia.org/wiki/Trie
(2) 论文《浅析字母树在信息学竞赛中的应用》
(3) 论文《Trie图的构建、活用与改进》
(4) 博文《An Implementation of Double-Array Trie》:
http://linux.thai.net/~thep/datrie/datrie.html
(5) 论文《An Efficient Implementation of Trie Structures》:
http://www.google.com.hk/url?sa=t&source=web&cd=4&ved=0CDEQFjAD&url=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Fdoi%3D10.1.1.14.8665%26rep%3Drep1%26type%3Dpdf&ei=qaehTZiyJ4u3cYuR_O4B&usg=AFQjCNF5icQbRO8_WKRd5lMh-eWFIty_fQ&sig2=xfqSGYHBKqOLXjdONIQNVw
(6)数据结构之Trie树