树杂谈(上)
研究问题的道路,一般都是从特殊到一般,从简单到复杂。在数学中,三角形是一种特殊的多边形,因此在三角形的基础上,又有了有关全等三角形、相似三角形、三角函数等令学生们头疼的数学题。同样的道理,在信息学竞赛的道路上,树——作为一种最特殊的图,在许多题目中都能见到它的身影。
1. 树的基本概念和一些有关定义
树的基本概念
本人见过的一种比较简洁的定义是:
由 (n) 个点,(n - 1) 条边组成的无向连通图称为树。
树分为有根树和无根树。下文所有的树未经说明,均指有根树,且树的根为 1 号节点。
根据这个定义,这是树:
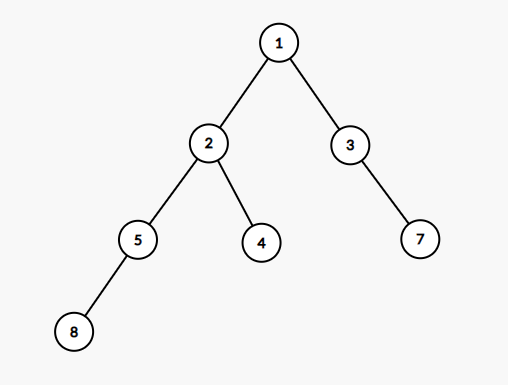
事实上,这是一种比较特殊的树,称为「二叉树」。「二叉树」的特点在于每个节点最多只与三个节点相连,因此对于某个节点 (v),除去它的父亲节点,最多只有两个儿子,我们称之为左儿子 (lson) 和右儿子 (rson)。这个条件是非常类似于分治的时候,将某一段区间 ([l, r]) 分为 ([l ,mid]) 和 ([mid , r]) 的过程,所以我们可以递归地去处理二叉树的子树信息,并用父节点维护(事实上,我习惯把分治的递归过程抽象成树上的遍历过程)。所以,二叉树被用于作为一些高级数据结构的实现方式。
此外,比较特殊的树还有「链」和「菊花」。
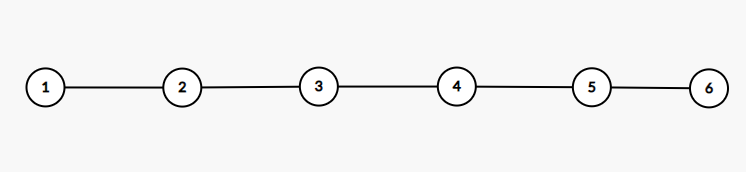
这是一个链的例子。链的特点在于每一个点最多只与两个节点相连。
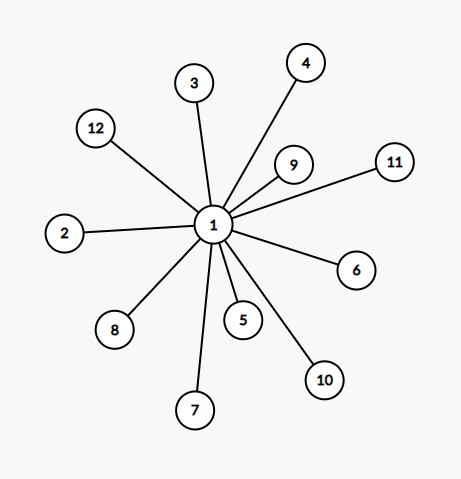
这是一个菊花的例子。菊花的特点在于有 (n - 1) 个点都只和 (1) 个点相连,而有一个点和 (n - 1) 个点相连。
树其实是一种特殊的无向图。如果再仔细思考,不难发现,如果有 (n) 个点,想要连通(即对于任意两个点 (u) 和 (v),都至少有一条 (u) 到 (v) 的路径),至少要加 (n - 1) 条无向边——刚好形成一棵树。利用树的这个性质,在日常生活中,倘若要花最少的钱来修筑道路,那么道路的设计方案就是一棵树的形状。
此外,由于树是最简单的一种图,如果我在树上不相邻两个节点间增加一条无向边(相邻算作重边),那么必然会出现环。如下图所示。

我翻遍了网络,很难找到一个对于无向图的环的准确定义。最终找到 CF977E,那里对于无向图的环的定义我认为比较严谨:
环 (cycle):原图中存在一个含有 (m) ((m ge 3)) 个点的点集 (V'),存在一个含有 (m) 条边的边集 (E'),使得点集 (V') 和边集 (E') 经过重新排序,可以满足:
- (V'_1) 与 (V'_2) 通过边 (E'_1) 相连。
- (V'_2) 与 (V'_3) 通过边 (E'_2) 相连。
- ……
- (V'_m) 与 (V'_1) 通过边 (E'_m) 相连。
只有满足这些条件,我们才称这个子图 (G' = {V', E'}) (点集和边集)为环。环既包含了点,也包含了边。
因为没有环,对于树上任意两点 (u) 和 (v),它们之间只会存在一条简单路径(即每条边只经过一次的路径)。因此,对于树上的两点间最短路径,其实就是两点间唯一的这条简单路径,可以做到很快速地进行查询,无需最短路径算法。这也是树很重要的一个性质,在竞赛中常常会出现。
树相关的定义
树根:有根树深度为 (0) 的点,一般画在树的最上面。对于无根树,可以任选一个节点设其为根。
父亲:与之相邻的,距离它离根节点更近的点称为该节点的父亲节点。如上图二叉树,(3) 号节点是 (7) 号节点的父亲。注意:父子关系会随着根的变化而变化。
深度:如果我们把某个节点(一般使用节点 (1))作为树的根,那么按照每一个节点到根距离的远近,我们赋给每个节点一个深度 (depth),表示这个节点与根节点的简单路径上的边数。比如对于上面的二叉树,(1) 号点是根节点深度为 (0),(3) 号点的深度是 (2),(4) 号点的深度是 (3),(8) 号点的深度是 (4)。
子树:对于某个点 (v),包括它自己在内的,有一个祖先(父亲、父亲的父亲、父亲的父亲的父亲……)是 (v) 的点,连同连接它们的所有边构成的集合,称为节点 (v) 的子树。比如对于上面的二叉树,(2) 的子树就是 (2, 5, 4, 8) 和连接它们的那三条边 (2 leftrightarrow 5, 2 leftrightarrow 4, 5 leftrightarrow 8)。
大小:子树内包含的点数。如上图二叉树中,(2) 号节点的大小为 (4)。
2. 生成树
我们介绍了,想要使得一个 (n) 个点的图连通,至少需要 (n - 1) 条边。也就是说,树的图连通的最基础的情况。这个特性在生活中的应用很多。
20 世纪早期,有一家电力公司希望架设电线。一共有 (n) 根电线杆,由于电线杆间距离远近等差异,两两电线杆间架设电线的花费不同。电力公司的员工们希望花费最少的钱将所有电线杆连通。
这是一个真实的故事。事实上,这就是一个最经典的最小生成树问题。用计算机的语言来表述,就是:
一共有 (V) 个点,(E) 条无向边,第 (i) 条边连接 (u_i) 和 (v_i),需要花费 (w_i) 来添加,求使整张图连通的最小花费。(保证图连通)
当时的人们找到著名数学家 Otakar Borůvka 来解决这个问题。Borůvka 想了一会儿,便想到了如今被称为 Borůvka 算法的最小生成树算法(由于此时计算机还未发明,在之后,计算机学家 Sollin 将这种算法引入了计算机领域,故又称 Sollin 算法)。这是我所知道的最早的最小生成树算法的应用。
如今,最小生成树算法有许多。比较流行的是 Kruskal 和 Prim 算法,还有毒瘤出题人爱考的 Borůvka 算法。
以下代码对应洛谷的最小生成树模板题。
Kruskal 算法
我们已经知道,树是图连通最基础的情况,因此,为了生成一棵树,我们只需要在没有多余边的情况下,让这些点连通即可。什么时候的边会成为多余的呢?当且仅当这条边所连接的两个端点,已经直接或间接连通。
Kruskal 主要执行流程如下:
- 将所有边按照权值(花费)大小排序。
- 从权值小的边开始加边。若该边不是多余的边(连接的两个点不属于一个连通块),则将该边加入,将两边连通块并在一起。
这样最终得到的图就是最小生成树,也就是所有边的权值和最小。
证明可以意会:对于这样生成的树中的某一条边 (e),假设存在一条非树边 (e'),满足将 (e') 替换掉 (e) 后最小生成树权值更小。那么 (w_{e'} < w_e),显然排序我会先加 (e') 边才加 (e) 边。如果 (e') 边没加入,则说明 (e') 边多余,那么它能替换 (e),则说明 (e) 也多余,是矛盾的。故这样生成的树是最小生成树。
连通块可以使用并查集的方法进行维护,代码不难写。时间复杂度为 (O(E log E +E log V))。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MaxN = 5000 + 5, MaxM = 200000 + 5;
struct edge {
int u, v, w;
};
int N, M;
int par[MaxN];
edge E[MaxM];
void init() {
scanf("%d %d", &N, &M);
for (int i = 1; i <= M; ++i)
scanf("%d %d %d", &E[i].u, &E[i].v, &E[i].w);
}
inline bool cmp(edge x, edge y) {
return x.w < y.w;
}
int Find(int x) {
if (x == par[x]) return x;
else return par[x] = Find(par[x]);
}
void solve() {
for (int i = 1; i <= N; ++i) par[i] = i;
int ans = 0;
sort(E + 1, E + 1 + M, cmp);
for (int i = 1; i <= M; ++i) {
int u = E[i].u, v = E[i].v, w = E[i].w;
int p = Find(u), q = Find(v);
if (p != q) {
ans += w;
par[p] = q;
}
}
cout << ans << endl;
}
int main() {
init();
solve();
return 0;
}
Prim 算法
Prim 算法是一种贪心算法。我们知道,作为一棵最小生成树,每个节点都应该被连进树中。那么我们就可以随意找一个节点加入集合,每次取集合内向集合外的权值最小的边,不断向外扩张树的大小,知道所有点都被加入集合。
这种算法的执行流程与 Dijkstra 类似,但是可以正确处理负权边的情况。寻找权值最小的边的过程可以使用堆或优先队列进行优化。时间复杂度可以做到 (O(E log E))。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef pair <int, int> pii;
const int MaxN = 5000 + 5, MaxM = 400000 + 5;
int N, M; int cnte;
int Head[MaxN], To[MaxM], Next[MaxM], Val[MaxM];
bool vis[MaxN];
priority_queue < pii, vector<pii>, greater<pii> > pq;
inline void add_edge(int from, int to, int val) {
cnte++; To[cnte] = to; Val[cnte] = val;
Next[cnte] = Head[from]; Head[from] = cnte;
}
void init() {
scanf("%d %d", &N, &M);
for (int i = 1; i <= M; ++i) {
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
add_edge(u, v, w);
add_edge(v, u, w);
}
}
void prim() {
int ans = 0;
vis[1] = true;
for (int i = Head[1]; i; i = Next[i]) pq.push(make_pair(Val[i], To[i]));
while (!pq.empty()) {
pii p = pq.top(); pq.pop();
int u = p.second;
if (vis[u] == true) continue;
vis[u] = true; ans += p.first;
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i], w = Val[i];
if (vis[v] == false) pq.push(make_pair(w, v));
}
}
cout << ans << endl;
}
int main() {
init();
prim();
return 0;
}
Borůvka 算法
这个算法的教程在网上极少…… 翻了好多的博客都没理解,最终找到了维基百科的 Borůvka's algorithm 词条,终于弄懂了这个十分古老的算法。
Borůvka 其实是一种多路增广的 Prim。Prim 算法由一个点开始,往外不断贪心地找最短边,然后不断扩大连通块,直到形成一棵树。而 Borůvka 算法每一次的增广,会对现在的每一个连通块都找一遍的最短边,最后每个连通块择优,将这些边全部连上。
算法的执行流程大约是这样的:
- 对于现在的每个连通块,找到从这个连通块出发,不在最小生成树中的、到达别的连通块的最短边。(特别注意:若权值相同,则需要再按照另一个维度严格排序,常用标号大小排序。即边权相同时,认为编号小的边短。这样处理是为了避免两个连通块互相连的时候出现环)
- 全部找完后,将这些边加入最小生成树中。(可能出现两个连通块互连的情况,那么这时在第一个连通块连完这条边后,标记一下,说明该边已被加入最小生成树,下一次弹掉即可)
利用维基百科的样例可以形象地说明如上步骤:

这样,每一次合并的 (O(E)) 的,但是每一次合并后,连通块的个数都减少一半。这样一来,只要 (log V) 次,就能合并成最小生成树了。所以总时间复杂度是 (O(E log V)) 的。Borůvka 的优势也正在此,它只需要 (log V) 次的合并,这是另外两个 MST 算法所难以达到的。因此,一旦有题目想考察 Borůvka 算法,一定跟这个特性密切相关。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int MaxN = 5000 + 5, MaxM = 200000 + 5;
int N, M;
int U[MaxM], V[MaxM], W[MaxM];
bool used[MaxM];
int par[MaxN], Best[MaxN];
void init() {
scanf("%d %d", &N, &M);
for (int i = 1; i <= M; ++i)
scanf("%d %d %d", &U[i], &V[i], &W[i]);
}
void init_dsu() {
for (int i = 1; i <= N; ++i)
par[i] = i;
}
int get_par(int x) {
if (x == par[x]) return x;
else return par[x] = get_par(par[x]);
}
inline bool Better(int x, int y) {
if (y == 0) return true;
if (W[x] != W[y]) return W[x] < W[y];
return x < y;
}
void Boruvka() {
init_dsu();
int merged = 0, sum = 0;
bool update = true;
while (update) {
update = false;
memset(Best, 0, sizeof Best);
for (int i = 1; i <= M; ++i) {
if (used[i] == true) continue;
int p = get_par(U[i]), q = get_par(V[i]);
if (p == q) continue;
if (Better(i, Best[p]) == true) Best[p] = i;
if (Better(i, Best[q]) == true) Best[q] = i;
}
for (int i = 1; i <= N; ++i)
if (Best[i] != 0 && used[Best[i]] == false) {
update = true;
merged++; sum += W[Best[i]];
used[Best[i]] = true;
par[get_par(U[Best[i]])] = get_par(V[Best[i]]);
}
}
if (merged == N - 1) printf("%d
", sum);
else puts("orz");
}
int main() {
init();
Boruvka();
return 0;
}
Kruskal 重构树
严格来说,Kruskal 重构树求出来的树并不是该图的一棵生成树,它最终求出来的树的点数是 (V imes 2 - 1) 的。Kruskal 重构树执行的过程与最小生成树的 Kruskal 算法类似:
- 将原图的每一个节点看作一棵子树。
- 合并两棵子树时,通过并查集找到它们子树对应的根节点,记作 (u), (v)。
- 新开一个节点 (p),从 (p) 分别向 (u), (v) 两点连边。于是 (u) 和 (v) 两棵子树就并到了一棵子树,根节点就是 (p)。
这样子,如果我们把 (p) 点的权值赋为 (u leftrightarrow v) 这条边的权值,那么我们建出的这一棵树就可以满足如下性质:
- 这是一个大根堆(对应最小生成树的情况,最大生成树为小根堆)。
- 原最小生成树上 (u) 到 (v) 路径上的最大值,就是 (u), (v) 的最近公共祖先(LCA)的权值。故求最小瓶颈路时,可以使用 Kruskal 重构树的方法。
生成树只是树论中的一小部分,但是对于一些题目,如果能够找到一些贪心策略,将普通的图通过生成树的方法转化为特殊的树,那么问题将会简单许多。
3. 最近公共祖先
终于重启这个项目了……由于咕咕咕太久了,码风都变了,望谅解……
最近公共祖先的定义与性质
首先,什么是最近公共祖先(Lowest Common Ancestor,简称 LCA)呢?
给定一个有根树。对于任意的两个点 (u), (v),存在一个点 (x) , 使得 (x) 既是 (u) 的祖先节点(包括自身),也是 (v) 的祖先节点。满足条件的深度最大的 (x) 即为 (u) 和 (v) 的 LCA。
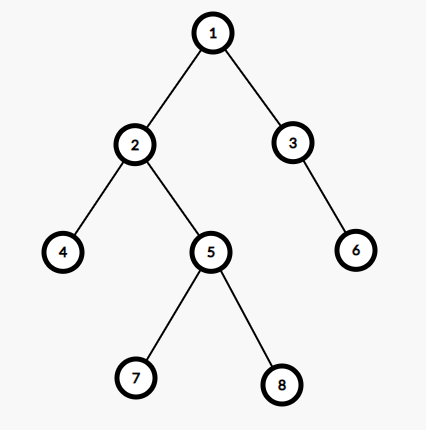
举个例子。对于上图中的树,以 (1) 号点为根,(4) 号点和 (7) 号点的 LCA 是 (2) 号点,(3) 号点和 (8) 号点的 LCA 是 (1) 号点,(5) 号点和 (8) 号点的 LCA 是 (5) 号点,(4) 号点和 (4) 号点的 LCA 是自己——(4) 号点。
感觉 LCA 这个东西好特殊呀,在平常做题时会涉及到关于 LCA 的知识吗?
真的会碰到……而且非常经常遇到 LCA 的题目,近几年 NOIP 提高组特别常出。
这是为什么呢?LCA 有什么神奇的性质吗?
有。观察原树,我们不难发现:
对于树上的任意两点 (u), (v),记它们的最近公共祖先为点 (x),那么在 (u) 到 (v) 唯一的简单路径上,(x) 是深度最小(离根节点最近)的点,且该路径可以被拆分成 (x o u), (x o v) 的两条链。
那么 LCA 就可以用来做树上求最短路径权值和、树上差分……
同时求解 LCA 所用算法的一些思想也是树论题目常常会用到的。比如倍增、DFS 序……所以差不多可以说,LCA 是树论的基础。
所以掌握 LCA 是非常重要的。
倍增算法
以下代码对应洛谷的 LCA 模板题。
倍增是求 LCA 最常用的方法之一。它可以在 (O(n log n)) 的时间内求出某两点的 LCA。此外它还具有代码简洁机动灵活,维护信息种类多的优点。当大家遇到求 DAG 的支配树时,会遇到一棵树动态加点的情况(即在一个节点下连出一个新节点),此时由于没有破坏原树的祖先关系,仍然可以用倍增求 LCA。
我们不难想到一个最最朴素的求 LCA 方法。
对于两个点 (u), (v),可以先将 (u), (v) 跳到同一深度,然后再一步一步往上跳动。当 (u) 和 (v) 重合时,所重合的点就是它们的 LCA。
代码大致上可以这么实现:
int getLca(int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
while (dep[u] != dep[v]) u = fa[u];
while (u != v) {
u = fa[u];
v = fa[v];
}
return u;
}
这种代码的正确性是很好理解的。将 (u), (v) 跳到同一深度的目的就是要保证当它们所在子树在 LCA 处合并时,它们都能跳到当前子树的根的位置——也就是 LCA 的位置。但是这样的复杂度是 (O(n^2)),不可接受。但是我们可以使用倍增这种数据结构来优化它。
相信大家都写过快速幂。
// 求 low ^ high
inline int Fast_pow(int low, int high) {
int res = 1;
while (high > 0) {
if (high % 2 == 1) res *= low;
high /= 2;
low = low * low;
}
return res;
}
其实快速幂就是倍增的一种经典运用。我们试着换一种长得更“倍增”的写法。
// Pow[i] 存储 low ^ (2 ^ i) 的值
int Pow[MaxLog];
inline int Fast_pow(int low, int high) {
Pow[0] = low;
for (int i = 1; (1 << i) <= high; ++i)
Pow[i] = Pow[i - 1] * Pow[i - 1];
int res = 1;
for (int i = 0; (1 << i) <= high; ++i)
if (high & (1 << i)) res = res * Pow[i];
return res;
}
由上面代码我们看出,当 (high) 特别大的时候,数组可能无法存下所有的值。但是我们可以只存 (2^0), (2^1), (dots), (2^n) 的值,这样只会有 (log high) 个。并且,如果我们知道了 (low^{x}) 的值(即 (Pow_{log_{2} x}) 的值),那么我们可以直接通过 (low^{x imes 2} = (low^x)^2) 的公式来求出 (Pow_{log_{2} x+ 1}) 的值。于是我们可以在 (O(log high)) 内求出这个 (Pow) 数组。
我们知道了 (Pow) 数组的值以后,有什么用呢?其实,如果把原来的十进制数 (high) 看成一个二进制数,就可以将 (high) 变成 (2^n imes a_n + 2^{n - 1} imes a_{n - 1} + dots + 2^0 imes a_0),其中 (a) 数组值只会是 (0) 或 (1),它可以通过位运算求出来。那么我们用这个冗长的式子代入到 (low^{high}) 当中,
因此对于每一个 (i) ((0 le i le n)),如果对应的 (a_i) = 0,那么这个乘积就是 (0),这个位置的值 (low^{2^i imes a_i}) 就等于 (2^0) 即 (1),对最终的乘积不会有贡献。反之,如果这个地方 (a_i = 1),那么这里的值就是 (low^{2^i imes a_i} = low^{2^i}),其实就是我们求出的 (Pow_i)。直接将积乘上 (Pow_i) 即可。
这个基本就是倍增的主要思路。即对于非常多的步骤,我们只做 (2^0, 2^1, dots, 2^k) 这些步骤。一般我们都能求得第一个步骤(即 (2^0))的值,再通过递推将其推到 (k)。最后查询直接查原数的二进制位对应的值,合并起来即可。这样我们可以把暴力 (O(n)) 的复杂度降至 (O(log n))。
通过快速幂,我们也能看到,这些步骤可以用倍增维护,必须满足:
- 操作静态。
- 步骤可以合并。即满足结合率。
我们看一下这个倍增算法是如何应用到求 LCA 上的。
我们使用朴素算法求 LCA 的时候,我们需要将点 (u) 跳到它的父亲,再跳到它的父亲的父亲,再跳到它的父亲的父亲的父亲……这样无疑太浪费时间了。我们希望能够缩小它跳的次数,但是又不能直接存下它往上任意 (d) 步回调到哪个点(也就是它的 (d) 次祖先),因为这太浪费空间了。
类似快速幂的思路,我们可以预处理出每个点向上跳 (2^0, 2^1, 2^2, cdots, 2^{log n}) 次所能跳到的点。
对于朴素算法的第一步:把 (u) 和 (v) 调整至同一深度。这是不难用倍增优化的。(u) 和 (v) 的深度差是一个确定的值 (d),那么对 (d) 进行二进制分解,倍增跳动就好了。
对于第二步:不断向上跳动直至重合。在做这一步的时候,我们不知道要跳几步。但是有一种很简单的跳动策略:我们只需要从高到低,每一种跳动都试过去。如果跳过了不重合,那么就跳,否则不跳,最后 (u), (v) 两个点所在的位置就是它们 LCA 的两个儿子。
这是因为设我们需要跳动的次数为 (d),设其最高位为 (i),若我们尝试跳 (2^{i +1}) 步,由于 (2^{i +1} > d),那么这两个点一定会超过或者刚好在 LCA 的位置,导致二点重合。因此我们从高到低枚举的第一位在 (d) 上一定是 (1)。或者也可以这么理解,如果我在 (d) 上不跳最高位上的 (1),那么后面再怎么跳也跳不到这个点,这基于一个很简单的结论:(2^i > 2^i - 1 = 2^{i - 1} + 2^{i - 2} + cdots + 2^0)。
最后有一些实现上的细节:
-
每个节点的深度可以用一次 DFS 快速求出。它们跳 (2^i) 所能跳到的点也可以在这次 DFS 中完成,这就类似于一个 DP 的过程。记 ( exttt{fa[i][v]}) 表示 (v) 向上跳 (2^i) 步到达的点,那么它向上跳 (2^{i + 1}) 步到达的点就是它向上跳 (2^i) 步,再向上跳 (2^i) 步到达的点,即 ( exttt{fa[i + 1][v] = fa[i][fa[i][v]]})。
-
最后求得的 LCA 是最终 (u) 和 (v) 所跳到点的父亲,因为到 LCA 的时候我们会判作两点重叠,不跳。
-
第一步跳动结束,如果 (u) 和 (v) 已经相等了,那么应该直接返回 (u) 或 (v),否则会返回它们的父亲。
由于用到倍增数组,空间复杂度为 (O(n log n));
预处理倍增数组需要 (n log n) 的复杂度,有 (q) 次询问,每次倍增最短跳动 (log n) 次,则总时间复杂度为 (O((n + q) log n))。
以下是代码实现:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int MaxN = 500000 + 5, MaxM = 1000000 + 5;
const int MaxLog = 20;
int N, M, rt; int cnte;
int Head[MaxN], To[MaxM], Next[MaxM];
int fa[MaxLog + 1][MaxN], dep[MaxN];
inline void add_edge(int from, int to) {
cnte++; To[cnte] = to;
Next[cnte] = Head[from]; Head[from] = cnte;
}
void init() {
scanf("%d %d %d", &N, &M, &rt);
for (int i = 1; i < N; ++i) {
int u, v;
scanf("%d %d", &u, &v);
add_edge(u, v); add_edge(v, u);
}
}
void dfs(int u) {
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i];
if (v == fa[0][u]) continue;
dep[v] = dep[u] + 1;
fa[0][v] = u;
for (int j = 1; (1 << j) <= dep[v]; ++j)
fa[j][v] = fa[j - 1][fa[j - 1][v]];
dfs(v);
}
}
inline int getLca(int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
int d = dep[u] - dep[v];
for (int i = 0; i <= MaxLog; ++i)
if (d & (1 << i)) u = fa[i][u];
if (u == v) return u;
for (int i = MaxLog; i >= 0; --i)
if (fa[i][u] != fa[i][v])
u = fa[i][u],
v = fa[i][v];
return fa[0][u];
}
void solve() {
dfs(rt);
for (int i = 1; i <= M; ++i) {
int u, v;
scanf("%d %d", &u, &v);
printf("%d
", getLca(u, v));
}
}
int main() {
init();
solve();
return 0;
}
应用
以下题目若无特殊说明,(n, q) 均在 (10^5) 级别。
树上前缀和
给定一个 (n) 个点,(n-1) 条边的无向连通图,边上有权值。并有 (q) 次询问,每次询问输入两个数 (u), (v),查询从点 (u) 到点 (v) 的最短路径长度。
(n) 个点,(n - 1) 条边的无向连通图,其实就是一棵树。考虑使用有关树的算法求解。
因为本题边的值是确定的,没有修改操作。考虑使用前缀和,快速查询树上区间和。
因为树上最短路径是唯一的,可以随便找一个点作为根节点,把这棵无根树转化为有根树。习惯上,将 (1) 号节点作为根。对于每一个节点 (u),维护一个数组 (pre_u),表示从 u 点到根节点的最短路径权值和。这个可以直接用一次 DFS 算出。
对于查询树上 (u), (v) 两点间距离,我们发现,其最短路径上一定会经过这 (u) 和 (v) 的 LCA,且 LCA 必定为所经过点中深度最小的点。于是我们可以将 (u) 到 (v) 的最短路径拆成两部分:从 (u) 到 LCA 的最短路径和从 (v) 到 LCA 的最短路径。而这些可以利用前缀和高效求得。即 (dis_{u, v} = pre_u + pre_v - 2 pre_{lca(u, v)})。
时间复杂度 (O((n +q) log n))。
树上差分
给定一棵 (n) 个点,(n - 1) 条边的无向联通点权图。开始时所有点权均为 (0)。现有 (q) 次操作,每次操作将 (u) 到 (v) 的最短路径上的所有点的权值 (+1)。全部操作结束后,问权值最大的点权值是多少。
最后才查询,考虑树上差分。
使用一个差分数组 (dif),(dif_i) 是 (i) 到根节点的这一条链上的差分数组,即 (dif_i = a_i - a_{fa_i})。
从 (u) 到 (v) 的最短路径可以拆成从 (u) 到 LCA 的最短路径和 (v) 到 LCA 的最短路径。于是变成只要在两条链上区间加,直接执行 ( exttt{dif[u]++; dif[v]++; dif[lca]--; dif[fa[lca]]--;})(因为是点权图)即可。最后查询时从下往上还原出所有点的点权 (a_i)。方法是 (a_i = left(sum_{j in son_i} a_j ight) + dif_i)。
时间复杂度 (O((n + q) log n))。
给定一个 (n) 个点,(n - 1) 条边的无向连通图。每条边有权值。另外有 (m) 组最短路询问。现可以将任意一条边的权值变为 (0),使最长的最短路径长度最短。并求出这个最短路径值。
经典的二分套路:使得最大值最小。
我们可以用树上前缀和先做一遍树上最短路。
判断答案为 (x) 时可不可以完成。显然,我只要对原来最短路长度大于 (x) 的最短路询问,将这条路径上的某一条路径变为 (0)。而且变成 (0) 的这条路径是要所有长度大于 (x) 的最短路询问都有经过的一条路径。
树上差分找出所有满足条件的路径。一一判断能否在 (x) 内完成即可。
由于本题会有点卡常数,建议使用一些较快的 LCA 算法,如 Tarjan 算法或树剖。
时间复杂度 (O(m log m + (n + m) log n))。
维护两点间路径最小/最大值
给定一个 (n) 个点,(m) 条边的无向图,边上有权值。并有 (q) 次询问,每次询问输入两个点 (u), (v),找出一条路径,使得从 (u) 到 (v) 路径上的最小值最大,并输出这个最大的最小值;若从 (u) 不能到达 (v),输出 (-1).
直接使用并查集来判断是否 (u), (v) 两点是否连通。
但原图不是一棵树怎么办?可以证明:所走路径一定在最大生成树上。
于是原题转化为了树上问题。
Kruskal + 倍增维护路径最小值。直接在 DFS 找父亲的时候顺便 DP 合并一下路径最小值就好了。
Kruskal 重构树以后,直接询问 (u), (v) 两点的 LCA 的点权也是可以做的。我认为这种做法更好写一些。
时间复杂度 (O(m log m + (n + q) log n))。
给定 (n) 个点,(m) 条边,求其严格次小生成树的各边权值和。
注:严格次小生成树是指各边权值和小于最小生成树且大等于其它生成树。
先求出最小生成树。
然后枚举每一条非树边,加上这条非树边后,则必然在原图中形成环,且这个环是由这条非树边两端点的最短路构成的。我们使其替换这个环内的一条边满足这条非树边的权值大于被替换的边,更新答案最小值。
一个显然的贪心:每次替换一定替换最大的且与该边权值不相等的边。
倍增维护路径最大值与严格小于最大值的次大值。若路径最大值与该非树边权值相等,则替换次大边。否则替换最大边。
时间复杂度 (O(m log m + (n + m) log n))。
另外的启示
给出一个 (n) 个节点的有根树(编号为 (0) 到 (n-1),根节点为 (0))。一个点的深度定义为这个节点到根的距离 (+1)。 设 (dep_i) 表示点 (i) 的深度,(lca_{i, j}) 表示 (i) 与 (j) 的最近公共祖先。有 (q) 次询问,每次询问给出 (l), (r), (z),求 (sum_{i = l}^ r dep_{lca_{i, z}})。
这题正解需要写树剖,但思路却给了我们一个启示。
求 (u) 和 (v) 的 LCA,可以理解为把 (u) 到根节点路径上所有节点染上一个颜色,然后让 (v) 向上走,走到的第一个有颜色的点就是 (u) 和 (v) 的LCA。
同理可以拓展到求LCA的深度,也就是求从 (v) 到根节点的路径上有多少个点被染色。
总结
树论作为近年来 NOIP 的热门话题(NOIP2018 甚至出了三道树题),最近公共祖先作为其中最基础的数据结构,是必然要深刻理解且熟练掌握的。这样在考场上遇到树论题时,才能驾轻就熟,举重若轻。
4. 树链剖分
树链剖分主要有三种,它们分别应用于不同的领域:
- 重链剖分
- 长链剖分
- 实链剖分
重链剖分一般用于动态维护树上路径的信息;长链剖分可以用于 (O(1)) 求 (k) 级祖先,也可以合并某些相邻子树的信息;实链剖分用于 LCT。由于博主太弱了,不会长链剖分,而实链剖分等后面的 LCT 时候再介绍,所以这里就只介绍重链剖分。
实际上,树链剖分 通常情况下 在狭义上指的就是重链剖分。由于我一些劣习改不过来 因此下文中可能会出现混淆着使用的情况,希望大家谅解。
利用 LCA + 前缀和的技巧,我们已经掌握了静态维护树上信息了。但是这还远远不能 应对出题人的毒瘤 满足我们的需求。因此,我们考虑如何动态处理树上的一些信息。
引入
先来简单的——维护子树信息。
有一棵 (n) 个点的树,以 (1) 为根,你有 (m) 次操作,每次操作可以将一个点 (x) 对应的子树加上一个值 (v),或者询问点 (x) 所在子树的权值和。(n, m le 10^5)。
注:点 (x) 对应的子树是指在原树的所有子树中,以 (x) 为根的那棵子树。
直接维护树上信息显然不容易维护。但是我们已经会使用线段树来维护序列上的区间信息了。我们不妨试试,能不能把子树信息转化为区间信息来维护?
不难想起树的 DFS 序。在树的 DFS 序中,一棵子树一定是一段连续的区间,这是因为访问到一个点后,必须得把它的所有子树全部访问过后才能返回,于是它的子树就是连续地遍历着,对应到 DFS 序上就是一段连续的区间。那么我们先求出整棵树的任意一个 DFS 序,之后用线段树区间修改区间查询处理一下就可以了。
时间复杂度 (O(n + m log n))。
但是如何维护链上信息呢?
相信你应该从维护子树信息的做法上得到了一点启示——能不能把某条路径的信息转换成区间信息来维护呢?
答案是肯定的。
原理
顾名思义,将一棵树链上的信息转化为区间信息的过程,叫做树链剖分。
我们还是考虑求出这棵树的 DFS 序,但这次 DFS 的过程要有特点,我们希望一条链的信息连在一块。
但我们很快发现一个问题:一个点可能属于多条树链。也就是说,一条链的信息无法简单地用一个区间表示。
那看来只能用多个区间表示了……看来时间复杂度又要退化到 (n^2)……
别灰心。我们还是寄希望于找到一种 DFS 序,使得分成的区间尽量少。
这是可行的。树剖就是这么一种操作,它能保证分成的区间不超过 (log k) 个。
我们将这棵树的 (n - 1) 条边划分为轻边和重边。保证每个非叶节点向下只会有一条重边,且重边连向的儿子是该节点的所有儿子中,子树大小最大的那个儿子。我们称这个儿子为重儿子,该点其它儿子为轻儿子。
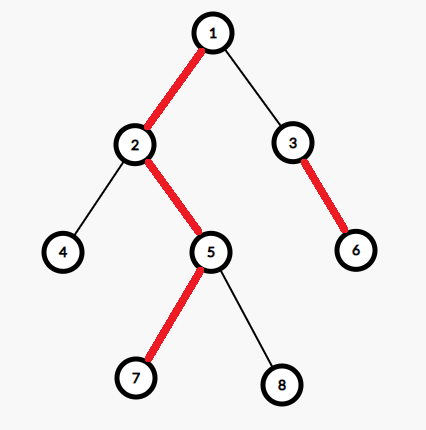
举个例子。对于上图的树,重边已用红色加粗标出。其中 (2) 是 (1) 的重儿子,(6) 是 (3) 的重儿子,(5) 是 (2) 的重儿子,(7) 是 (5) 的重儿子。对于每个叶子节点,都没有重儿子。
可以看出,树上所有的重边,有的会首尾相接,于是形成了在原树上深度严格递增的若干条链。我们称这些链为重链。一条重链深度最低的点我们成为链头。比如对于上图 (1 o 2 o 5 o 7) 这条是重链,链头为 (1),(3 o 6) 这条也是重链,链头为 (3)。对于叶子节点,自己就是一条重链。比如说 (4) 是一条重链,链头为 (4);(8) 也是一条重链,链头为 (8)。
我们从这种轻重边划分中,会发现一些性质:
- 每个节点都属于一条重链。
- 一条轻边一定连接着某一条重链的链头和另一条重链的某一个节点。我们可以用分类讨论的思想来证明。1) 对于某条重链链头引出的一条轻边,由于树没有环,那么这条边一定连向另一条重链的某一个节点。2) 对于重链上某个点连出的一条轻边,根据 dfs 的性质,它所连的点一定是在访问重链上这个点时,还未访问过的点。因此这个点会变成该点所在子树的根。所以就一定会作为一个链头,往子树中牵下去一条重链。
- 从某个节点到根,路径一定会是轻边和重链交错出现,不可能连续有两条轻边。即一定长成一条重链的一部分 ( o) 轻边 ( o) 一条重链的一部分 ( o) 轻边 ( o) …… ( o) 最后一条重链的链头(即根节点)。
- 该点到根节点的路径上,最多只有 (log n) 条轻边。这是因为:假设当前重链链头为 (u),(u) 的父亲为 (f),(f) 的重儿子为 (v)。根据定义,之所以 (v) 会成为 (f) 的重儿子,是因为 (v) 的子树大小大等于 (u),即 (size_v ge size_u)。那么由于 (size_f > size_v +size_u),所以 (size_f > 2 cdot size_u)。所以每走一次轻边,子树大小至少翻番。由于树的点数只有 (n) 个,因此最多翻 (log n) 次,即最多走 (log n) 条轻边。
- 同样,这条路径上,最多只有 (log n) 条重链。因为重链和轻边交错出现,因此级别是相同的。
到根节点有这种性质,到其它节点同理,都会有这种性质。
于是我们发现,通过重链剖分,我们把树上的任意一条路径,拆成了 (log n) 条的重链。这每条重链的所连接的点,深度严格递增,因此我们可以通过调整 DFS,使得重链上的点编号连续,在 DFS 序上形成从左至右深度连续递增的一段区间。
这样,对于每一次路径操作,我们只需要进行 (log n) 次的区间操作就行了。因此复杂度是 (O(n log^2 n)) 的。但实际运行中,树剖的复杂度很优秀。在随机化数据中,平均只会被分成 (log log n) 个区间,因此复杂度大致可以做到 (O(n log n log log n))。(至于为什么我也不会证)
代码实现
以下代码对应洛谷的树链剖分模板题。
首先,我们定义若干数组。
( exttt{fa[u]}):表示 (u) 点的父亲节点。
( exttt{siz[u]}):表示 (u) 点的子树大小。
( exttt{dep[u]}):表示 (u) 点的深度。
( exttt{wson[u]}):表示 (u) 点的重儿子。
( exttt{id[u]}):表示 (u) 点在 DFS 序中出现的位置。
( exttt{dfn[i]}):在 DFS 过程中第 (i) 个访问到的点。即 ( exttt{dfn}) 数组就是原树的 DFS 序。
( exttt{top[u]}):(u) 点所在重链的链头。
树链剖分中,我们需要做两次 DFS。第一次 DFS 求出每个点的父亲、深度、子树大小,并且根据儿子节点的子树大小确定重儿子。第二次 DFS 建立 DFS 序,形成若干条重链。
第一次 DFS 是比较基础的实现,对树的一些基本信息进行递归维护即可。
void dfs1(int u) {
siz[u] = 1;
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i];
if (v == fa[u]) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
dfs1(v);
siz[u] += siz[v];
// 根据定义更新重儿子。一开始 wson[u] 可以置为 0
if (siz[v] > siz[wson[u]]) wson[u] = v;
}
}
接下来的第二次 DFS 是树链剖分的核心。现在我们希望找出一种 DFS 的顺序,使得重链上的编号连续。由于每个非叶节点 (u) 有且仅有一个重儿子,因此我们递归到 (u) 时,可以优先递归到它的重儿子,这样这一条重链就会被连续地访问,自然就可以使得编号连续。
另外在 DFS 时,我们再传下去一个变量 ( exttt{chain}),表示当前重链的链头。
接下来是树剖第二次 DFS 的实现。我使用了一个变量 ( exttt{cntv}) 表示现在已经经过的节点数。
void dfs2(int u, int chain) {
cntv++;
id[u] = cntv; dfn[cntv] = u;
top[u] = chain;
// 如果不是叶子节点,则优先递归到重儿子
if (wson[u] != 0) dfs2(wson[u], chain);
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i];
if (v == fa[u] || v == wson[u]) continue;
// 从轻儿子开始再牵一条轻链
dfs2(v, v);
}
}
然后就转化成区间信息了,直接使用区间数据结构维护即可,注意维护的区间是 DFS 序。像这题就是使用线段树来维护。
至于路径修改和路径求和,假设我们已经已经写出来了线段树的区间加函数 ( exttt{Update_Tree(int l, int r, int val)}) 和线段树的区间求和函数 ( exttt{Query_Tree(int l, int r)}),那么现在我们要修改和查询一条路径 (u o v),我们可以把 (u), (v) 跳到同一条重链上,然后进行查询。我们可以写出如下的代码:
void Update_Path(int u, int v, int val) {
// 将 u, v 跳到同一条重链上
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
Update_Tree(id[top[u]], id[u], val);
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
Update_Tree(id[v], id[u], val);
}
int Query_Path(int u, int v) {
int res = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
res += Query_Tree(id[top[u]], id[u]);
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
res += Query_Tree(id[v], id[u]);
return res;
}
到这个时候,眼尖的读者可能会发现,( exttt{dfn}) 数组好像没什么用。。。实际上 ( exttt{dfn}) 数组是用来给线段树初始化时候用的,因为线段树维护的信息,就是这个 ( exttt{dfn}) 数组对应的信息。
给出本题的完整代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#define add(x, y) ((x + y) % Mod)
using namespace std;
typedef long long llt;
const int MaxN = 100000 + 5, MaxM = 200000 + 5;
const int MaxV = 400000 + 5;
int N, M, rt; int cntv, cnte;
llt Mod, A[MaxN];
int Head[MaxN], To[MaxM], Next[MaxM];
int fa[MaxN], siz[MaxN], dep[MaxN], wson[MaxN];
int id[MaxN], dfn[MaxN], top[MaxN];
struct SegTree {
int L[MaxV], R[MaxV];
llt sum[MaxV], tag[MaxV];
inline void push_up(int i) { sum[i] = add(sum[i << 1], sum[i << 1 | 1]); }
inline void push_down(int i) {
if (tag[i] != 0) {
int lson = i << 1, rson = i << 1 | 1;
tag[lson] = add(tag[lson], tag[i]);
tag[rson] = add(tag[rson], tag[i]);
sum[lson] = add(sum[lson], tag[i] * (R[lson] - L[lson] + 1));
sum[rson] = add(sum[rson], tag[i] * (R[rson] - L[rson] + 1));
tag[i] = 0;
}
}
void Build_Tree(int left, int right, int i) {
L[i] = left, R[i] = right;
if (L[i] == R[i]) {
sum[i] = A[dfn[left]];
return;
}
int mid = (L[i] + R[i]) >> 1;
Build_Tree(left, mid, i << 1);
Build_Tree(mid + 1, right, i << 1 | 1);
push_up(i);
}
void Update_Tree(int left, int right, llt val, int i) {
if (L[i] == left && R[i] == right) {
sum[i] = add(sum[i], val * (R[i] - L[i] + 1));
tag[i] = add(tag[i], val);
return;
}
push_down(i);
int mid = (L[i] + R[i]) >> 1;
if (right <= mid) Update_Tree(left, right, val, i << 1);
else if (left > mid) Update_Tree(left, right, val, i << 1 | 1);
else Update_Tree(left, mid, val, i << 1), Update_Tree(mid + 1, right, val, i << 1 | 1);
push_up(i);
}
llt Query_Tree(int left, int right, int i) {
if (L[i] == left && R[i] == right) return sum[i];
push_down(i);
int mid = (L[i] + R[i]) >> 1;
if (right <= mid) {
return Query_Tree(left, right, i << 1);
} else if (left > mid) {
return Query_Tree(left, right, i << 1 | 1);
} else {
llt lson = Query_Tree(left, mid, i << 1), rson = Query_Tree(mid + 1, right, i << 1 | 1);
return add(lson, rson);
}
}
} T;
inline void add_edge(int from, int to) {
cnte++; To[cnte] = to;
Next[cnte] = Head[from]; Head[from] = cnte;
}
void init() {
scanf("%d %d %d %lld", &N, &M, &rt, &Mod);
for (int i = 1; i <= N; ++i) scanf("%lld", &A[i]);
for (int i = 1; i < N; ++i) {
int u, v;
scanf("%d %d", &u, &v);
add_edge(u, v); add_edge(v, u);
}
}
void dfs1(int u) {
siz[u] = 1;
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i];
if (v == fa[u]) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
dfs1(v);
siz[u] += siz[v];
if (siz[v] > siz[wson[u]]) wson[u] = v;
}
}
void dfs2(int u, int chain) {
id[u] = ++cntv; dfn[cntv] = u;
top[u] = chain;
if (wson[u] != 0) dfs2(wson[u], chain);
for (int i = Head[u]; i; i = Next[i]) {
int v = To[i];
if (v == fa[u] || v == wson[u]) continue;
dfs2(v, v);
}
}
inline void Update_Subtree(int u, llt val) {
int l = id[u], r = id[u] + siz[u] - 1;
T.Update_Tree(l, r, val, 1);
}
inline llt Query_Subtree(int u) {
int l = id[u], r = id[u] + siz[u] - 1;
return T.Query_Tree(l, r, 1);
}
inline void Update_Path(int u, int v, llt val) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
T.Update_Tree(id[top[u]], id[u], val, 1);
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
T.Update_Tree(id[v], id[u], val, 1);
}
inline llt Query_Path(int u, int v) {
llt res = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
res = add(res, T.Query_Tree(id[top[u]], id[u], 1));
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
res = add(res, T.Query_Tree(id[v], id[u], 1));
return res;
}
void solve() {
dfs1(rt); dfs2(rt, rt);
T.Build_Tree(1, N, 1);
for (int i = 1; i <= M; ++i) {
int opt; scanf("%d", &opt);
if (opt == 1) {
int x, y; llt z;
scanf("%d %d %lld", &x, &y, &z);
Update_Path(x, y, z);
} else if (opt == 2) {
int x, y;
scanf("%d %d", &x, &y);
printf("%lld
", Query_Path(x, y));
} else if (opt == 3) {
int x; llt z;
scanf("%d %lld", &x, &z);
Update_Subtree(x, z);
} else {
int x; scanf("%d", &x);
printf("%lld
", Query_Subtree(x));
}
}
}
int main() {
init();
solve();
return 0;
}
上篇就更新完毕了…… 下篇我还会介绍一下点分治、动态 DP 和 LCT 这三种和树密切相关的算法。暂时就咕咕咕了