这里就算是一个小总结吧…
附参考的网址:
http://blog.sina.com.cn/s/blog_6a46cc3f0100s2qf.html
http://www.cnblogs.com/hankers/archive/2012/08/03/2622231.html
首先
Burnside引理:
Burnside引理:即互异状态个数等于各种转换下的等价类个数的和除以转换个数。
说人话: 按照这种 转法 转完了还是一样的个数除以转法数
举例:2*2的正方形 2种颜色染色 求不同的方案数
转法: 4种 0° 90° 270° 180°
0° 转完了 都一样吧.. (不就是不转嘛..) 2^4种
90° 和 270° 只有这两个转完了 一样
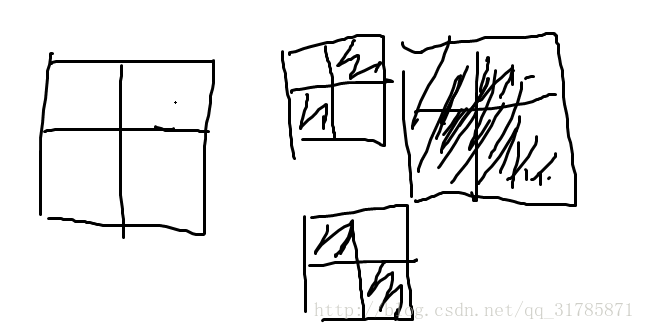
180° 4种 (如下图 图丑莫怪)
所以一共有 4种转法 和是16+2+2+4=24 本质不同的方案数 就是24/4=6个 大功告成
(证明看论文吧… 我叙述不清..http://www.docin.com/p-296856499.html)
蓝后 是 Polya
Polya就是Burnside的加强版 (不过适用性稍差 但是用起来极其方便)
Polya是这个样子的
说人话系列:
还拿2*2的方格说事吧..
我们已经知道了 有4种转法 分别是 0° 90° 270° 180°
循环个数 就是 你这几块 必须染同一个颜色
0° 不用说了吧 循环节 都是1 循环节个数 是4 所以方案数 是2^4=16
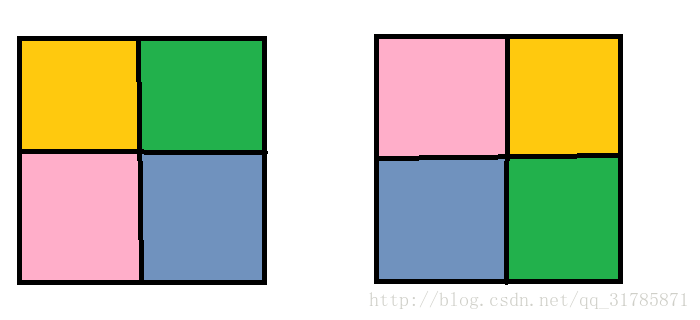
90°
这4块 都需要染一个颜色的 才能完全相同 所以循环节个数是1
2^1=2
270°同理
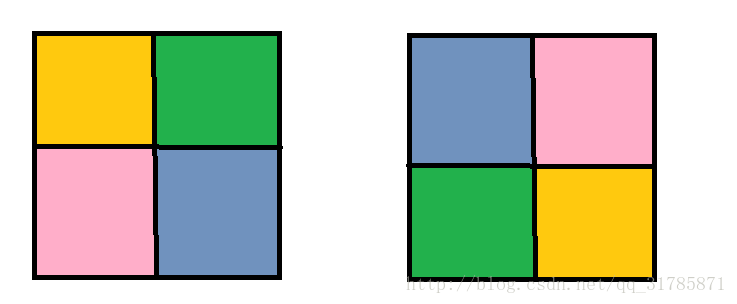
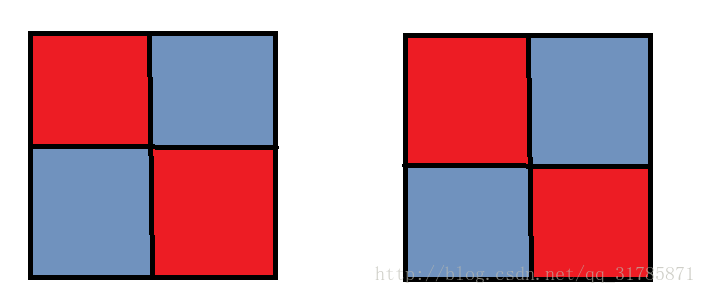
180°
诶 我们发现只要对角染同一个颜色即可
转完还是一样的
所以 循环节个数 是2 循环节大小 都是2 2^2=4
最后再这么一加 搞定~
光这么说 看起来 很麻烦 还不如直接一个一个数呢
那我来出(copy)一道题
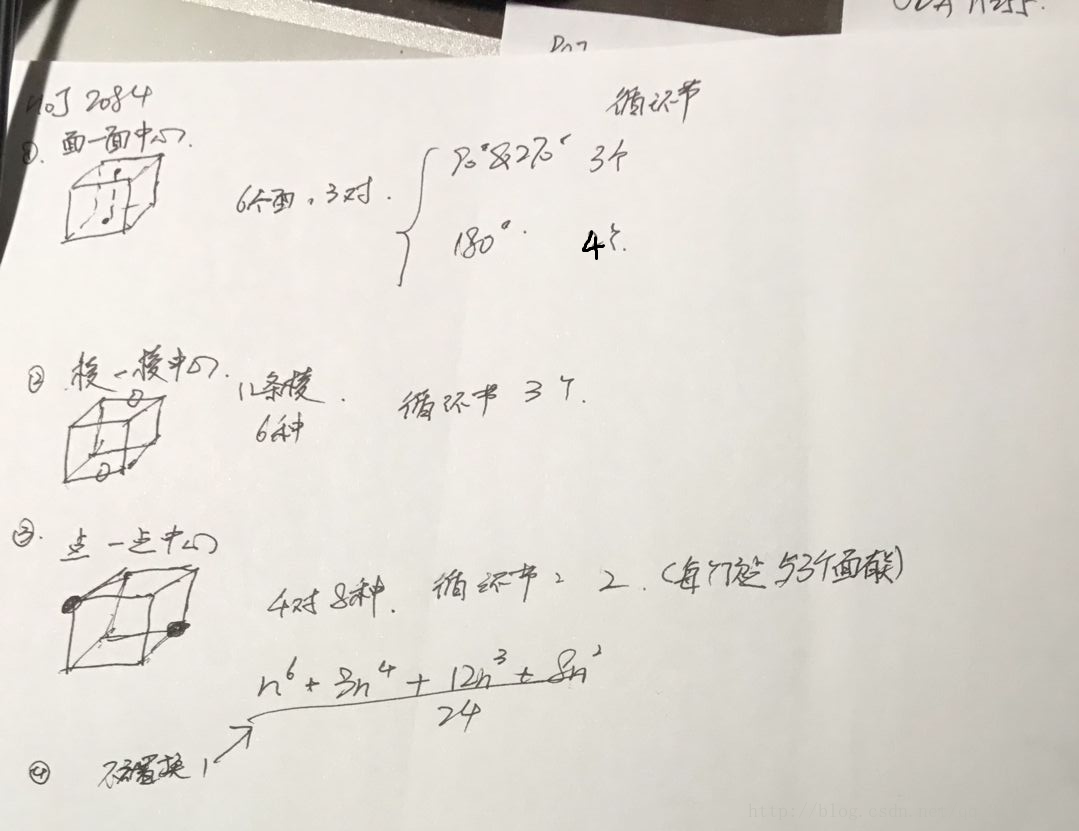
HOJ 2084 The Colored Cubes
http://acm.hit.edu.cn/hoj/problem/view?id=2084
题意:用n种颜色为正六面体染色,求有多少种不同的情况。
思路:
我写得可能不太详细,,,详细解释一下..
首先 面-面中心 90 180 270 三种情况
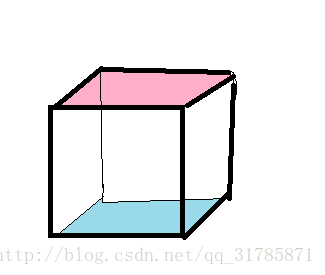
90 &270的时候 是
这个样子的 上面 和 底下 循环节长度为1 中间必须染同样的颜色 循环节长度为4
所以一共是三个循环节
180度 的时候 是 前后一样 左右一样 上 下 可以不同 所以 是4个循环节 长度分别为2,2,2,2
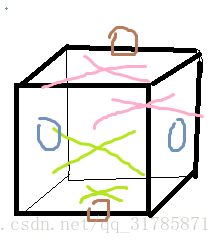
棱 棱 中心 是这个样子的
假设 是两个用咖啡色标成的棱为中心 上 和后一样 前和下一样 左和右一样
三个循环 循环节长度都是2
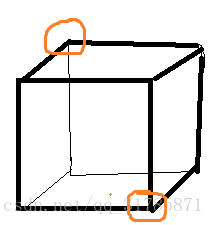
最后 是点-点中心
与顶点相邻的三个边 必须要染成一样的颜色 所以 循环节个数是2 循环节长度是3
(注意有两种循环的方式 120和 240)所以点点中心的总方案数是4*2=8种
再加上不动置换 除一下总 转法就好啦~
Code 大概长这样…
//By SirisuRen
#include <cstdio>
using namespace std;
long long n;
int main(){
while(scanf("%lld",&n)&&n)
printf("%lld
",(n*n*n*n*n*n+3*n*n*n*n+12*n*n*n+8*n*n)/24);
}现在知道Polya的奇妙了吧。。
(某小明同学不服 他暴搜+打表找到了规律)
再来个这个
HOJ 2647 给12面体 染色
小明同学晕倒
但是我不怂啊
还是按照上题一样分析
我们观察得 每个面都是五边形
1. 面面 上下两个面 可以不同 与上下两个面相接的那两层可以不同
所以 循环节有4个 可以转 72° 144° 216° 288° 所以有6*4种转的方法
2. 棱棱 通过一通乱数 可以得到循环节有6个 (我实在不知道怎么描述了) 15种
3. 点点 循环节有4个 20种
4. 不动置换
代码很简单…
是这样子的..
//By SirisuRen
#include <cstdio>
using namespace std;
long long n;
int main(){
while(~scanf("%lld",&n))
printf("%lld
",(n*n*n*n*n*n*n*n*n*n*n*n+15*n*n*n*n*n*n+44*n*n*n*n)/60);
}上面的都还是小case (考试才不可能考这玩意呢)
POJ 2409
//By SiriusRen
#include <cstdio>
using namespace std;
int n,m;
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int pow(int x,int y){
int res=x,ans=1;
while(y){
if(y&1)ans=ans*res;
res=res*res;
y>>=1;
}return ans;
}
int main(){
while(scanf("%d%d",&n,&m)&&(n||m)){
int ans=0;
for(int i=1;i<=m;i++)ans+=pow(n,gcd(i,m));
if(m&1)ans+=m*pow(n,m/2+1);
else ans+=m/2*(pow(n,m/2+1)+pow(n,m/2));
ans/=2*m;
printf("%d
",ans);
}
}POJ 1286
//By SiriusRen
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
int n;
typedef long long ll;
int main(){
while(~scanf("%d",&n)&&n>=0){
if(n==0){puts("0");continue;}
ll ans=0;
for(int i=1;i<=n;i++)ans+=pow(3,__gcd(i,n));
if(n&1)ans+=n*pow(3,n/2+1);
else ans+=n/2*(pow(3,n/2+1)+pow(3,n/2));
printf("%lld
",ans/2/n);
}
}Hdu1812 懒得写高精了.. 用long long 测了几个小数据对了(就不放程序了)
TJU 2795 http://acm.tju.edu.cn/toj/showp2795.html 又要高精
对于高精我是拒绝的 就没写
UVA 11255 long long 可以水的..# Problem Verdict Language Run Time Submission Date
18804966 11255 Necklace Accepted C++ 0.000 2017-02-19 10:15:34
(UVA怎么看自己交的代码啊啊啊 算了我放一份题解吧)
http://blog.csdn.net/overload1997/article/details/53055361
POJ 2154
//By SiriusRen
#include <cstdio>
using namespace std;
bool vis[35050];
int pri[35050],phi[35050],tot,n,p,cases;
void getphi(){
phi[1]=1;
for(int i=2;i<=35000;i++){
if(!vis[i])pri[++tot]=i,phi[i]=i-1;
for(int j=1;j<=tot&&i*pri[j]<=35000;j++){
vis[i*pri[j]]=1,phi[i*pri[j]]=phi[i]*(pri[j]-1);
if(i%pri[j]==0){phi[i*pri[j]]=phi[i]*pri[j];break;}
}
}
}
int pow(int x,int y){
int ans=1,res=x%p;
while(y){
if(y&1)ans=ans*res%p;
res=res*res%p;
y>>=1;
}return ans;
}
int Phi(int x){
if(x<35000)return phi[x]%p;
int res=x;
for(int i=1;i<=tot&&pri[i]*pri[i]<=x;i++)
if(!(x%pri[i])){
res-=res/pri[i];
while(x%pri[i]==0)x=x/pri[i];
}
if(x>1)res-=res/x;
return res%p;
}
int main(){
getphi();
scanf("%d",&cases);
while(cases--){
scanf("%d%d",&n,&p);
int ans=0;
for(int i=1;i*i<=n;i++)if(!(n%i)){
if(i*i==n){ans=(ans+Phi(i)*pow(n,i-1))%p;break;}
ans=(ans+Phi(n/i)*pow(n,i-1)+pow(n,n/i-1)*Phi(i))%p;
}
printf("%d
",ans);
}
}POJ 2888
(有秦神的题解 冰封寒月 sina)woc高一9月份写这题…OTZ
//By SiriusRen
#include <cstdio>
#include <cstring>
using namespace std;
int cases,n,m,k,mod=9973,phi[35005],p[35005],vis[35005],tot,xx,yy,ans;
struct Matrix{int a[11][11];void init(){memset(a,0,sizeof(a));}}fst;
Matrix operator*(Matrix a,Matrix b){
Matrix c;c.init();
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++){
for(int k=1;k<=m;k++)
c.a[i][j]+=a.a[i][k]*b.a[k][j];
c.a[i][j]%=mod;
}
return c;
}
Matrix pow(Matrix a,int b){
Matrix c;c.init();
for(int i=1;i<=m;i++)c.a[i][i]=1;
while(b){
if(b&1)c=c*a;
a=a*a;
b>>=1;
}return c;
}
void getphi(){
phi[1]=1;
for(int i=2;i<=35000;i++){
if(!vis[i])p[++tot]=i,phi[i]=i-1;
for(int j=1;j<=tot&&i*p[j]<=35000;j++){
vis[i*p[j]]=1,phi[i*p[j]]=phi[i]*(p[j]-1);
if(!(i%p[j])){phi[i*p[j]]=phi[i]*p[j];break;}
}
}
}
int Phi(int x){
if(x<=35000)return phi[x]%mod;
int res=x;
for(int i=1;i<=tot&&p[i]*p[i]<=x;i++){
if(!(x%p[i])){
res-=res/p[i];
while(!(x%p[i]))x/=p[i];
}
}
if(x>1)res-=res/x;
return res%mod;
}
int calc(int x){
Matrix tmp=pow(fst,x);
int temp=0;
for(int i=1;i<=m;i++)temp+=tmp.a[i][i];
return temp%mod;
}
int pow(int x,int y){
int tmp=1;x%=mod;
while(y){
if(y&1)tmp=tmp*x%mod;
x=x*x%mod;
y>>=1;
}return tmp;
}
int main(){
scanf("%d",&cases);
getphi();
while(cases--){
scanf("%d%d%d",&n,&m,&k),ans=0;
for(int i=1;i<=m;i++)for(int j=1;j<=m;j++)fst.a[i][j]=1;
for(int i=1;i<=k;i++){
scanf("%d%d",&xx,&yy);
fst.a[xx][yy]=fst.a[yy][xx]=0;
}
for(int i=1;i*i<=n;i++){
if(i*i==n)ans=(ans+calc(i)*phi[i])%mod;
if(!(n%i))ans=(ans+calc(i)*Phi(n/i)+calc(n/i)*phi[i])%mod;
}
printf("%d
",ans*pow(n,mod-2)%mod);
}
}TJU 3352
嘴巴AC一下
首先 n 和k 都很大 10^9的 线性肯定是不行滴
先想线性怎么做
dp[i]表示循环节长度为i有多少种方案
dp[i]=k*(k-1)^(i-1)-dp[i-1];
诶? woc ? 可以矩阵乘法优化
构造一个转移矩阵
dp[i] 常数
-1 0
1 k-1
2*2的
嘿嘿 然后就无聊了 搞个phi 筛一筛 算一算 判一判 嘴巴搞定~