leetcode刷题

好好刷题

反转整数(easy)

$ 2^ {31} -1=2147483647 $

$ -2^{31} =-2147483648 $

数学方法

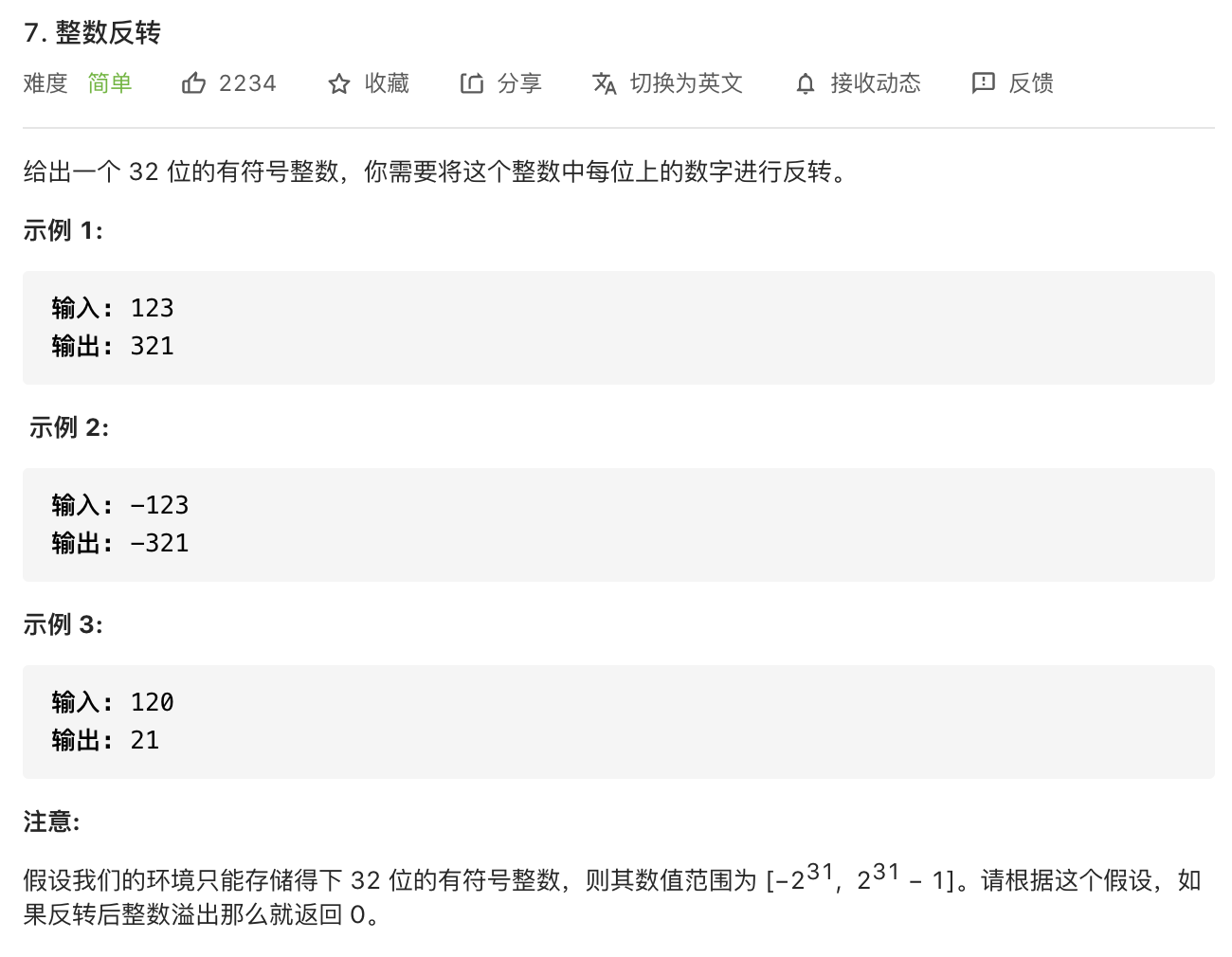
一般做法：取模运算

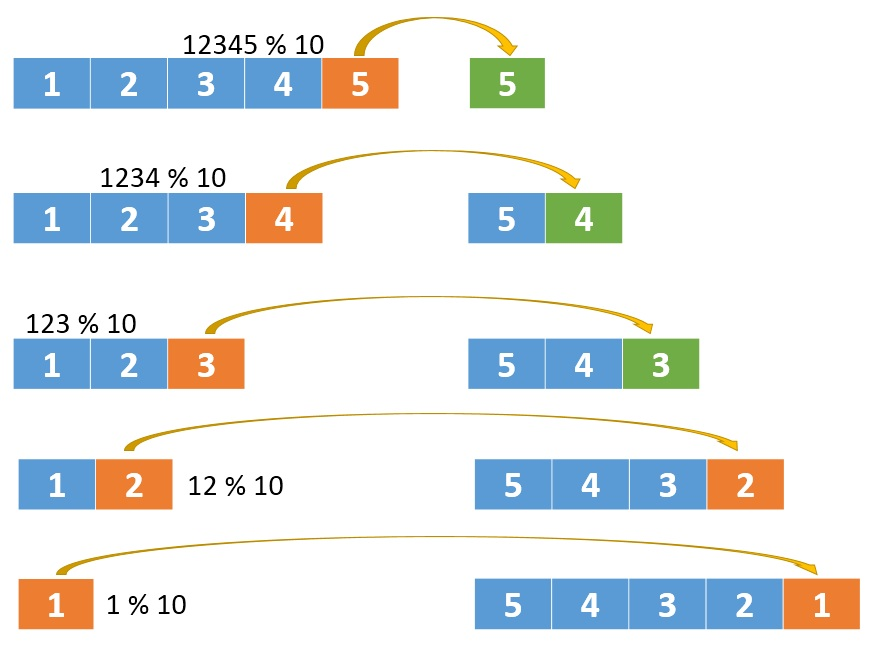
但是忽略了负数以及题目范围

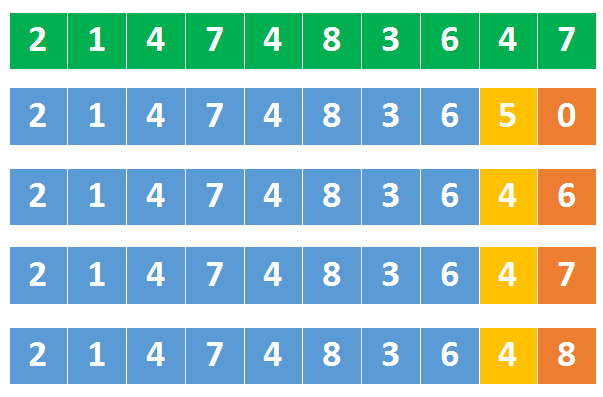
上图中，绿色的是最大32位整数
第二排数字中，橘子的是5，它是大于上面同位置的4，这就意味着5后跟任何数字，都会比最大32为整数都大。
所以，我们到【最大数的1/10】时，就要开始判断了
如果某个数字大于 214748364那后面就不用再判断了，肯定溢出了。
如果某个数字等于 214748364呢，这对应到上图中第三、第四、第五排的数字，需要要跟最大数的末尾数字比较，如果这个数字比7还大，说明溢出了。

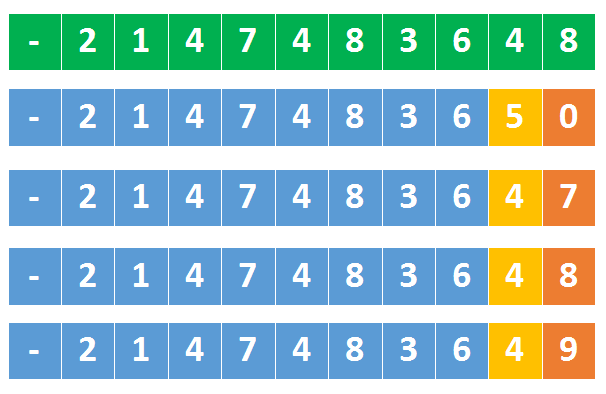
负数同理

class Solution {
    public int reverse(int x) {
        int res = 0;
        while(x!=0) {
            //每次取末尾数字
            int tmp = x%10;
            //判断是否 大于 最大32位整数
            if (res>214748364 || (res==214748364 && tmp>7)) {
                return 0;
            }
            //判断是否 小于 最小32位整数
            if (res<-214748364 || (res==-214748364 && tmp<-8)) {
                return 0;
            }
            res = res*10 + tmp;
            x /= 10;
        }
        return res;
    }
}			

关键点：
1.判断整数的正负
2.判断反转后的整数是否溢出

切片反转

python的话可以直接转成字符串切片

class Solution:
    def reverse(self, x: int) -> int:
        #将整数的绝对值转换成字符串
        s=str(abs(x))
        #翻转字符串
        s=s[::-1]
        #如果输入整数是负数，增加负号
        if x <0:
            s ='-' + s
        #转换为整数
        result = int(s)
        #判断是否溢出
        if result>=-2**31 and result<=2**31-1:
            return result
        else:
            return 0

还有大佬写的很丝滑

class Solution:
    def reverse(self, x: int) -> int:
        s = str(x)
        if s[0] == '-':
            x = int('-' + s[1:][::-1])
        else:
            x = int(s[::-1])
        return x if -2147483648< x <2147483647 else 0

我们可以一次构建反转整数的一位数字。在这样做的时候，我们可以预先检查向原整数附加另一位数字是否会导致溢出。
反转整数的方法可以与反转字符串进行类比。

我们想重复 “弹出” x 的最后一位数字，并将它 “推入” 到 res 的后面。最后，res 将与 x 相反。

取模

def reverse_better(self, x: int) -> int:
        y, res = abs(x), 0
        # 则其数值范围为 [−2^31,  2^31 − 1]
        boundry = (1<<31) -1 if x>0 else 1<<31
        while y != 0:
            res = res*10 +y%10
            if res > boundry :
                return 0
            y //=10
        return res if x >0 else -res

这里用移位来表示的边界$ 1<<31=2^{31} $
先将x进行abs，取绝对值，所以当x小于零的话边界就是1<<31，如果大于零就是(1<<31) -1，数字y>boundry就表示数字在范围外，这里的数字y其实就是x的取绝对值的数，所以可以这样表示，return的时候再把负号加上去

复习一下 python 的位运算符：

(a & b)
按位与运算符：参与运算的两个值，如果两个相应位都为 1，则该位的结果为 1，否则为 0 。
输出结果 12 ，二进制解释： 0000 1100

(a | b)
按位或运算符：只要对应的二个二进位有一个为1时，结果位就为1。
输出结果 61 ，二进制解释： 0011 1101

(a ^ b)
按位异或运算符：当两对应的二进位相异时，结果为 1
输出结果 49 ，二进制解释： 0011 0001

(~a )
按位取反运算符：对数据的每个二进制位取反，即把 1 变为 0，把 0 变为 1 。~x 类似于 -x-1
输出结果 -61 ，二进制解释： 1100 0011，在一个有符号二进制数的补码形式。

a << 2
左移动运算符：运算数的各二进位全部左移若干位，由 << 右边的数字指定了移动的位数，高位丢弃，低位补 0。
输出结果 240 ，二进制解释： 1111 0000

a >> 2
右移动运算符：把 ">>" 左边的运算数的各二进位全部右移若干位，>> 右边的数字指定了移动的位数
输出结果 15 ，二进制解释： 0000 1111

python 赋值运算符：

*= 乘法赋值运算符 c *= a 等效于 c = c * a
/= 除法赋值运算符 c /= a 等效于 c = c / a
%= 取模赋值运算符c %= a等效于 c = c % a
**= 幂赋值运算符 c **= a 等效于 c = c ** a
//= 取整除赋值运算符 c //= a 等效于 c = c // a

栈思路

class Solution:
    def reverse(self, x: int) -> int:
        stack = []              # 创建一个中间栈
        x = str(x)
        for i in x:
            if i != 0:          # 消除0 将已转换的字符串压入栈
                stack.append(i)
        if stack[0] == '-':     # 负号情况下 栈底为-号 将其删掉 补到栈顶
            stack.pop(0)
            stack.append('-')
        s = int(''.join(stack[::-1])) # 栈反转正好是反转的数字

        if s >= 2147483647 or s <= -2147483648: # 判断溢出情况
            return 0
        return s

罗马数字转整数(easy)

分析题目，只有在遇到特殊情况时，两个字符中左边的字符小于右边的字符，且等于右边的字符代表的数减左边字符代表的数。 比如 CM 等于 1000 - 1001000−100，XC 等于 100 - 10100−10...

其他情况就直接加就行了

那么我们只需要读取输入 遍历hashmap 判断是否需要减 就可以了

class Solution:
    def romanToInt(self, s: str) -> int:
        m = {'I':1, 'V':5, 'X':10, 'L':50, 'C':100, 'D':500, 'M':1000}
        result = 0

        for i in range(len(s)):
            if i < len(s)-1 and m[s[i]] < m[s[i+1]]:
                result -= m[s[i]]
            else:
                result += m[s[i]]

        return result

最长公共前缀

python两种让你拍大腿的解法，时间复杂度你想象不到，短小精悍。
1、利用python的max()和min()，在Python里字符串是可以比较的，按照ascII值排，举例abb， aba，abac，最大为abb，最小为aba。所以只需要比较最大最小的公共前缀就是整个数组的公共前缀

def longestCommonPrefix(self, strs):
   if not strs: return ""
   s1 = min(strs)
   s2 = max(strs)
   for i,x in enumerate(s1):
       if x != s2[i]:
           return s2[:i]
   return s1

2、利用python的zip函数，把str看成list然后把输入看成二维数组，左对齐纵向压缩，然后把每项利用集合去重，之后遍历list中找到元素长度大于1之前的就是公共前缀

def longestCommonPrefix(self, strs):
   if not strs: return ""
   ss = list(map(set, zip(*strs)))
   res = ""
   for i, x in enumerate(ss):
       x = list(x)
       if len(x) > 1:
           break
       res = res + x[0]
   return res