HDU

题意：在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的： 有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？ 

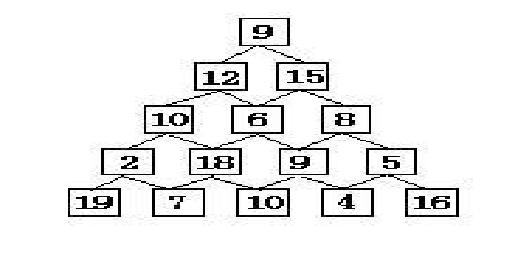
分析：按照行走路径状态转移即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define lowbit(x) (x & (-x))
const double eps = 1e-8;
inline int dcmp(double a, double b){
    if(fabs(a - b) < eps) return 0;
    return a > b ? 1 : -1;
}
typedef long long LL;
typedef unsigned long long ULL;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const LL LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {0, 0, -1, 1, -1, -1, 1, 1};
const int dc[] = {-1, 1, 0, 0, -1, 1, -1, 1};
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
const int MAXN = 100 + 10;
const int MAXT = 250000 + 10;
using namespace std;
int a[MAXN][MAXN];
int dp[MAXN][MAXN];
int main(){
    int T;
    scanf("%d", &T);
    while(T--){
        memset(dp, 0, sizeof dp);
        int N;
        scanf("%d", &N);
        for(int i = 1; i <= N; ++i){
            for(int j = 1; j <= i; ++j){
                scanf("%d", &a[i][j]);
            }
        }
        dp[1][1] = a[1][1];
        for(int i = 2; i <= N; ++i){
            for(int j = 1; j <= i; ++j){
                if(j == 1){
                    dp[i][j] = max(dp[i][j], dp[i - 1][j] + a[i][j]);
                }
                else if(j == i){
                    dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + a[i][j]);
                }
                else{
                    dp[i][j] = max(dp[i - 1][j - 1] + a[i][j], dp[i - 1][j] + a[i][j]);
                }
            }
        }
        int ans = 0;
        for(int i = 1; i <= N; ++i){
            ans = max(ans, dp[N][i]);
        }
        printf("%d
", ans);
    }
    return 0;
}