Matrix_tree Theorem 矩阵树定理学习笔记

Matrix_tree Theorem:

给定一个无向图, 定义矩阵A

A[i][j] = - (<i, j>之间的边数)

A[i][i] = 点i的度数

其生成树的个数等于 A的任意n - 1阶主子式的值。

关于定理的相关证明 可以看这篇文章, 讲得非常详细, 耐心看就能看懂：

 

 

关于求行列式, 可以用高斯消元。 如果是模域下求行列式, 可以用欧几里得算法。 具体实现看这篇文章

模域下求行列式 模板题：SPOJ DETER3

代码：

#include <cstdio>
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <set>
#include <cmath>
using namespace std;

#define N 220
#define M 400010
typedef long long ll;

const int Mod=1000000007;
const double eps = 1e-9;

ll Solve(ll a[N][N], int n, ll mod)
{
    ll res = 1;
    for (int i = 1; i <= n; ++i)
    {
        for (int j = i; j <= n; ++j)
        {
            if (a[j][i] < 0)
            {
                res *= -1;
                for (int k = i; k <= n; ++k)
                    a[j][k] *= -1;
            }
        }
        int j;
        for (j = i; j <= n && !a[j][i]; ++j);
        if (j > n) return 0;
        
        if (j != i)    
        {
            res = -res;
            for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
        }
        
        for (j = i + 1; j <= n; ++j)
        {
            while (a[j][i])
            {
                ll d = a[i][i] / a[j][i];
                for (int k = i; k <= n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
                for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
                res = -res;
            }
        }
        res = res * a[i][i] % mod;
    }
    if (res < 0) res += mod;
    return res;
}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    int n; ll mod; 
    while (scanf("%d %lld", &n, &mod) != EOF)
    {
        ll a[N][N];
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= n; ++j)
                scanf("%lld", &a[i][j]);
        printf("%lld
", Solve(a, n, mod));
    }
    
    return 0;
}

 

 

下面给出一些应用(练习题):

 

应用一：SPOJ HIGH

模板题： 给出一个无向图, 求生成树个数。

代码：

#include <cstdio>
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <set>
#include <cmath>
using namespace std;

#define N 13
#define M 400010
typedef long long ll;

const int Mod=1000000007;
const double eps = 1e-9;

double Solve(int n, double a[N][N])
{
    if (n == 0) return 1;
    
    /*for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            printf("%.0lf%c", a[i][j], j == n? '
':' ');*/
    
    double res = 1;
    for (int i = 1; i <= n; ++i)
    {
        int j;
        for (j = i; j <= n && fabs(a[j][i]) < eps; ++j);
        if (j > n) return 0;
        if (j != i) for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
        
        for (int j = i + 1; j <= n; ++j)
        {
            double f = a[j][i] / a[i][i];
            for (int k = i; k <= n; ++k)
                a[j][k] -= f * a[i][k];
        }
        res *= a[i][i];
    }

    return res;
}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    int T, n, m, x, y;
    scanf("%d", &T);
    while (T--)
    {
        double a[N][N] = {0};
        scanf("%d %d", &n, &m);
        for (int i = 1; i <= m; ++i)
        {
            scanf("%d %d", &x, &y);
            a[x][y]--, a[y][x]--;
            a[x][x]++, a[y][y]++;
        }
        printf("%.0lf
", Solve(n - 1, a));
    }
    
    return 0;
}

 

---

 

 

应用二：BZOJ 4031

构图后 求生成树个数 mod 一个数。

#include <cstdio>
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <set>
#include <cmath>
using namespace std;
 
#define N 120
#define M 400010
typedef long long ll;
 
const int Mod=1000000007;
const double eps = 1e-9;
 
ll Solve(ll a[N][N], int n, ll mod)
{
    if (n == 0) return 1;
    ll res = 1;
    for (int i = 1; i <= n; ++i)
    {
        //for (int p = 1; p <= n; ++p)
        //  for (int q = 1; q <= n; ++q)
        //      printf("%lld%c", a[p][q], q == n? '
':' ');
         
        for (int j = i; j <= n; ++j) 
        {
            if (a[j][i] < 0)
            {
                res = -res;
                for (int k = i; k <= n; ++k) a[j][k] *= -1;
            }
        }   
         
        int j;
        for (j = i; j <= n && !a[j][i]; ++j);
        if (j > n) return 0;
         
        if (j != i)
        {
            res = -res;
            for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
        }
         
         
        for (j = i + 1; j <= n; ++j)
        {
            while (a[j][i])
            {
                ll d = a[i][i] / a[j][i];
                for (int k = i; k <= n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
                res = -res;
                for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
            }
        }
        res = res * a[i][i] % mod;
    //  printf("res = %lld
", res);
    }
    if (res < 0) res += mod;
//  cout << "aa= "<<res <<endl;
    return res;
}
 
int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
     
    int n, m; ll mod = 1000000000; 
    char mp[11][11]; int tot = 0;
    int id[11][11];
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            scanf(" %c", &mp[i][j]);
            if (mp[i][j] == '.') id[i][j] = ++tot;
        }
    }
    ll a[N][N] = {0};
    for (int i = 1; i < n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            if (mp[i][j] == '.' && mp[i + 1][j] == '.')
            {
                int x = id[i][j], y = id[i + 1][j];
                a[x][y]--, a[y][x]--;
                a[x][x]++, a[y][y]++;
            }
        }
    }
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j < m; ++j)
        {
            if (mp[i][j] == '.' && mp[i][j + 1] == '.')
            {
                int x = id[i][j], y = id[i][j + 1];
                a[x][y]--, a[y][x]--;
                a[x][x]++, a[y][y]++;
            }
        }
    }
    printf("%lld
", Solve(a, tot - 1, mod));
    return 0;
}

 

---

 

应用三： BZOJ 2467

这题数据范围比较小,可以暴力建图 然后跑Matrix tree。

另外可以直接推公式：

一共有4n个点, 5n条边, 所以要删去n - 1条边, 然后可以发现 每个五边形外面的4条边最多只能删一条。

根据鸽笼原理合法的解 一定是 有一个五边形删去了里面的那条边 和外面的某条边, 其余的五边形删去了任意一条边。

所以答案就是$4*n*5^{n-1}$

Matrix tree 代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
using namespace std;
 
#define X first
#define Y second
#define N 420
#define M 11
 
typedef long long ll;
const int Mod = 1000000007;
const int INF = 1 << 30;
 
void Add(int x, int y, int &tot, int a[N][N])
{
    a[x][tot + 1] = a[tot + 1][x] = -1;
    a[tot + 1][tot + 2] = a[tot + 2][tot + 1] = -1;
    a[tot + 2][tot + 3] = a[tot + 3][tot + 2] = -1;
    a[tot + 3][y] = a[y][tot + 3] = -1;
    a[tot + 1][tot + 1] = a[tot + 2][tot + 2] = a[tot + 3][tot + 3] = 2;
    a[x][x] = a[y][y] = 4; tot += 3;
    a[x][y]--,a[y][x]--;
}
 
int Solve(int n, int a[N][N], int mod)
{
 
    if (n == 0) return 1;
    int res = 1;
    for (int i = 1; i <= n; ++i)
    {
        for (int j = i; j <= n; ++j)
        {
            if (a[j][i] < 0)
            {
                res = -res;
                for (int k = i; k <= n; ++k) a[j][k] = -a[j][k];
            }
        }
        //cout << i << endl;
        //for (int p = 1; p <= n; ++p)
        //  for (int q = 1; q <= n; ++q)
        //  printf("%d%c", a[p][q], q == n? '
':' ');
        //printf("
");
        int j;
        for (j = i; j <= n && !a[j][i]; ++j);
        if (j > n) return 0;
        if (i != j)
        {
            res = -res;
            for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
        }
         
        for (j = i + 1; j <= n; ++j)
        {
            while (a[j][i])
            {
                int d = a[i][i] / a[j][i];
                for (int k = i; k <= n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
                res = -res;
                for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
            }
        }
        res = res * a[i][i] % mod;
    }
    if (res < 0) res += mod;
    return res;
}
 
int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
     
    int T; scanf("%d", &T);
    while (T--)
    {
        int n, mod = 2007, tot, a[N][N] = {0}; scanf("%d", &n); tot = n;
        for (int i = 1; i < n; ++i) Add(i, i + 1, tot, a);
        Add(n, 1, tot, a); 
        printf("%d
", Solve(tot - 1, a, mod));
    }
    return 0;
}

 

---

 

 

应用四：BZOJ 1016 

题目大意：求最小生成树个数。

性质一：无向图所有MST中，相同权值的边数一样多。

证明看https://blog.sengxian.com/solutions/bzoj-1016

性质二：对于任意MST，加入所有权值<=w的边后, 形成的森林连通性相同 。

证明：

考虑Kruskal算法的过程，我们首先会尽可能多的加入权值最小的边。这个过程相当于拿出所有权值最小的边，然后任意求一颗生成树，因此我们可以知道，能加入的权值最小的边的数量是一定的，而且加入这些边之后 形成的森林连通性相同。 

结合性质一，对于任意一棵MST，因为它包含的权值最小的边数和做Kruskal算法求出的MST包含的边数是一样的，这些边又不能形成环，因此这些边形成的森林和 做Kruskal时形成的森林连通性是一样的。  对于任意MST，加入所有权值最小的边后, 形成的森林连通性相同 。

然后我们考虑把已经形成的联通块缩点， 考虑所有权值第二小的边，重复上面的过程，可以证明对于任意MST，加入所有权值<=w的边后, 形成的森林连通性相同 。

 

所以我们的算法就可以模拟这个过程, 把边按权值从小到大排好序, 每次加入权值相同的所有边, 形成一些连通块， 然后对于每个连通块, 跑Matrix tree 求出形成这个连通块有多少种方案。      统计好之后每个连通块缩点,  进行下一种权值的边的加边操作。       代码实现起来还是挺多细节的。

 

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
using namespace std;

#define X first
#define Y second
#define N 120
#define M 1010

typedef long long ll;
const int Mod = 1000000007;
const int INF = 1 << 30;

struct Edge
{
    int x, y, z;
    bool operator < (const Edge &t)const{return z < t.z;}
}e[M];


int Solve(int n, int a[N][N], int mod)
{
    if (n == 0) return 1;
    int res = 1;
    for (int i = 0; i < n; ++i)
    {
        for (int j = i; j < n; ++j)
        {
            if (a[j][i] < 0)
            {
                res = -res;
                for (int k = i; k < n; ++k) a[j][k] = -a[j][k];
            }
        }
        int j;
        for (j = i; j < n && !a[j][i]; ++j);
        if (j == n) return 0;
        if (i != j)
        {
            res = -res;
            for (int k = i; k < n; ++k) swap(a[i][k], a[j][k]);
        }
        
        for (j = i + 1; j < n; ++j)
        {
            while (a[j][i])
            {
                int d = a[i][i] / a[j][i];
                for (int k = i; k < n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
                res = -res;
                for (int k = i; k < n; ++k) swap(a[i][k], a[j][k]);
            }
        }
        res = res * a[i][i] % mod;
    }
    if (res < 0) res += mod;
    return res;
}


int father[N], id[N], pa[N], num[N];
vector<int> lis[N];
vector<pair<int, int> > ed[N];

int Find(int x)
{
    if (father[x] == x) return x;
    father[x] = Find(father[x]);
    return father[x];
}

void Merge(int x, int y)
{
    x = Find(x), y = Find(y);
    if (x != y) father[x] = y;
}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    int n, m, mod = 31011; 
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= m; ++i) scanf("%d %d %d", &e[i].x, &e[i].y, &e[i].z);
    sort(e + 1, e + m + 1);
    
    int res = 1, block = n;
    for (int i = 1; i <= n; ++i) id[i] = i;
    for (int l = 1, r; l <= m;)
    {
        for (r = l; r < m && e[r + 1].z == e[l].z; ++r);
        for (int i = 1; i <= block; ++i) father[i] = i;
        for (r = l; r < m && e[r + 1].z == e[l].z; ++r);
        for (int i = l; i <= r; ++i) Merge(id[e[i].x], id[e[i].y]);
        
        int tot = 0;
        for (int i = 1; i <= block; ++i) if (father[i] == i) pa[i] = ++tot;
        for (int i = 1; i <= block; ++i) pa[i] = pa[Find(i)];
        for (int i = 1; i <= block; ++i) lis[pa[i]].push_back(i), num[i] = lis[pa[i]].size() - 1;
        for (int i = l; i <= r; ++i)
        {
            int x = id[e[i].x], y = id[e[i].y];
            if (x == y) continue;
            ed[pa[x]].push_back(make_pair(num[x], num[y]));
        }
        for (int i = 1; i <= tot; ++i)
        {
            int a[N][N] = {0}, x, y;
            for (int j = 0; j < ed[i].size(); ++j)
            {
                x = ed[i][j].X, y = ed[i][j].Y;
                a[x][x]++, a[y][y]++;
                a[x][y]--, a[y][x]--;
            }
            res = res * Solve(lis[i].size() - 1, a, mod) % mod;
        }
        
        for (int i = 1; i <= n; ++i) id[i] = pa[id[i]];
        for (int i = 1; i <= tot; ++i) lis[i].clear(), ed[i].clear();
        block = tot;  l = r + 1;
    }
    if (block > 1) puts("0");
    else printf("%d
", res);
    return 0;
}

 

---

 

 

应用五：  BZOJ 3534   Matrix Tree Theorem 的扩展, 非常精彩的题。

题目大意：

给出一个无向图, 两点之间的连边会有一个概率， 求连成一颗树的概率。

 

这个题如果没有看过Matrix Tree Theorem定理的证明,只是记住结论 应该是做不出来的。。。

 

先来看一个简化版本：

给出一个无向图, 定义它的一棵生成树的权值为所有边权的乘积。 求所有生成树的权值和。 ( 原题还要考虑一些边不选的概率 这题只靠考虑选的边）

 

参考最前面给出的 证明Matrix Tree Theorem定理的文章。

原来是

A[i][j] = - (<i, j>之间的边数)

A[i][i] = 点i的度数

 

现在改成

A[i][j] = - (<i, j>之间的所有边权和)

A[i][i] = 和i相连的所有边的边权和

 

修改关联矩阵B的定义, 把1 改成 $e_j$的边权开根号后的值。

 

 

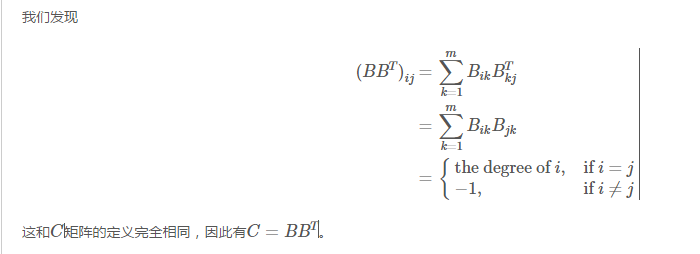
 这里也做相应的修改, 把 -1 改成 -<i,j>之间的边权和, the degree of i 改成和i相连的所有边的边权和。

 

 

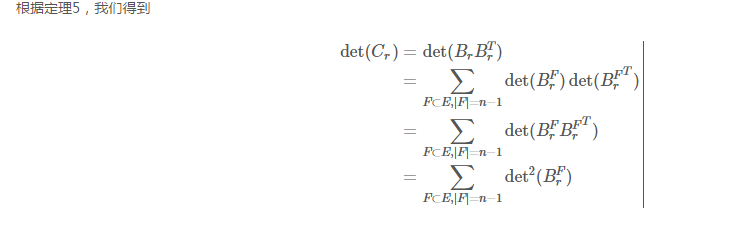
 做了以上修改之后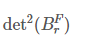刚好就是所选的生成树的边权的乘积。

所以用修改后的A数组跑Matrix Tree就可以解决这个问题了。

当然原题 还要乘上 其他边不选的概率。  再对A数组做点小修改就好了。具体实现看代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
using namespace std;
 
#define X first
#define Y second
#define N 100
#define M 11
 
typedef long long ll;
const int Mod=1000000007;
const int INF=1<<30;
 
const double eps = 1e-10;
 
double Solve(double a[N][N], int n)
{
    if (n == 0) return 1;
    double res = 1;
    for (int i = 1; i <= n; ++i)
    {
        int j = i;
        for (int k = i + 1; k <= n ; ++k) if (fabs(a[k][i]) > fabs(a[j][i])) j = k;
        if (fabs(a[j][i]) < eps) return 0;
        if (i != j)
        {
            res = -res;
            for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
        }
         
        for (j = i + 1; j <= n; ++j)
        {
            double f = a[j][i] / a[i][i];
            for (int k = i; k <= n; ++k) a[j][k] -= f * a[i][k];
        }
        res *= a[i][i];
    }
    return res;
}
 
int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
     
    int n; 
    double a[N][N] = {0}, res = 1;
     
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= n; ++j)
        {
            scanf("%lf", &a[i][j]);
            if (i == j) continue;
            if (i < j && fabs(a[i][j] - 1) > eps) res *= 1 - a[i][j]; 
            if (fabs(a[i][j] - 1) > eps) a[i][j] = -a[i][j] / (1 - a[i][j]); 
            else a[i][j] = -a[i][j];
        }
    }
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            if (i != j) a[i][i] -= a[i][j];
    printf("%.8lf
", fabs(res * Solve(a, n - 1)));
    return 0;
}