题面被改成了个猪。。。
T1猪猪划船(boat)
【题目描述】
6只可爱的猪猪们一起旅游,其中有3只大猪A,B,C,他们的孩子为3只小猪a,b,c。由于猪猪们十分凶残,如果小猪在没有父母监护的情况下,和其他的大猪待在一起,就会被吃掉。
拦在他们面前的是一条大河,河上有一只只有1个船桨且限载2只猪的小船,只有A,B,C,a会划船。他们独自划船单程需要的时间为tA,tB,tC,ta,如果搭载另一只猪时间翻倍。你需要求出所有猪猪过河的最短时间。
【输入数据】
一行,4个整数,tA,tB,tC,ta。
【输出数据】
一行,一个整数,表示最短时间。
【样例输入】
10 10 10 10
【样例输出】
220
【数据范围】
对于20%的数据:tA=tB=tC=ta
对于60%的数据:ta<=tA<=tB<=tC
对于100%的数据:tA,tB,tC,ta<=100
【题解大意】
写的时候没推懂样例。然后因为样例给的是tA=tB=tC=ta,所以交了一个无脑的20分,直接输出22*t。
一直到讲之前也还是没弄懂样例。。。
【code】

//boat.20 #include<bits/stdc++.h> using namespace std; #define ll long long #define ull unsigned long long #define rep(k,i,j) for(int k = i;k <= j; ++k) #define FOR(k,i,j) for(int k = i;k >= j; --k) inline void file(){ freopen("boat.in","r",stdin); freopen("boat.out","w",stdout); } inline int read(){ int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0'; ch=getchar();} return x*f; } const int mxn = 200; int val[5]; inline int A(int x){return x&(1<<1)>0;} inline int B(int x){return x&(1<<2)>0;} inline int C(int x){return x&(1<<3)>0;} inline int a(int x){return x&(1<<4)>0;} inline int b(int x){return x&(1<<5)>0;} inline int c(int x){return x&(1<<6)>0;} inline bool check(int x){ if(A(x)!=a(x)) if(a(x)==B(x)||a(x)==C(x)) return 0; if(B(x)!=b(x)) if(b(x)==A(x)||a(x)==C(x)) return 0; if(C(x)!=c(x)) if(c(x)==A(x)||c(x)==B(x)) return 0; return 1; } bool v[mxn]; int d[mxn]; queue<int>q; inline void wor(int x,int y,int z){ if(!check(y)) return; if(d[y] > d[x]+z){ d[y] = d[x]+z; if(!v[y]) q.push(y),v[y] = 1; } } inline void spfa(){ memset(d,0x3f,sizeof(d)); memset(v,0,sizeof(v)); v[0] = 1,d[0] = 0; q.push(0); while(q.size()){ int x = q.front(); q.pop(); if(x&1){ rep(i,1,4) if(x&(1<<i)) rep(j,1,6) if(x&(1<<j)) if(i==j) wor(x,x^(1<<i)^1,val[i]<<1); else wor(x,x^(1<<i)^(1<<j)^1,val[i]<<1); }else{ rep(i,1,4) if(!(x&(1<<i))) rep(j,1,6) if(!(x&(1<<j))) if(i==j) wor(x,x^(1<<i)^1,val[i]<<1); else wor(x,x^(1<<i)^(1<<j)^1,val[i]<<1); } } } int main(){ // file(); rep(i,1,4) val[i] = read(); spfa(); printf("%d ",d[(1<<7)-1]); return 0; }
T2小猪星球(planet)
【题目描述】
小猪所在的星系有n个星球,用1~n标号,其中有一些星球之间有单向的隧道相连。由于超时空隧道的存在,通过一个隧道的时间可能为0或负数。现在小猪们决定从1号星球出发,沿着最短路径到达n号星球。
科学家猪小聪发明了一种神奇的装置,使得飞船在每个隧道中运行的时间都增加一个相同的常数(可以为0或负数),你需要确定这个常数使得旅途的总时间非负且最小。
【输入数据】
输入文件包含多组数据,第一行为数据组数T。
对于每一组数据,第一行两个整数V,E,表示星球的个数和隧道的个数。接下来E行,每行3个整数i,j,t,表示从i号星球到j号星球有一条耗时为t的单向隧道。
【输出数据】
共T行,每行一个整数,表示从1号星球到n号星球最短的时间。如果不能从1号星球到达n号星球,输出-1。
【样例输入】
1
4 5
1 2 1
1 3 1
2 3 -3
3 1 1
3 4 1
【样例输出】
2
【样例解释】
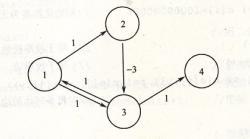
如果不使用科技(也可以理解成是使用科技,但确定常数为0,所有的隧道时间不变),则1->2->3->1->2->3……->4的时间为负无穷,不符合要求。若使用科技,确定常数为1,则1->2->3->4的最短时间为2。
【数据范围】
对于100%的数据,N<=100,E<=N(N+1)/2,|t|<=10^5,i,j<=N
友情提示:可能有重边和自环
【题解大意】
写了两个小时还是爆零的题,真是令人开心。
【code】

//planet #include<bits/stdc++.h> using namespace std; #define inf 1<<30 #define ll long long #define ull unsigned long long #define rep(k,i,j) for(int k = i;k <= j; ++k) #define FOR(k,i,j) for(int k = i;k >= j; --k) inline void file(){ freopen("planet.in","r",stdin); freopen("planet.out","w",stdout); } inline int read(){ int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0'; ch=getchar();} return x*f; } const int mxn = 105; const int lim = 1e5; int T,V,E; bool v[mxn],vis[mxn]; struct edge{int nxt,y,v;}e[lim]; struct eg{int nxt,y;}e1[lim]; int to[mxn],len; inline void add(int xx,int yy,int zz){ e[++len].nxt = to[xx]; to[xx] = len; e[len].y = yy; e[len].v = zz; } int to1[mxn],len1; inline void add1(int x,int y){ e1[++len1].nxt = to1[x]; to1[x] = len1; e1[len1].y = y; } int d[mxn]; queue<int> q; int cnt[mxn]; bool a[mxn][mxn]; inline void dfs(int x){ vis[x] = 1; for(int i = to1[x]; i;i = e1[i].nxt){ int y = e1[i].y; if(!vis[y]) dfs(y); } } inline void Floyd(){ memset(vis,0,sizeof(vis)); rep(k,1,V)rep(i,1,V)rep(j,1,V) a[i][j] |= a[i][k]&a[k][j]; //连通为 1,不连通为 0 rep(i,1,V-1) if(!a[i][V]) vis[i] = 1; } inline bool spfa(int dt){ memset(cnt,0,sizeof(cnt)); memset(d,0x3f,sizeof(d)); memset(v,0,sizeof(v)); v[1] = 1,d[1] = 0,cnt[1] = 1; q.push(1); while(q.size()){ int x = q.front(); q.pop(); v[x] = 0; for(int i = to[x]; i;i = e[i].nxt){ int y = e[i].y,z = e[i].v+dt; if(vis[y]) continue; if(d[y] > d[x]+z){ d[y] = d[x]+z; cnt[y] = cnt[x]+1; if(cnt[y] > V) return 0; if(!v[y]) q.push(y),v[y] = 1; } } } return d[V]>=0; } int l,r,m; inline int wor(){ if(vis[1]) return -1; l = -lim,r = lim; while(l+1<r){ m = l+r >>1; spfa(m)?r = m:l = m+1; } if(spfa(l)) return d[V]; spfa(r); return d[V]; } inline void clear(){ len = 0,len1 = 0; memset(to,0,sizeof to); memset(to1,0,sizeof to1); memset(vis,0,sizeof vis); } int main(){ // file(); T = read(); while(T--){ V = read(),E = read(); memset(a,0,sizeof(a)); clear(); while(E--) { int i = read(),j = read(),t = read(); a[i][j] = 1; add(i,j,t); // add1(j,i); } // dfs(V); Floyd(); printf("%d ",wor()); } return 0; }
T3小猪送货(deliver)
【题目描述】
小猪所在的星系有n个星球从左到右排成一排,用1~n标号。每个星球有建设有一个工厂,住着若干居民。猪粮是猪猪星系的重要的物资,第i个城市的工厂能够生产pi个单位的猪粮,第i个城市最多可以卖出si个单位猪粮。对于任意1<=i<j<=n,存在着一条从i到j的单向道路,最多可以通过这条道路运输c个单位的猪粮,你需要计算最多能够卖出多少猪粮。
【输入数据】
第一行两个整数n,c
第二行n个整数,第i个整数表示pi
第三行n个整数,第i个整数表示si
【输出数据】
一行,一个整数,表示最多可以卖出的猪粮的单位数
【样例输入1】
5 1
7 4 2 1 0
1 2 3 4 5
【样例输出1】
12
【样例输入2】
4 3
13 10 7 4
4 7 10 13
【样例输出2】
34
【数据范围】
对于20%的数据:c=0
对于60%的数据:n<=100
对于100%的数据:n<=10000,0<=c,pi,si<=10^9
【题解大意】
拿了c=0的部分分,每次加上min(p[i],s[i])就行,正确性显然。
本题来源:codeforces 724E
【code】

#include<bits/stdc++.h> using namespace std; #define inf 1<<30 #define ll long long #define ull unsigned long long #define rep(k,i,j) for(int k = i;k <= j; ++k) #define FOR(k,i,j) for(int k = i;k >= j; --k) inline void file(){ freopen("deliver.in","r",stdin); freopen("deliver.out","w",stdout); } inline int read(){ int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0'; ch=getchar();} return x*f; } const int mxn = 1e4+5; int p[mxn],s[mxn]; int n,c; int f[mxn][mxn]; int main(){ file(); n = read(),c = read(); rep(i,1,n) p[i] = read(); rep(i,1,n) s[i] = read(); rep(i,1,n) f[0][i] = f[1][i] = inf; f[1][0]=p[1],f[1][1]=s[1]; rep(i,2,n){ f[i&1][0] = f[i&1^1][0]+p[i]; rep(j,1,n){ f[i&1][j] = min(f[i&1^1][j]+j*c+p[i],f[i&1^1][j-1]+s[i]); } } int minx = inf; rep(i,0,n) minx = min(minx,f[n&1][i]); printf("%d ",minx); return 0; }
T4小猪数数(math)
【题目描述】
猪小聪和猪小明在一个小时的时间里,A完了前三题,他们无聊地说:“咱们来玩个游戏消磨时间吧……”
在这个游戏中,猪小聪和猪小明每个人手上有一台电脑,一开始双方的电脑上的数字都是1。现在猪小聪和猪小明按照任意的顺序执行操作a=a+b(其中a为自己电脑上的数字,b为对方电脑上的数字),例如按照小聪-小明-小明执行后双方的数字为2 5。
现在在他们玩了若干轮之后,双方电脑上的数字为N M,可惜的是他们忘记了他们到底玩了多少轮,你需要求出他们至少玩了多少轮。
【输入数据】
2个整数,表示N,M。
【输出数据】
1个整数,表示最少玩过的轮数。如果根本不可能出现符合要求的结果,输出-1。
【样例输入1】
2 5
【样例输出1】
3
【样例输入2】
2 2
【样例输出2】
-1
【数据范围】
对于30%的数据,1<=N,M<=10
对于60%的数据,1<=N,M<=1000
对于100%的数据:N,M和ans均不会爆long long (ans表示输出的答案)
【题解大意】
考虑怎么把给定的两个数给弄回去,辗转相减之类的就好了,然后看最后能不能减到n=1,m=1
最后一题这么来好假。。。
【code】

#include<bits/stdc++.h> using namespace std; #define ll long long #define ull unsigned long long #define rep(k,i,j) for(int k = i;k <= j; ++k) #define FOR(k,i,j) for(int k = i;k >= j; --k) inline void file(){ freopen("math.in","r",stdin); freopen("math.out","w",stdout); } inline int read(){ int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0'; ch=getchar();} return x*f; } ll n,m,tot = 0; inline void work(){ bool f = 1; while(m>0&&n>0){ if(m==1&&n==1) break; m -= n; if(m==0||n==0) { f = 0; break; } ++tot; if(m<n) swap(m,n); } if(f) printf("%lld ",tot); else puts("-1"); } int main(){ // file(); scanf("%lld %lld",&n,&m); if(n>m) swap(n,m); if(n==m&&n!=1) { puts("-1"); return 0; } if(n==m&&n==1){ puts("0"); return 0; } work(); return 0; }
