题目:
The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.
输入:
The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.
输出:
For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.
样例:
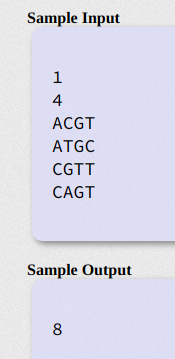
分析:公共序列只要满足子序列的排列顺序就行;
IDA*算法,逐渐放大搜索的宽度,并用估价函数(估计仍需匹配的深度)进行剪枝
1 #include<iostream> 2 #include<sstream> 3 #include<cstdio> 4 #include<cstdlib> 5 #include<string> 6 #include<cstring> 7 #include<algorithm> 8 #include<functional> 9 #include<iomanip> 10 #include<numeric> 11 #include<cmath> 12 #include<queue> 13 #include<vector> 14 #include<set> 15 #include<cctype> 16 #define PI acos(-1.0) 17 const int INF = 0x3f3f3f3f; 18 const int NINF = -INF - 1; 19 typedef long long ll; 20 using namespace std; 21 int n, deep, ans;//deep记录深度, ans记录答案 22 string seq[10];//n个子序列 23 int siz[10];//n个子序列对应的长度 24 char DNA[5] = {'A', 'C', 'G', 'T'}; 25 void dfs(int rec, int *pos)//当前匹配到的公共序列的个数, 个子序列匹配到的位置 26 { 27 if (rec > deep) return;//如果大于搜索深度即加深深度结束 28 int hx = 0;//估计剩余需匹配的深度 29 for (int i = 0; i < n; ++i) 30 { 31 int temp = siz[i] - pos[i]; 32 hx = max(temp, hx);//剩余需匹配深度为子序列未匹配部分最大长度 33 } 34 if (!hx)//如果剩余需匹配为0即完成 35 { 36 ans = rec; 37 return; 38 } 39 if (hx + rec > deep) return;//如果已匹配深度加估计剩余需匹配深度大于限制深度即加深深度结束 40 for (int i = 0; i < 4; ++i)//公共序列下一个值可能的四个 41 { 42 int tmp[10];//类似BFS的操作 43 int flag = 0;//flag进行了一次剪枝,如果DNA[i]不能匹配当前任何子序列的下一个值则不再进行DFS直接舍弃(从3500ms优化到1200ms) 44 for (int j = 0; j < n; ++j) 45 { 46 if (seq[j][pos[j]] == DNA[i])//子序列j的第pos[j](匹配到位置)若等于 47 { 48 flag = 1; 49 tmp[j] = pos[j] + 1;//匹配成功下次考虑该子序列的下一个位置 50 } 51 else tmp[j] = pos[j]; 52 } 53 if (flag) 54 dfs(rec + 1, tmp); 55 if (ans != -1) return; 56 } 57 } 58 int main() 59 { 60 int T; 61 cin >> T; 62 while (T--) 63 { 64 cin >> n; 65 int maxn = 0;//n个子序列的最大长度 66 for (int i = 0; i < n; ++i) 67 { 68 cin >> seq[i]; 69 siz[i] = seq[i].length();//估价函数需要,记录n个子序列对应长度 70 maxn = max(maxn, siz[i]); 71 } 72 deep = maxn; 73 int pos[10];//子序列匹配到的位置 74 memset(pos, 0, sizeof(pos)); 75 ans = -1; 76 while (1) 77 { 78 dfs(0, pos); 79 if (ans != -1) break; 80 deep++;//每进行一次DFS,若未匹配完成则加深搜索深度继续进行 81 } 82 cout << ans << endl; 83 } 84 return 0; 85 }