【HDU-2049】不容易系列之(4)——考新郎

原题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2049
标签：组合数学/错排
难度：中

解题记录

N对新人，M对选错，问一共有多少种可能，

先用排列组合公式计算C(M，N)，即从N对中挑选M对有多少种不同的挑选方法

然后计算这M对一共有多少种错排方法es(M)

阶乘公式

我一开始写用了很土的循环，封装了一个函数

long long fac(int n) {
    long long res = 1;
    while (n) {
        res *= n;
        n--;
    }
    return res;
}

网上发现大佬是直接维护一个数组a[N]，然后一边循环计算出来后，直接使用

排列组合公式

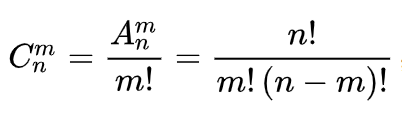
long int C(int m, int n) {
    return fac(n)/fac(m)/fac(n-m);
}

错排公式

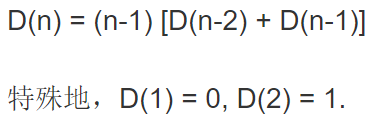
这里使用类似动态规划的方法理解，D[N]代表N个错排的可能数量

转化为考虑，向已经错排的D[N-1]中再加入一对元素的场景

假如已经有错排 D[N-1]，则第N个元素可以与N-1个中任意一对元素交换，结果仍然是错排

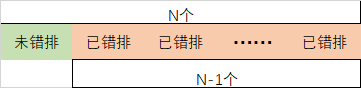
假如已有错排D[N-2]

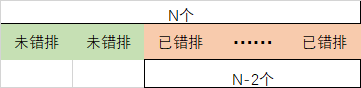
此时只要把两个没有错排的元素交叉错排即可，这种情况有N-1种（从N-1个中挑出1个没有错排的元素）

对于D[N-3]的情况，已经包含在上面两种情况中

最终AC代码

#include <stdio.h>

// 阶乘公式 
long long fac(int n) {
    long long res = 1;
    while (n) {
        res *= n;
        n--;
    }
    return res;
}

// 排列组合公式 
long int C(int m, int n) {
    return fac(n)/fac(m)/fac(n-m);
}

// 错排公式 
long long es[21];
long long es_init(void) {
    int i;
    es[1] = 1;
    es[2] = 1;
    es[3] = 2;
    for (i = 4; i <= 20; i++) {
        es[i] = (i - 1)*(es[i-1] + es[i-2]);
    }
}

int main(void)
{
    int i, j;
    int T;
    es_init();
    
    scanf("%d", &T);
    
    while(T--) {
        int N, M;
        scanf("%d%d",&N, &M);
        printf("%lld
", C(M,N)*es[M]);
    }
    
    return 0;
}