【算法】动态规划

理解

---

动态规划是将原始问题分解为若干个子问题，对子问题进行求解，并记录下子问题的结果，当求解包含已经解决的子问题的原问题时，返回子问题的结果即可

基本概念

---

转移方程、边界

最优子结构

引例

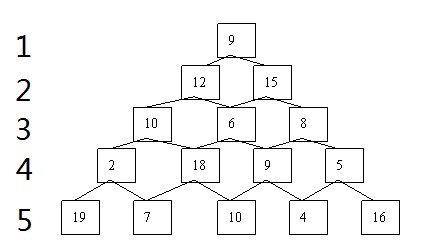
数塔问题

在如上数塔中，选取一条路径使得路径上的数字和最大

解：

设数塔表示为$f[i][j]$，$dp[i][j]$表示选择了$f[i][j]$能得到的最大的和，得到转移方程为：

(dp[i][j] = max{(dp[i+1][j], dp[i+1][j+1])}+f[i][j])

边界为:

(dp[n][j] = f[n][j])

递归求解即可

斐波那契数列求解

走楼梯

典型问题

---

最大连续子列和

• 在数列$n_1, n_2, ... , n_K$中，求出$n_i + n_{i+1} + ... + n_j$ 的最大值

• dp数组：$dp[i]$表示以$n_i$结尾的子列中子列和的值

• 转移方程和边界

  (dp[i] = max(dp[i - 1] + a[i], dp[i]))

  (dp[i] = a[i])

最长不降子序列（LIS）

• 序列可以不连续

• dp数组：$dp[i]$表示以$A[i]$结尾的LIS长度

• 状态转移方程：

  当$A[i]$前的元素$A[j]$都比$A[i]$大，(dp[i] = 1)

  否则：(dp[i] = max(dp[j] + 1))

  综上：(dp[i] = max(1, dp[j] + 1), 0 leq j< i,A[j] leq A[i])

  边界：(dp[i] = 1)

最长公共子序列（LCS）

• 子序列可以不连续

• dp数组：$dp[i][j]$表示$A[i], B[j]$前LCS的长度

• 状态转移方程和边界

  当$A[i] == B[j]$：(dp[i][j] = dp[i - 1][j - 1] + 1)

  当$A[i] ！= B[j]$：(dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]))

  边界：(d[i][0] = d[0][j] = 0)

• 注意字符串下标从1开始

最长回文串

• 求解长度最长的回文串

• dp数组：$dp[i][j] = 1$表示$A[i], ..., A[j]$是回文串，$dp[i][j] = 0$表示$A[i], ..., A[j]$是不是回文串

• 状态转移方程：

  当$A[i] == A[j]$：(dp[i][j] = dp[i + 1][j-1])

  当$A[i] != A[j]$：(dp[i][j] = 0)

  边界：(d[i][i] = 1, d[i][i+1] = (s[i] == s[i+1]) ? 1 : 0)

• 求解方法：按照子串长度从1到$strlen(s)$递推

DAG最长路

不定终点

• dp数组：$dp[i]$表示以$i$为起点的最长长度

• 状态转移方程：

  

  (dp[i] = max(dp[j] + len_{i ightarrow j})

  边界：(dp[i] = 0)

• 实现

  计算路径长度

  int DP(int v){
      if(dp[v] > 0)return dp[v];
      for(int i = 0; i < G[v].size(); ++i){
          int u = G[v][i], temp = DP[u] + G[v][i].w;
          if(temp > dp[v])dp[v] = temp;
      }
      return dp[v];
  }
  

  计算关键路径

  增加一个choice数组，记录节点 i 的后继节点

  int DP(int v){
      if(dp[v] > 0)return dp[v];
      for(int i = 0; i < G[v].size(); ++i){
          int u = G[v][i], temp = DP[u] + G[v][i].w;
          if(temp > dp[v]){
             dp[v] = temp;
              choice[v] = u;
          }
      }
      return dp[v];
  }
  

定终点

终点固定为T，总体和不定终点一样，不同在边界条件：

(dp[T] = 0, dp[i] = -inf (i eq T))

实例

在给定的DAG中寻找关键路径

//http://codeup.cn/problem.php?cid=100000624&pid=0
#include<iostream>
#include<cstdio>
#include<vector>
#include<unordered_map>
#include<string>
#include<stack>
#include<queue>
#include<set>
#include<algorithm>
using namespace std;
struct node{
    int v, w;
};
const int nmax = 20;
vector<node>G[nmax];
unordered_map<char, int>mp;
char rmp[nmax];
int cnt = 0;
void getIndex(char ch){
    auto it = mp.find(ch);
    if(it == mp.end()){
        mp[ch] = cnt;
        rmp[cnt] = ch;
        cnt++;
    }
}
int dp[nmax], choice[nmax];
int DP(int i){
    if(dp[i] > 0)return dp[i];
    for(int j = 0; j < G[i].size(); ++j){
        int v = G[i][j].v, temp = DP(v) + G[i][j].w;
        if(temp > dp[i]){
            dp[i] = temp;
            choice[i] = v;
        }
    }
    return dp[i];
}
void printPath(int s){
    while(choice[s] != -1){
        printf("(%c,%c) ", rmp[s], rmp[choice[s]]);
        s = choice[s];
    }
}
void init(){
    for(int i = 0; i < nmax; ++i){
        G[i].clear();
        dp[i] = 0;
        choice[i] = -1;
    }
    mp.clear();
    cnt = 0;
}
int main()
{
    int cnt = 0;
    cin>>cnt;
    for(int i = 0; i < cnt; ++i){
        init();
        int n, m;
        cin>>n>>m;
        char ch;
        for(int j = 0; j < n; ++j){
            cin>>ch;
            getIndex(ch);
        }
        for(int j = 0; j < m; ++j){
            char ch1, ch2;
            int w;
            cin>>ch1>>ch2>>w;
            G[mp[ch1]].push_back({mp[ch2], w});
        }
        int ans = 0, s;
        for(int j = 0; j < n; ++j){
            int temp = DP(j);
            if(temp > ans){
                ans = temp;
                s = j;
            }
        }
        printPath(s);
        printf("%d
", ans);
    }
    return 0;
}

动态规划

01背包

• 问题描述：

  有n件物品，每件物品重量为$w[i]$，价值为$c[i]$，$1leq ileq n$，给定容量为$V$的背包，求解使背包内物品总价值最大的方案

• 解决方案：

  • 递归搜索

    //未计算价值
    const int nmax = 10010;
    int num[nmax] = {0};
    vector<int>ans, temp;
    bool flag = false;
    void dfs(int index, int sum, int M, int n){
        if(sum > M || index > n)return;
        if(sum == M){
            ans = temp;
            flag = true;
            return;
        }
        if(flag)return;
        temp.push_back(index);
        dfs(index + 1, sum + num[index], M, n);
        temp.pop_back();
        if(flag)return;
        dfs(index + 1, sum, M, n);
    }
    

  • 动态规划

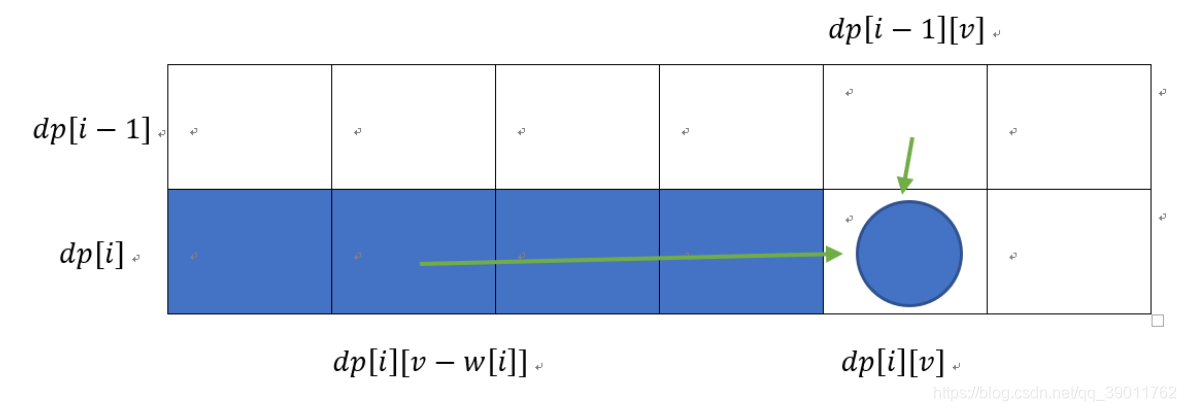
  设数组$dp[i][v]，0 leq ileq n, w[i] leq v leq V$表示前$i$件物品放入容量为$v$的背包中获得的最大价值，状态转移方程为：(dp[i][v] = max(dp[i-1][v], dp[i - 1][v-w[i]] + c[i]))，边界条件为：(dp[0][v] = 0)

  for(int i = 1; i <= n; ++i){
      for(int v = w[i]; v <= V; ++v){
          dp[i][v] = max(dp[i - 1][v], dp[i - 1][v - w[i]] + c[i]);
      }
  }
  

  求解出dp数组后，遍历$dp[n][v]$，取最大值即为能得到的最大价值

  注：

  1. dp数组的求解

  在求解$dp[i][v]$时，只与$dp[i-1][v]$和$dp[i][v - w[i]]$的状态有关，省去$i$的维度，转移方程写作：(dp[v] = max(dp[v], dp[v - w[i]] + c[i]), w[i]leq v leq V)

  求解时倒着枚举v 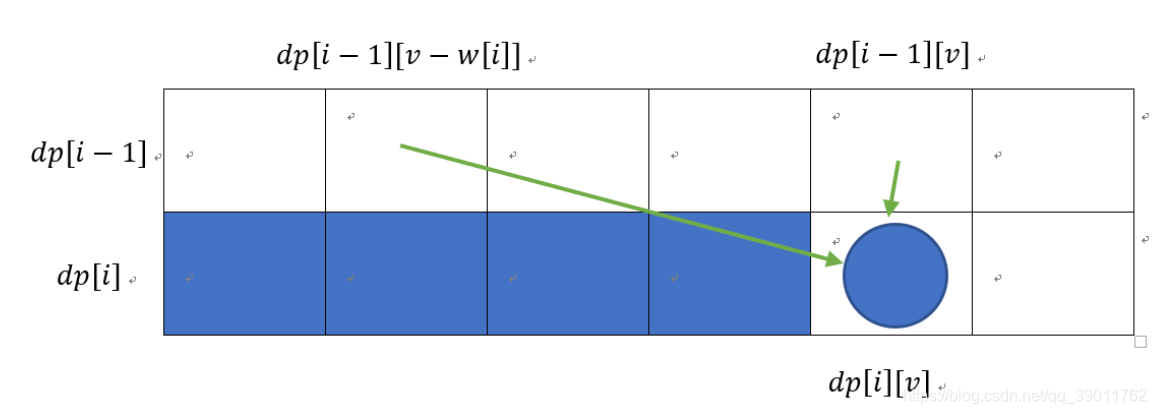如果正向枚举，则前一个状态的$dp[v-w[i]]$会被覆盖

2. 记录选择方式

开一个数组$choice[i][v]$，当$choice[i][v] == 1$时表示前$i$件物品取得最大值时选择了第$i$件，否则就没选，最终倒着枚举$choice[i][v], v = argmax_{vleq V}(dp[v]) $就能获得选择的方案

例子：

（PAT1068）第一行给出货币个数n和应付金额m，第二行给出n个货币的面额，求出付钱的方式，如果方式不唯一，给出字典序最小的方案，如果没有答案，输出"No Solution"

分析：

（1）要求的答案是$V_1 + V_2 +...+V_k == m $，因此应付金额m对应背包容量V，面额对应物品的质量，同时面额也对应物品的价值，因此无解的判定条件时$dp[m] != m$

（2）要输出字典序最小的答案，先将数组逆序（因为滚动数组中v是逆序枚举），当$dp[v - w[i]] + c[i] == dp[v]$时，选择放第 i 件物品（不放得到的会是字典序最大的）

//求dp数组
for(int i = 1; i <= n; ++i){
    for(int v = m; v >= num[i]; --v){
        if(dp[v - num[i]] + num[i] >= dp[v]){
            dp[v] = dp[v - num[i]] + num[i];
            choice[i][v] = true;
        }
    }
}
//输出路径
bool flag = false;
for(int i = n; i >= 1; --i){
    if(choice[i][m] == true){
        if(flag)printf(" ");
        printf("%d", num[i]);
        flag = true;
        m -= num[i];//注意更新v
    }
}

完全背包

• 问题描述：

  有n种物品，每件物品重量为$w[i]$，价值为$c[i]$，$1leq ileq n$，给定容量为$V$的背包，求解使背包内物品总价值最大的方案

• 解决方案

  分析方法同0-1背包，转移方程为：(dp[i][v] = max(dp[i-1][v], dp[i][v-w[i]] + c[i]))

• 滚动数组可以正向或者逆向枚举

  (max(dp[v], dp[v - w[i]] + c[i]), w[i]leq v leq V)