- Count Complete Tree Nodes
Given a complete binary tree, count the number of nodes.
Note:
Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Example:
Input:
1
/
2 3
/ /
4 5 6
Output: 6
解法1 一般的计算节点数目方法,count(root) = 1 + count(root->left) + count(root->left)
class Solution {
public:
int countNodes(TreeNode* root) {
if(root == NULL)return 0;
return 1 + countNodes(root->left) + countNodes(root->right);
}
}
解法2 先序/中序/后序遍历一次
class Solution {
public:
int countNodes(TreeNode* root) {
int ans = 0;
pre(root, ans);
return ans;
}
void pre(TreeNode *root, int &ans){
if(root == NULL)return;
ans++;
pre(root->left, ans);
pre(root->right, ans);
}
};
解法3 考虑到完全二叉树的特点:对于每一个节点来说,总有一边是满二叉树,高度为(d)满二叉树共有(2^d-1)个节点
class Solution {
public:
int countNodes(TreeNode* root) {
int l_h = get_left_h(root);
int r_h = get_right_h(root);
if(l_h == r_h)return pow(2, l_h) - 1;
return 1 + countNodes(root->left) + countNodes(root->right);
}
int get_left_h(TreeNode *root){
int d = 0;
while(root){
d++;
root = root->left;
}
return d;
}
int get_right_h(TreeNode *root){
int d = 0;
while(root){
d++;
root = root->right;
}
return d;
}
};
解法4 考虑完全二叉树的特点:只有最后一层是不满的,采用二分查找确定是从哪里分割的,即寻找第一个没有出现在叶子节点中的节点编号
-
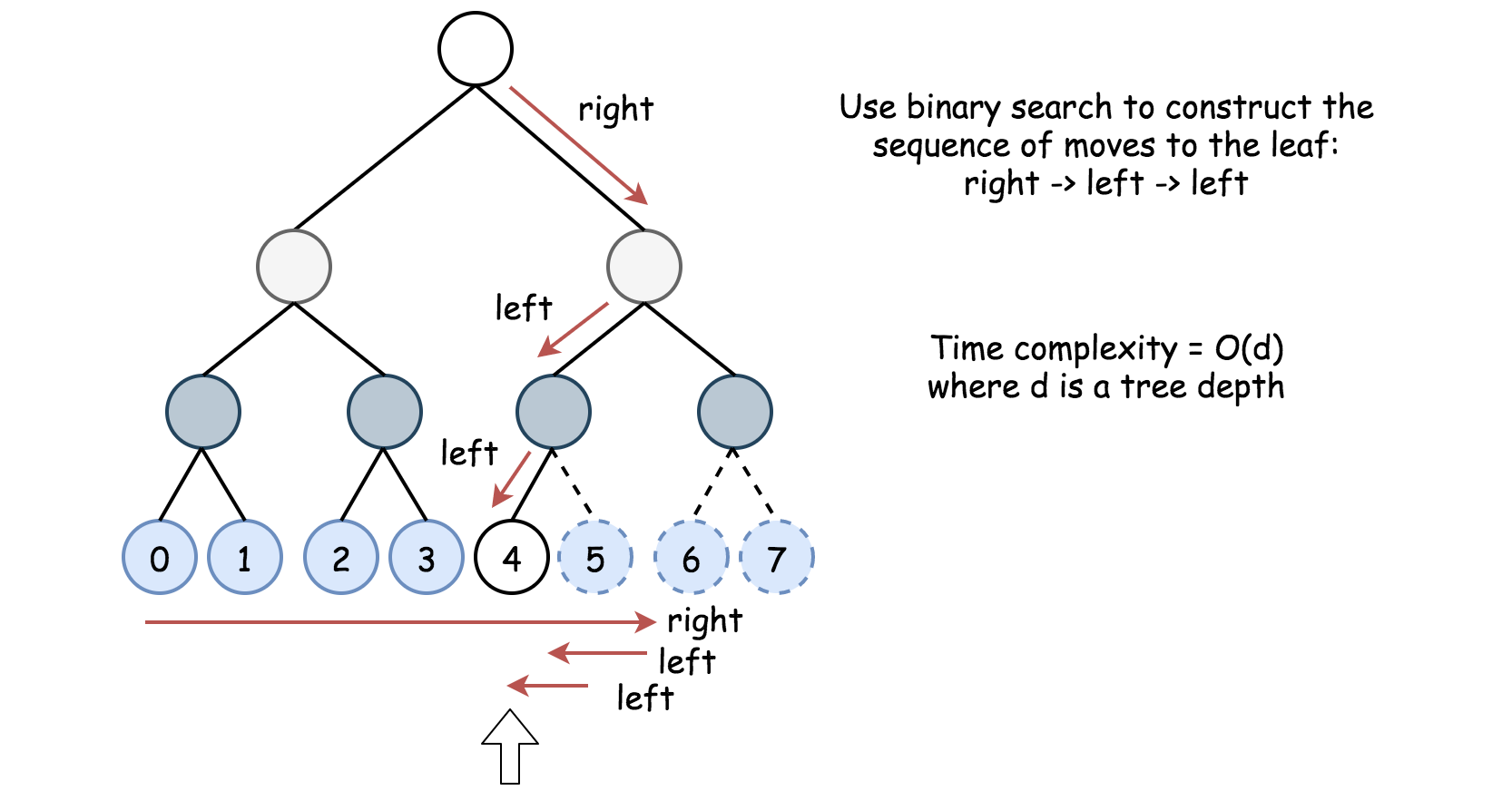
如何判断一个叶子节点是否存在
将叶子节点编号为([0, 1, ..., 2^d -1]),根节点将叶子节点分成了([0, frac{2^d-1}{2}-1])和([frac{2^d-1}{2}, 2^d-1])两部分,查找编号为idx的叶子时:
- idx <= mid, root = root->left
- idx > mid, root = root->right
-
如何查找第一个不存在的叶子结点的编号
假设第一个不存在的叶子结点在区间([l, r])中,判断中点(mid = (l + r) / 2)
- exist(mid) == true :中点及左侧区间被排除
- exist(mid) == false : 右侧区间被排除
class Solution {
public:
int countNodes(TreeNode* root) {
int l_h = get_left_h(root);
int r_h = get_right_h(root);
if(l_h == r_h)return pow(2, r_h) - 1;
int l = 0, r = pow(2, r_h) - 1;
while(l < r){
int mid = (l + r) / 2;
if(exist(mid, r_h, root)){
l = mid + 1;
}else{
r = mid;
}
}
return pow(2, r_h) + l-1;
}
bool exist(int val, int d, TreeNode *root){
int l = 0, r = pow(2, d)-1;
TreeNode *cur = root;
for(int i = 0; i < d; ++i){
int mid = (l + r) / 2;
if(val <= mid){
r = mid;
cur = cur->left;
}else{
l = mid + 1;
cur = cur->right;
}
}
return cur != NULL;
}
int get_left_h(TreeNode *root){
int d = 0;
while(root){
d++;
root = root->left;
}
return d;
}
int get_right_h(TreeNode *root){
int d = 0;
while(root){
d++;
root = root->right;
}
return d;
}
};