https://www.cnblogs.com/violet-acmer/p/10146350.html
题意:
有一块 n*m 的棋盘,初始,黑白块相间排列,且左下角为白块。
给出两个区间[ (x1,y1) , (x2,y2) ] 和 [ (x3,y3) , (x4,y4) ],第一个区间全部涂成白色,第二个区间全部涂成黑色,且颜色会覆盖。
求两块区间按照要求涂完后白块和黑快的个数?
题解:
我的想法如下:
先求出初始的黑块个数,然后,求出第一个区间减少的黑块个数,再求出第二个区间增加的黑块个数,求出黑块个数后,白块个数也就出来了。
具体求法:
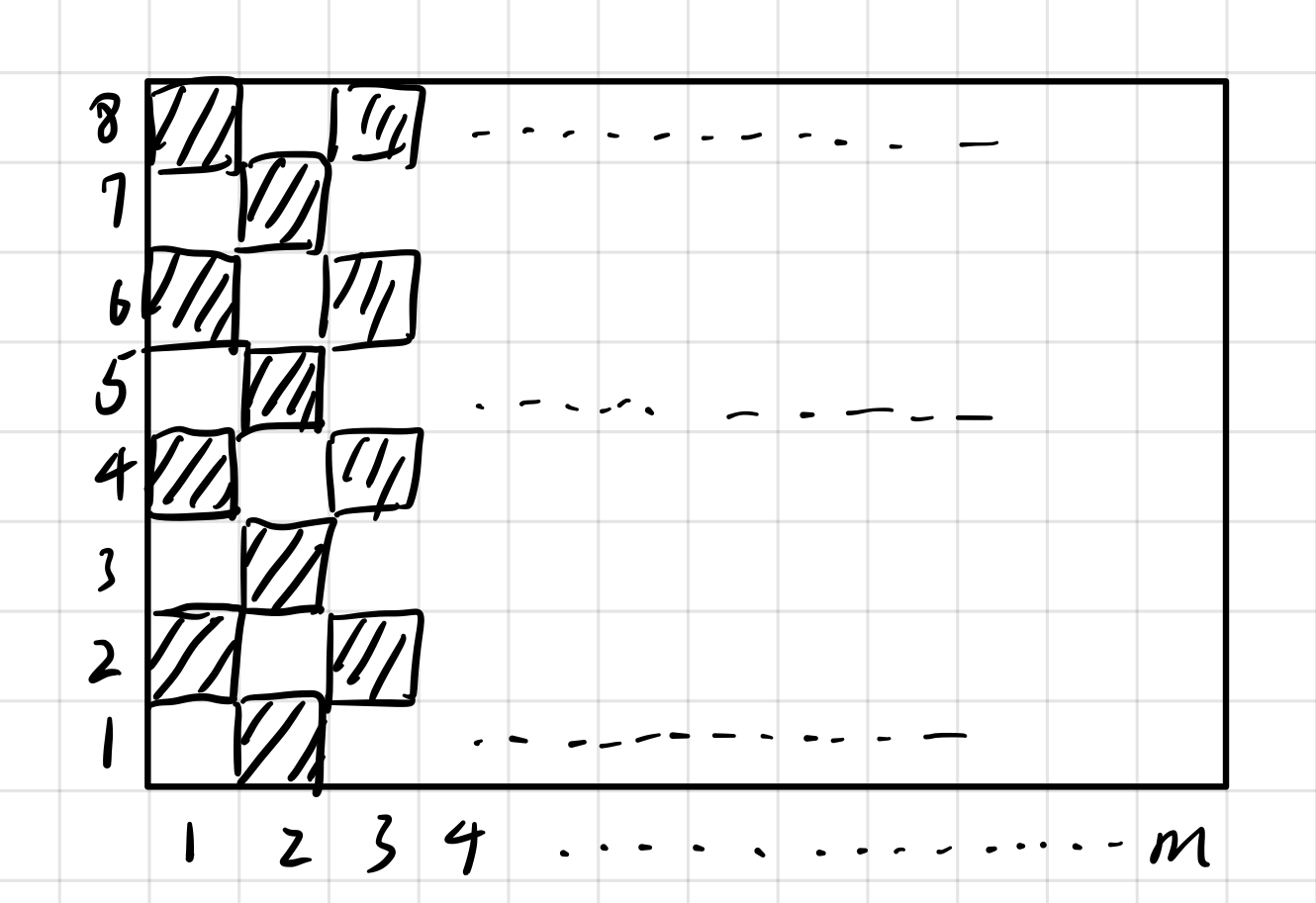
如何求出初始黑块个数呢?
定义变量 totBlack 为黑块个数。
看图,你会发现第一列与第二列黑块的总和 ==8(n)
也就是说,前m列会有(m/2)*8个黑块,如果m为奇数,那么就会剩下最后一列不能配对,而最后一列的黑块的个数就是 n/2;
在经过观察,你会发现,黑块的坐标加和 x+y 为奇数,知道这个后,问题将变得异常简单。
首先[(x1,y1),(x2,y2)]区间1的所有黑块都会被涂成白块,求出此区间的黑块个数 totBlack1,totBlack -= totBlack1;
而[(x3,y3),(x4,y4)]区间2的所有白块会被涂成黑块,如果区间1和区间2不重合,问题会变得很简单,但,如果重合呢?
先不考虑重合的问题,单纯的求出区间2的白块个数 totBlack3,totBlack += totBlack3;
对于重合的部分,求出重合部分的黑块个数 totBlack4,totBlack += totBlack4;
因为,区间1会把重合部分的黑块变为白块,而区间2在查找白块的时候会忽略重合区间的黑块部分,而这部分正好是少加的。
具体细节看代码。
补充一点计算几何的小知识点,如何求出重合矩形?

此题中给的两个坐标正好是左下和右上,很友好,哈哈哈~~~~~~~
AC代码:

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 #define ll __int64 5 6 ll n,m; 7 struct Node 8 { 9 int x1,y1; 10 int x2,y2; 11 Node(int a=0,int b=0,int c=0,int d=0) 12 { 13 x1=a,y1=b; 14 x2=c,y2=d; 15 } 16 }rec[4]; 17 18 //i == 1 : 查找[(x1,y1),(x2,y2)]黑块个数 19 //i == 2 : 查找[(x3,y3),(x4,y4)]白块个数 20 //i == 3 : 查找重合区间的黑块个数 21 ll Find1(int i) 22 { 23 int totX=rec[i].x2-rec[i].x1+1; 24 int totY=rec[i].y2-rec[i].y1+1; 25 26 ll res=0; 27 if(totX >= 2) 28 res=1ll*totY*(totX>>1); 29 if(totX&1)//如果totX为奇数,那么之前两两配对后,会剩下最后一列没被统计 30 { 31 if(i&1)//查找最后一列黑块个数 32 { 33 if(rec[i].x2&1)//x2为奇,找y为偶的个数 34 res += (totY>>1)+((totY&1) && (rec[i].y1%2 == 0) ? 1:0); 35 else//x为偶数,找y为奇的个数 36 res += (totY>>1)+((totY&1) && (rec[i].y1&1) ? 1:0); 37 } 38 else//查找最后一列白块个数 39 { 40 if(rec[i].x2&1)//x2为奇,找y为奇的个数 41 res += (totY>>1)+((totY&1) && (rec[i].y1&1) ? 1:0); 42 else//x为偶数,找y为偶的个数 43 res += (totY>>1)+((totY&1) && (rec[i].y1%2 == 0) ? 1:0); 44 } 45 } 46 return res; 47 } 48 ll Find2() 49 { 50 ll res=Find1(2); 51 int a=max(rec[1].x1,rec[2].x1),b=max(rec[1].y1,rec[2].y1); 52 int c=min(rec[1].x2,rec[2].x2),d=min(rec[1].y2,rec[2].y2); 53 if(a > c || b > d) 54 return res; 55 56 rec[3]=Node(a,b,c,d); 57 res += Find1(3);//查找重合部分黑块的个数 58 return res; 59 } 60 void Solve() 61 { 62 ll totBlack=0; 63 if(m >= 2) 64 totBlack=n*(m>>1); 65 totBlack += ((m&1) ? (n>>1):0); 66 67 totBlack -= Find1(1);//去掉第一个区间减少的黑块个数 68 totBlack += Find2();//加上第二个区间增加的黑块个数 69 70 printf("%I64d %I64d ",n*m-totBlack,totBlack); 71 } 72 int main() 73 { 74 int t; 75 scanf("%d",&t); 76 while(t--) 77 { 78 int a,b,c,d; 79 scanf("%I64d%I64d",&n,&m); 80 81 scanf("%d%d%d%d",&a,&b,&c,&d); 82 rec[1]=Node(a,b,c,d); 83 84 scanf("%d%d%d%d",&a,&b,&c,&d); 85 rec[2]=Node(a,b,c,d); 86 87 Solve(); 88 } 89 return 0; 90 }
这道题,踩了范围的坑!!!!!
中间定义的一些变量是 int ,但是由于含有乘法操作,中间结果会溢出 int 范围,然后,改了好久好久~~~~~~

一直在wa在text2数据,后来发现,越界了,改成 res=1ll*totY*(totX>>1)才过的
顶着明天Linux考试要挂科的风险再次码了好久好久代码。。。。
考前磨磨枪吧,万一过了呢!!!!!!!
代码有毒,上瘾,哈哈哈,可我就是喜欢啊
