题意:
给出一棵树,每条边都有权值;
给出 m 次询问,每次询问有三个参数 u,v,w ,求节点 u 与节点 v 之间权值 ≤ w 的路径个数;
题解:
昨天再打比赛的时候,中途,凯少和我说,这道题,一眼看去,就是树链剖分,然鹅,太久没写树链剖分的我一时也木有思路;
今天上午把树链剖分温习了一遍,做了个模板题;
下午再想了一下这道题,思路喷涌而出............
首先,介绍一下相关变量:
1 int fa[maxn];//fa[u]:u的父节点 2 int son[maxn];//son[u]:u的重儿子 3 int dep[maxn];//dep[u]:u的深度 4 int siz[maxn];//siz[u]:以u为根的子树节点个数 5 int tid[maxn];//tid[u]:u在线段树中的位置 6 int top[maxn];//top[u]:u所在重链的祖先节点 7 int e[maxn][3];//e[i][0]与e[i][1]有条权值为e[i][2]的边 8 vector<int >v[maxn<<2];//v[i]:存储线段树中i号节点的所有边的权值
(树链剖分,默认来看这篇博客的都会辽,逃)
下面重点介绍一下v[]的作用(将样例2中的权值改为了10):
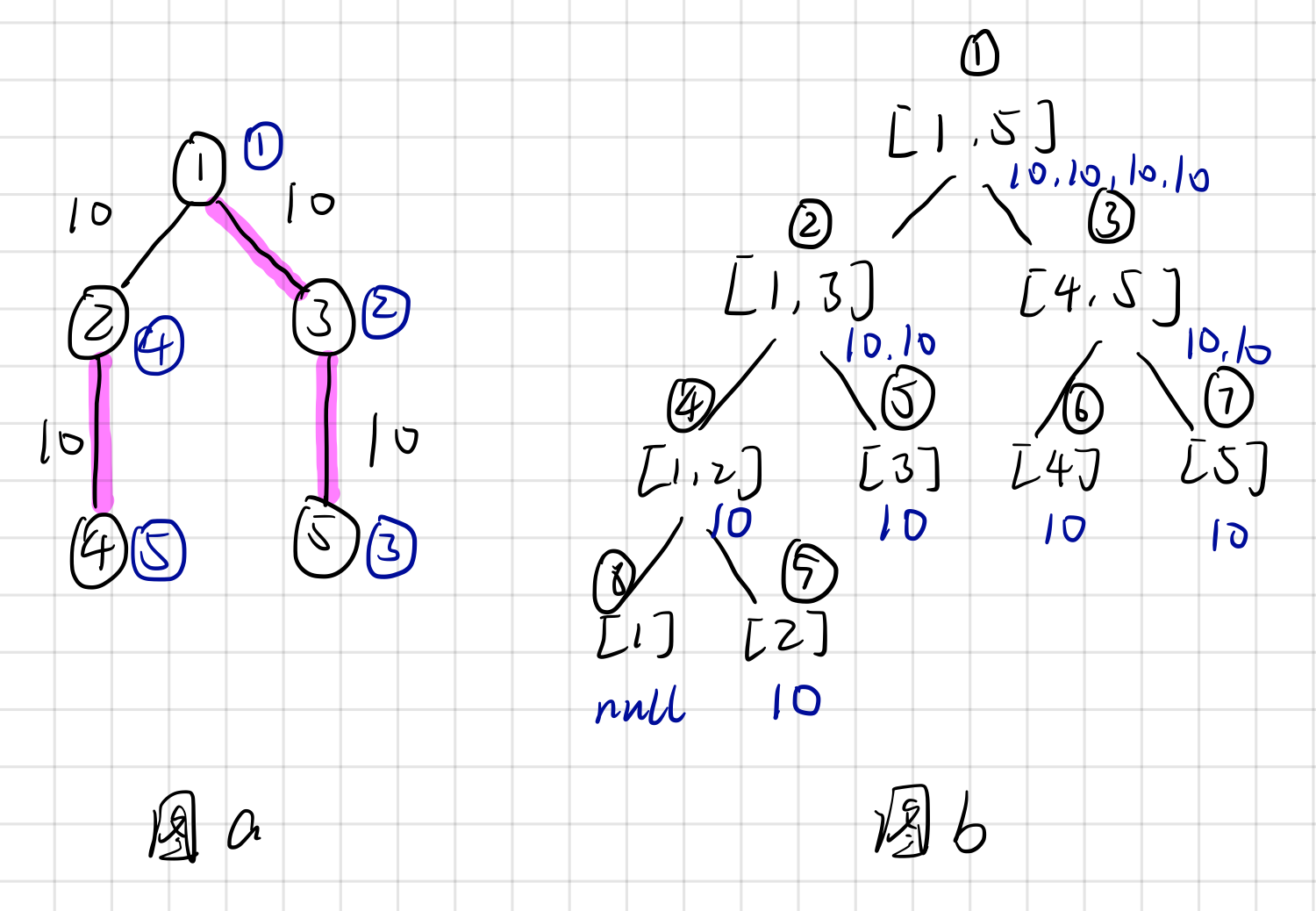
由树链剖分可知(图a,紫色部分代表重链)
tid[1]=1,tid[3]=2,tid[5]=3;
tid[2]=4,tid[4]=5;
那么,线段树维护啥呢?
1 struct SegmentTree 2 { 3 int l,r; 4 int mid() 5 { 6 return l+((r-l)>>1); 7 } 8 }segTree[maxn<<2]; 9 vector<int >v[maxn<<2];//v[i]:存储线段树中i号节点的所有边的权值
对于我而言,此次线段树,主要维护节点 i 的左右区间[l,r],重点是 v[] 中维护的东西;
首先将边权存到线段树中,如何存呢?
对于边 u,v,w ,(假设 fa[v]=u),将 w 存在 v[ tid[ v ] ]中;
看一下Update()函数:
1 //将节点x在线段树中对应的pos位置的v中加入val 2 void Update(int x,int val,int pos) 3 { 4 if(segTree[pos].l == segTree[pos].r) 5 { 6 v[pos].push_back(val);//val加入到v[pos]中 7 return ; 8 } 9 int mid=segTree[pos].mid(); 10 if(x <= mid) 11 Update(x,val,ls(pos)); 12 else 13 Update(x,val,rs(pos)); 14 }
例如上图b:
①-② : 10 ,调用函数Update(tid[2],10,1) ⇔ v[tid[2]].push_back(10)
①-③ : 10 ,调用函数Update(tid[3],10,1) ⇔ v[tid[3]].push_back(10)
②-④ : 10 ,调用函数Update(tid[4],10,1) ⇔ v[tid[4]].push_back(10)
③-⑤ : 10 ,调用函数Update(tid[5],10,1) ⇔ v[tid[5]].push_back(10)
线段树中的节点9中的v存储一个10
线段树中的节点5中的v存储一个10
线段树中的节点6中的v存储一个10
线段树中的节点7中的v存储一个10
这个就是Update()函数的作用;
接下来的pushUp()函数很重要:
1 void pushUp(int pos) 2 { 3 if(segTree[pos].l == segTree[pos].r) 4 return; 5 6 pushUp(ls(pos)); 7 pushUp(rs(pos)); 8 9 //将ls(pos),rs(pos)中的元素存储到pos中 10 for(int i=0;i < v[ls(pos)].size();++i) 11 v[pos].push_back(v[ls(pos)][i]); 12 for(int i=0;i < v[rs(pos)].size();++i) 13 v[pos].push_back(v[rs(pos)][i]); 14 sort(v[pos].begin(),v[pos].end());//升序排列 15 }
调用pushUp(1),将所有的pos 的 ls(pos),rs(pos) 节点信息更新到pos节点;
调用完这个函数后,你会发现:
v[1]:10,10,10,10([1,5]中的所有节点到其父节点的权值,根节点为null)
v[2]:10,10([1,3]中的所有节点到其父节点的权值)
v[3]:10,10([4,5]中的所有节点到其父节点的权值)
v[4]:10([1,2]中的所有节点到其父节点的权值)
v[5]:10([3,3]中的所有节点到其父节点的权值)
v[6]:10([4,4]中的所有节点到其父节点的权值)
v[7]:10([5,5]中的所有节点到其父节点的权值)
v[8]:null(根节点为null)
v[9]:10([2,2]中的所有节点到其父节点的权值)
你会发现,v[i]中存的值就是[ tree[i].l , tree[i].r ]中所有节点与其父节点的权值;
接下来就是询问操作了:
1 int BS(int pos,int w) 2 { 3 int l=-1,r=v[pos].size(); 4 while(r-l > 1) 5 { 6 int mid=l+((r-l)>>1); 7 if(v[pos][mid] <= w) 8 l=mid; 9 else 10 r=mid; 11 } 12 return l+1; 13 } 14 int Query(int l,int r,int pos,int w) 15 { 16 if(v[pos][0] > w)//当前区间的如果最小的值要 > w,直接返回0 17 return 0; 18 if(segTree[pos].l == l && segTree[pos].r == r) 19 return BS(pos,w);//二分查找pos区间值 <= w 得个数(还记得pushUp()中的sort函数么? 20 21 int mid=segTree[pos].mid(); 22 if(r <= mid) 23 return Query(l,r,ls(pos),w); 24 else if(l > mid) 25 return Query(l,r,rs(pos),w); 26 else 27 return Query(l,mid,ls(pos),w)+Query(mid+1,r,rs(pos),w); 28 }
AC代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ls(x) (x<<1) 4 #define rs(x) (x<<1|1) 5 #define INF 0x3f3f3f3f 6 #define mem(a,b) memset(a,b,sizeof(a)) 7 const int maxn=1e5+50; 8 9 int n,m; 10 int fa[maxn];//fa[u]:u的父节点 11 int son[maxn];//son[u]:u的重儿子 12 int dep[maxn];//dep[u]:u的深度 13 int siz[maxn];//siz[u]:以u为根的子树节点个数 14 int tid[maxn];//tid[u]:u在线段树中的位置 15 int top[maxn];//top[u]:u所在重链的祖先节点 16 int e[maxn][3];//e[i][0]与e[i][1]有条权值为e[i][2]的边 17 vector<int >v[maxn<<2];//v[i]:存储线段树中i号节点的所有边的权值 18 int num; 19 int head[maxn]; 20 struct Edge 21 { 22 int to; 23 int w; 24 int next; 25 }G[maxn<<1]; 26 void addEdge(int u,int v,int w) 27 { 28 G[num].to=v; 29 G[num].w=w; 30 G[num].next=head[u]; 31 head[u]=num++; 32 } 33 struct SegmentTree 34 { 35 int l,r; 36 int mid() 37 { 38 return l+((r-l)>>1); 39 } 40 }segTree[maxn<<2]; 41 void DFS1(int u,int f,int depth) 42 { 43 fa[u]=f; 44 son[u]=-1; 45 siz[u]=1; 46 dep[u]=depth; 47 for(int i=head[u];~i;i=G[i].next) 48 { 49 int v=G[i].to; 50 if(v == f) 51 continue; 52 DFS1(v,u,depth+1); 53 54 siz[u] += siz[v]; 55 56 if(son[u] == -1 || siz[v] > siz[son[u]]) 57 son[u]=v; 58 } 59 } 60 void DFS2(int u,int anc,int &k) 61 { 62 top[u]=anc; 63 tid[u]=++k; 64 if(son[u] == -1) 65 return ; 66 DFS2(son[u],anc,k); 67 68 for(int i=head[u];~i;i=G[i].next) 69 { 70 int v=G[i].to; 71 if(v != fa[u] && v != son[u]) 72 DFS2(v,v,k); 73 } 74 } 75 void pushUp(int pos) 76 { 77 if(segTree[pos].l == segTree[pos].r) 78 return; 79 80 pushUp(ls(pos)); 81 pushUp(rs(pos)); 82 83 //将ls(pos),rs(pos)中的元素存储到pos中 84 for(int i=0;i < v[ls(pos)].size();++i) 85 v[pos].push_back(v[ls(pos)][i]); 86 for(int i=0;i < v[rs(pos)].size();++i) 87 v[pos].push_back(v[rs(pos)][i]); 88 sort(v[pos].begin(),v[pos].end());//升序排列 89 } 90 void buildSegTree(int l,int r,int pos) 91 { 92 segTree[pos].l=l; 93 segTree[pos].r=r; 94 if(l == r) 95 return ; 96 97 int mid=l+((r-l)>>1); 98 buildSegTree(l,mid,ls(pos)); 99 buildSegTree(mid+1,r,rs(pos)); 100 } 101 //将节点x在线段树中对应的pos位置的v中加入val 102 void Update(int x,int val,int pos) 103 { 104 if(segTree[pos].l == segTree[pos].r) 105 { 106 v[pos].push_back(val);//val加入到v[pos]中 107 return ; 108 } 109 int mid=segTree[pos].mid(); 110 if(x <= mid) 111 Update(x,val,ls(pos)); 112 else 113 Update(x,val,rs(pos)); 114 } 115 int BS(int pos,int w) 116 { 117 int l=-1,r=v[pos].size(); 118 while(r-l > 1) 119 { 120 int mid=l+((r-l)>>1); 121 if(v[pos][mid] <= w) 122 l=mid; 123 else 124 r=mid; 125 } 126 return l+1; 127 } 128 int Query(int l,int r,int pos,int w) 129 { 130 if(v[pos][0] > w)//当前区间的如果最小的值要 > w,直接返回0 131 return 0; 132 if(segTree[pos].l == l && segTree[pos].r == r) 133 return BS(pos,w);//二分查找pos区间值 <= w 得个数(还记得pushUp()中的sort函数么? 134 135 int mid=segTree[pos].mid(); 136 if(r <= mid) 137 return Query(l,r,ls(pos),w); 138 else if(l > mid) 139 return Query(l,r,rs(pos),w); 140 else 141 return Query(l,mid,ls(pos),w)+Query(mid+1,r,rs(pos),w); 142 } 143 int Find(int u,int v,int w)//查询节点u到节点v之间权值小于等于w得路径个数 144 { 145 int ans=0; 146 int topU=top[u]; 147 int topV=top[v]; 148 while(topU != topV) 149 { 150 if(dep[topU] > dep[topV]) 151 { 152 swap(u,v); 153 swap(topU,topV); 154 } 155 ans += Query(tid[top[v]],tid[v],1,w); 156 v=fa[topV]; 157 topV=top[v]; 158 } 159 if(u == v) 160 return ans; 161 if(dep[u] > dep[v]) 162 swap(u,v); 163 return ans+Query(tid[son[u]],tid[v],1,w); 164 } 165 void Solve() 166 { 167 DFS1(1,1,1); 168 int k=0; 169 DFS2(1,1,k); 170 171 buildSegTree(1,k,1); 172 173 for(int i=1;i < n;++i) 174 { 175 if(dep[e[i][0]] > dep[e[i][1]]) 176 swap(e[i][0],e[i][1]);//令fa[e[i][1]] = e[i][0],方便更新操作 177 Update(tid[e[i][1]],e[i][2],1);//将e[i][2]加入到tid[e[i][1]]中 178 } 179 pushUp(1);//更新线段树中所有的pos 180 181 for(int i=1;i <= m;++i) 182 { 183 int u,v,w; 184 scanf("%d%d%d",&u,&v,&w); 185 printf("%d ",Find(u,v,w)); 186 } 187 } 188 void Init() 189 { 190 num=0; 191 mem(head,-1); 192 for(int i=0;i < 4*maxn;++i) 193 v[i].clear(); 194 } 195 int main() 196 { 197 // freopen("C:\Users\hyacinthLJP\Desktop\in&&out\contest","r",stdin); 198 while(~scanf("%d%d",&n,&m)) 199 { 200 Init(); 201 for(int i=1;i < n;++i) 202 { 203 scanf("%d%d%d",e[i]+0,e[i]+1,e[i]+2); 204 addEdge(e[i][0],e[i][1],e[i][2]); 205 addEdge(e[i][1],e[i][0],e[i][2]); 206 } 207 Solve(); 208 } 209 return 0; 210 }