二项分布(Binomial Distribution)
对Bernoulli试验序列的n次序列,结局A出现的次数x的概率分布服从二项分布
- 两分类变量并非一定会服从二项分布
- 模拟伯努利试验中n次独立的重复,每次试验成功的概率为pi
特征值
- 均值(数学期望)和方差:
- 不同的值,二项式分布有着不同的形态和偏度值
- pi值越大,呈负偏度;pi值越小,呈正偏度
- 当 pi = 0.5时,分布是对称的
- 当 n * pi 与 n * (1-pi) >= 5 时,样本比例p的抽样分布趋向于正态分布
- 当 n 较大,pi不太极端时,可以采用正态近似方法计算概率分布规律
应用
- 博彩行业的规则设定
- 正常值范围的设定(例:医疗行业)
# 对二项分布概念的理解及计算

1 # 对二项分布概念的理解及计算 2 3 from scipy.stats import binom 4 5 pi = .3; n = 10 6 k = 2; m = 8 7 8 # 求成功次数为i的概率 9 pk = 0 10 for i in range(n): 11 p = binom( n, pi ).pmf( i ) 12 if i <= k: 13 pk += p 14 print( 'P(x = {0:d}) = {1:.4f}'.format( i , p )) 15 16 # 求成功小于k次的概率 17 print('-'*20) 18 p = binom( n, pi ).cdf( k ) 19 print( 'P(x <= {0:d}) = {1:.4f}'.format( k , p )) 20 print( '比较累加值:', pk) 21 22 # 求成功大于k次,小于m次的概率 23 print('-'*20) 24 p = binom( n, pi ).cdf( m ) - binom( n, pi ).cdf( k ) 25 print( 'P({0:d} < x <= {1:d}) = {2:.4f}'.format( k , m, p ))
运行结果:

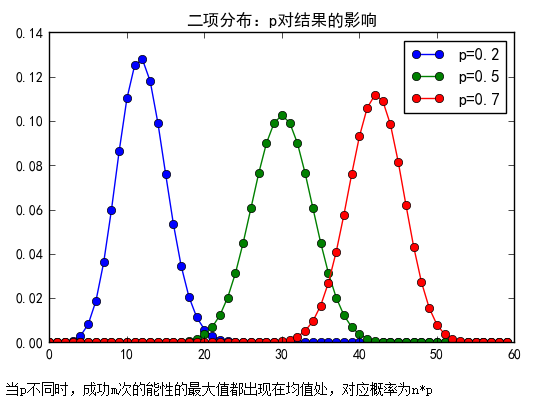
# 比较:p对结果的影响

1 import numpy as np 2 from scipy.stats import binom 3 import matplotlib.pyplot as plt 4 5 num_trials = 60 6 x = np.arange(num_trials) 7 8 plt.plot(x, binom(num_trials, 0.2).pmf(x), 'o-', label='p=0.2') 9 plt.plot(x, binom(num_trials, 0.5).pmf(x), 'o-', label='p=0.5') 10 plt.plot(x, binom(num_trials, 0.7).pmf(x), 'o-', label='p=0.7') 11 plt.legend() 12 plt.title( '二项分布:p对结果的影响' ) 13 plt.show() 14 print('当p不同时,成功m次的能性的最大值都出现在均值处,对应概率为n*p')
结果:
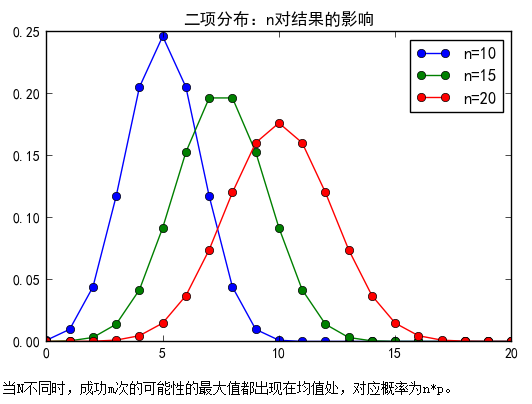
# 比较:n对结果的影响

1 import numpy as np 2 from scipy.stats import binom 3 import matplotlib.pyplot as plt 4 5 n1 = 10 6 n2 = 15 7 n3 = 20 8 p = 0.5 9 x = np.arange( max([n1,n2,n3])+1 ) 10 11 plt.plot( x, binom.pmf( x, p = 0.5, n = n1), 'o-', label='n=10') 12 plt.plot( x, binom.pmf( x, p = 0.5, n = n2), 'o-', label='n=15') 13 plt.plot( x, binom.pmf( x, p = 0.5, n = n3), 'o-', label='n=20') 14 plt.legend() 15 plt.title( '二项分布:n对结果的影响' ) 16 plt.show() 17 print('当N不同时,成功m次的可能性的最大值都出现在均值处,对应概率为n*p。')
结果: