X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。
每块金属原料的外形、尺寸完全一致,但重量不同。
金属材料被严格地堆放成金字塔形。
7
5 8
7 8 8
9 2 7 2
8 1 4 9 1
8 1 8 8 4 1
7 9 6 1 4 5 4
5 6 5 5 6 9 5 6
5 5 4 7 9 3 5 5 1
7 5 7 9 7 4 7 3 3 1
4 6 4 5 5 8 8 3 2 4 3
1 1 3 3 1 6 6 5 5 4 4 2
9 9 9 2 1 9 1 9 2 9 5 7 9
4 3 3 7 7 9 3 6 1 3 8 8 3 7
3 6 8 1 5 3 9 5 8 3 8 1 8 3 3
8 3 2 3 3 5 5 8 5 4 2 8 6 7 6 9
8 1 8 1 8 4 6 2 2 1 7 9 4 2 3 3 4
2 8 4 2 2 9 9 2 8 3 4 9 6 3 9 4 6 9
7 9 7 4 9 7 6 6 2 8 9 4 1 8 1 7 2 1 6
9 2 8 6 4 2 7 9 5 4 1 2 5 1 7 3 9 8 3 3
5 2 1 6 7 9 3 2 8 9 5 5 6 6 6 2 1 8 7 9 9
6 7 1 8 8 7 5 3 6 5 4 7 3 4 6 7 8 1 3 2 7 4
2 2 6 3 5 3 4 9 2 4 5 7 6 6 3 2 7 2 4 8 5 5 4
7 4 4 5 8 3 3 8 1 8 6 3 2 1 6 2 6 4 6 3 8 2 9 6
1 2 4 1 3 3 5 3 4 9 6 3 8 6 5 9 1 5 3 2 6 8 8 5 3
2 2 7 9 3 3 2 8 6 9 8 4 4 9 5 8 2 6 3 4 8 4 9 3 8 8
7 7 7 9 7 5 2 7 9 2 5 1 9 2 6 5 3 9 3 5 7 3 5 4 2 8 9
7 7 6 6 8 7 5 5 8 2 4 7 7 4 7 2 6 9 2 1 8 2 9 8 5 7 3 6
5 9 4 5 5 7 5 5 6 3 5 3 9 5 8 9 5 4 1 2 6 1 4 3 5 3 2 4 1
X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X
其中的数字代表金属块的重量(计量单位较大)。
最下一层的X代表30台极高精度的电子秤。
假设每块原料的重量都十分精确地平均落在下方的两个金属块上,
最后,所有的金属块的重量都严格精确地平分落在最底层的电子秤上。
电子秤的计量单位很小,所以显示的数字很大。
工作人员发现,其中读数最小的电子秤的示数为:2086458231
请你推算出:读数最大的电子秤的示数为多少?
注意:需要提交的是一个整数,不要填写任何多余的内容。
解析:
看完这道题,相信很多同学已经被吓唬了,其实这道题就是纸老虎,对于这道题,有很多解法,最具鲜明的两种做法就是
利用 双重for循环 和 递归函数解法 ,在这里,我选择后者。具体思维如下。
分析题我们可知,第 m 层的第 n 个金属承受的压力即为第 m - 1 层的第 n - 1 个 和 m - 1 层的第 n 个 金属自身的重力加上它们两个承受的压力 的和的一半(或者一半的和),而这两个金属承受的压力又会转换为它们上层的四个金属的重力加上四个金属承受压力的和的一半,以此类推,直至到达第一层,第一层的金属只有自身的重力,没有了承受的压力从而有了具体数值,退出计算,这个过程大家有没有想到一个算法,没错,就是递归算法!,获得第 m 层第 n 列 金属最终的承受的压力,如果我们把第m层第n列的金属等效于天枰,那么它承受的压力就等效与天枰的示数,从而从30个天枰的示数中找出最大值 max 最小值 min,本题的解即为 (max / min) * 2086458231;
具体代码如下:
/*本程序看似代码比网上的其他解法代码多,其实不然,因为他们的解法还需要用户手动输入每一个金属的重量,但本程序利用文件流的功能自动导入数据并利用算法智能分配给数组下标,这些都是枝枝叶叶,最重要的是递归函数的应用,这才是精髓。
因为本人为了读者便于全部理解,固将各个功能以最人性化的方式用代码解析,再加上本人算法不精深,造成计算机运算量过大从而导致会在一到两分钟才会计算出最终结果,请稍安勿躁,耐心等待。*/
#include<iostream>
#include<fstream>
#include<sstream>#include<string>
using namespace std;
#define LINES 40 //为了避免因为数组越界造成的系统自己获取的数据不为0导致
#define MINWEIGHT 2086458231 //最终结果受影响,固将行列设置为大于30,虽会对性能造成影响
//但二者权衡利弊还是这么做的好
int get_lines(int order); //得到第order个元素转换为二维数组时的行号
int get_rows(int order); //得到第order个元素转换为二维数组时的列号
//order的值是由文件流获取到数据的顺序确定的
void readdata(void); //利用文件流自动获取全部金属块的重力void data_conversion(); //为了精确度,将获取到的int数据转换为double数据
double getweight(int lines,int rows); //得到第 lines 行和第 rows 列金属块承受的压力(如果 lines = 30,则可以 //转化思想把得到的数据理解为第30列天枰的示数) 此函数为本程序的灵魂,
double getmin();
double getmax();
int data_temp[LINES][LINES]; //从文件中获取到的初始int数据
double data_temp_double[LINES][LINES]; //转换为double的数据
int main(int argc,char** argv){
double min,max;
readdata();
data_conversion();
cout << (getmax() / getmin()) * MINWEIGHT;
}
double getmin(){
double weight[29 + 1];
double min = 10000.00;
for(int i = 0;i < 29 + 1;i++){
weight[i] = getweight(29,i);
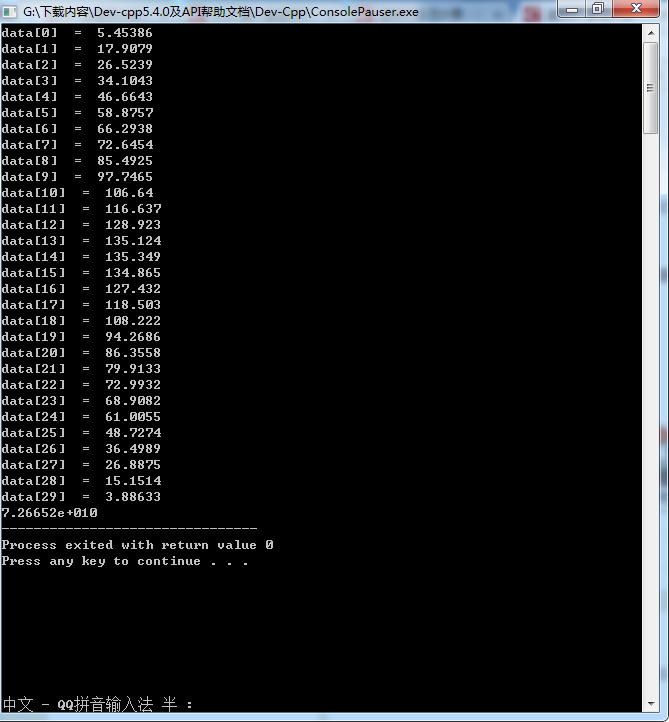
cout << "data[" << i << "] = " << weight[i] << endl;
}
for(int i = 0;i < 29 + 1;i++){
if(min > weight[i]){
min = weight[i];
}
}
return min;
}
double getmax(){
double weight[29 + 1];
double max = 0.00;
for(int i = 0;i < 29 + 1;i++){
weight[i] = getweight(29,i);
}
for(int i = 0;i < 29 + 1;i++){
if(max < weight[i]){
max = weight[i];
}
}
return max;
}
double getweight(int lines,int rows){
double weight = 0;
if(lines == 0){ //如果行数为0,则只有自身重力,不存在压力,退出递归,得到最终值
return weight;
}else{ //如果行数不为0,列数为0,则证明该金属上层左边不存在施加压力的金属
if(rows == 0){
weight = (weight + data_temp_double[lines - 1][rows] + getweight(lines - 1,rows)) / 2;
}else{ //如果行数和列数都不为0,则该金属承受的压力为上层左边和上层
//右边金属自身重力加承受压力的和的一半
weight = (weight + data_temp_double[lines - 1][rows - 1] + data_temp_double[lines - 1][rows] + getweight(lines - 1,rows - 1) + getweight(lines - 1,rows)) / 2;
}
}
return weight;
}
void data_conversion(){
double data;
for(int i = 0;i < LINES;i++){
for(int j = 0;j < LINES;j++){
stringstream ss;
ss << data_temp[i][j];
ss >> data;
data_temp_double[i][j] = data;
}
}
}
void readdata(){
ifstream fin;
fin.open("data.txt");
data_temp[LINES][LINES] = {0};
int order = 1;
while(fin){
int data = 0;
fin >> data;
data_temp[get_lines(order) - 1][get_rows(order) - 1] = data;
order++;
}
}
int get_lines(int order){
int sum = 0;
for(int i = 1;i < LINES + 2;i++){
sum = sum + i;
if(sum >= order){
return i;
}
}
}
int get_rows(int order){
int sum = 0;
for(int i = 1;i < LINES + 2;i++){
sum = sum + i;
if(sum >= order){
if(sum > order){
return get_lines(order) - (sum - order);
}else{
return i;
}
}
}
}
计算结果如下: