题目 : 等差素数列
2,3,5,7,11,13,....是素数序列。
类似:7,37,67,97,127,157 这样完全由素数组成的等差数列,叫等差素数数列。
上边的数列公差为30,长度为6。
2004年,格林与华人陶哲轩合作证明了:存在任意长度的素数等差数列。
这是数论领域一项惊人的成果!
有这一理论为基础,请你借助手中的计算机,满怀信心地搜索:
长度为10的等差素数列,其公差最小值是多少?
注意:需要提交的是一个整数,不要填写任何多余的内容和说明文字。
代码解析过程:
/*将本程序所有代码粘贴在 DEV C++ 中可直接执行*/
#include<iostream>
#include<string>
#include<fstream>
#include<windows.h>
using namespace std;
#define MAX_NUM 9591 //本人通过该程序算出10万以内的素数为9591个,固自认为该题让所求的素数列最大值在10万以内
int prime[MAX_NUM]; //如果该题给出的答案中的素数列中的最大值大于10万,则怪本人自以为是或者低估了蓝桥杯对竞赛者的要求
bool jud_prime(int value); //判断传入的参数是否为素数的函数
void savedata(); //将10万以内的素数利用文件流输入到记事本中(可不必须输出到记事本,本人为了脚踏实地确认数值是否正确).
void readdata(); //将10万以内的素数从记事本读入自定义数组中
bool isexist(int tolerance); //判断公差为传入参数的等差素数列是否存在
int get_primenums(int tolerance,int long_limit);
int array_data = 0;
void output();
int main(int argc,char** argv){
cout << " 因数据量过于庞大,计算过为复杂,再加上本人才学疏浅,算法不够精深,导致本程序会根据机器不同在一分钟不等时间内将计算结果显示出来,请各位不要着急,稍安毋躁";
system("color 1e");
savedata();
readdata();
output();
cout << endl;
return 0;
}
void savedata(){
ofstream fout;
fout.open("lanyue.txt");
int test_value = 2;
int i_temp = 0;
while(test_value != 100000){
if(jud_prime(test_value)){
prime[i_temp] = test_value;
i_temp++;
fout << test_value << " ";
}
test_value++;
}
fout.close();
}
void readdata(){
ifstream fin;
fin.open("lanyue.txt");
int sign = 0;
while(fin){
fin >> prime[sign];
sign++;
}
fin.close();
}
bool jud_prime(int value){
if(value == 2 || value == 3){
return true;
}else{
for(int i = 2;i < value;i++){
if(value % i == 0){
return false;
}else{
if(i == value - 1){
return true;
}
}
}
}
}
bool isexist(int tolerance){ //判断10万以内的素数中是否存在公差为tolerance的等差素数列
int jud_nums = 0;
int data_temp = 0;
for(int i = 0;i < MAX_NUM;i++){
int nums = 0;
data_temp = prime[i];
for(int j = i + 1;j < MAX_NUM;j++){
if(data_temp + tolerance == prime[j]){
nums++;
data_temp = prime[j];
if(nums >= 2){
return true;
}
}
}
}
return false;
}
int get_primenums(int tolerance,int long_limit){ //将10万以内的等差素数中公差为tolerance,项数大于long_limit的等差素数列显示出来
int data_temp = 0;
int nums = 1;
array_data = long_limit;
int array_[array_data];
for(int i = 0;i < MAX_NUM;i++){
data_temp = prime[i];
nums = 1;
for(int j = i + 1;j < MAX_NUM;j++){
if(data_temp + tolerance == prime[j]){
array_[nums - 1] = data_temp;
if(nums == array_data - 1){
array_[nums] = prime[j];
}
nums++;
data_temp = prime[j];
}
if(j == MAX_NUM - 1 && nums == long_limit){ //判断如果循环到10万以内最大的素数并且该数列的项数大于您传入参数时,将该数列显示出来。
cout << endl << endl << "公差为 " << tolerance << " 的等差素数列在 " << "0 - " << 100000 << " 以内共有 " << nums << " 项" << endl;
for(int i = 0;i < array_data;i++){
cout << array_[i] << " ";
}
}
}
}
}
void output(){
Sleep(5000);
system("cls");
for(int i = 1;i < 500;i++){ //可以自己更改i的值来改变等差素数列的最大公差
if(isexist(i)){
get_primenums(i,10); //get_primenums(int data1,int data2)中第一个参数用来控制等差数据的公差,第二个参数用来控制等差数列的项数。
}
}
}
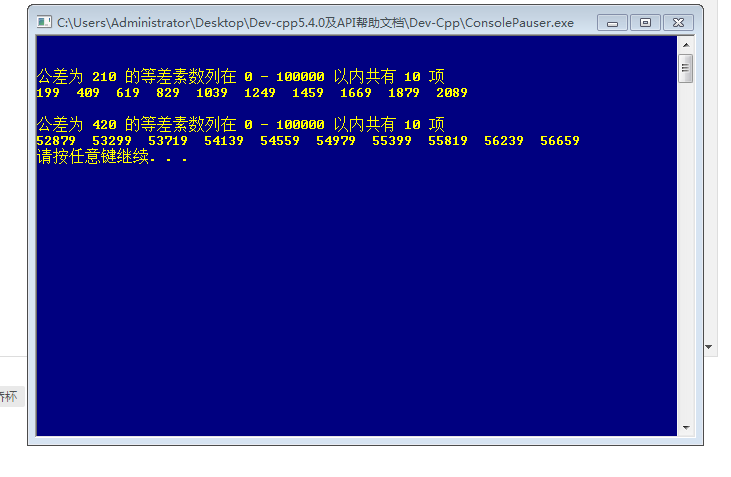
计算结果如下:
从图中可以看出10万以内的项数为10的等差素数列有两个,其中最小公差为210.