什么是贝塞尔曲线?
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。
来源
贝塞尔曲线于1962,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发,以稳定数值的方法求出贝兹曲线。
贝塞尔曲线完全由其控制点决定其形状, n个控制点对应着n-1阶的贝塞尔曲线,并且可以通过递归的方式来绘制.
特点
贝塞尔曲线形状完全由控制点控制,有n个控制点就对应n-1阶的贝塞尔曲线。
Tip:下面公式中,B指曲线中点的集合,P指点,t指变化时间
线性公式:
给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。这条线由下式给出: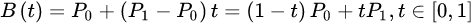
且其等同于线性插值。
二次方公式
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪: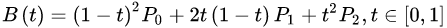
TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。
三次方公式
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
曲线的参数形式为: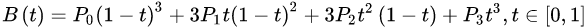
现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝兹样条组成的三次贝兹曲线,用来描绘曲线轮廓。
一般参数公式
阶贝兹曲线可如下推断。给定点P0、P1、…、Pn,其贝兹曲线即: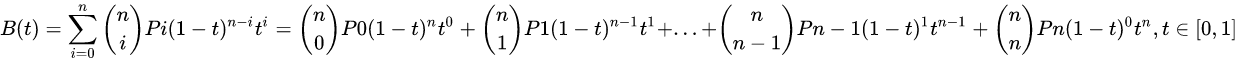
如上公式可如下递归表达: 用表示由点P0、P1、…、Pn所决定的贝兹曲线。
用平常话来说,阶的贝兹曲线,即双阶贝兹曲线之间的插值。