1. 为什么要归一化?
表示一个事物有不同的维度{即:属性},每个属性的取值范围不同,导致计算时此属性占用的权重不同,即数据的量纲不同,量纲小的数据容易受到量纲大的数据影响。
如:
| 属性 | A-person | B-persion |
| 身高 | 1.75 | 1.81 |
| 年龄 | 41 | 26 |
| 收入 | 40000 | 10000 |
计算两个人的差异:
diff = (A.身高-B.身高)2 + (A.年龄-B.年龄)2 + (A.收入-B.收入)2
= (1.75-1.81)2 + (41-26)2 + (40000-10000)2
= 0.0036 + 225 + 900000000
距离 = diff1/2 = 30000.00375
问题来了,看这些属性,发现收入占用的权重太高,身高和年龄占用的权重相对较低,怎么弱化收入占用的权重呢?
我们把身高,年龄和收入这些属性映射到一个单位区间(0,1)中。
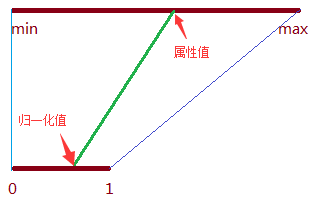
图中,根据梯形的特点可以得到如下公式
(1 - 0) / (max - min) = (归一化值 - 0) / (属性值 - min)
所以,归一化值 = (属性值 - min) / (max - min)
备注:
这种方法的优点是:可以把数据压缩到0-1空间内,但是对量纲大的数据压缩比例比较大。
假如3个属性最大和最小值如下:
| 属性 | 最大值 | 最小值 |
| 身高 | 1.2 | 2.1 |
| 年龄 | 101 | 16 |
| 收入 | 100000 | 500 |
经过归一化操作后:
| A-person | B-person | |
| 身高归一化值 |
= (1.75-1.2)/(2.1-1.2) = 0.55 / 0.9 = 0.61 |
= (1.81-1.2)/(2.1-1.2) = 0.61 / 0.9 = 0.678 |
| 年龄归一化值 |
= (41-16)/(101-16) = 25 / 85 = 0.294 |
= (26-16)/(101-16) = 20 / 85 = 0.235 |
| 收入归一化值 |
= (40000-500)/(100000-500) = 39500 / 99500 = 0.397 |
= (10000-500)/(100000-500) = 19500 / 99500 = 0.196 |
使用归一化值计算两个人的差异:
diff = (A.身高归一化值-B.身高归一化值)2 + (A.年龄归一化值-B.年龄归一化值)2 + (A.收入归一化值-B.收入归一化值)2
= (0.61-0.678)2 + (0.294-0.235)2 + (0.397-0.196)2
= 0.004624 + 0.003481 + 0.040401
计算的值可以看出,3个属性占用的权重在一个数量级上,每个属性都不会独大。
距离 = diff1/2 = 0.2202