一、导数
# 参考百科:导数
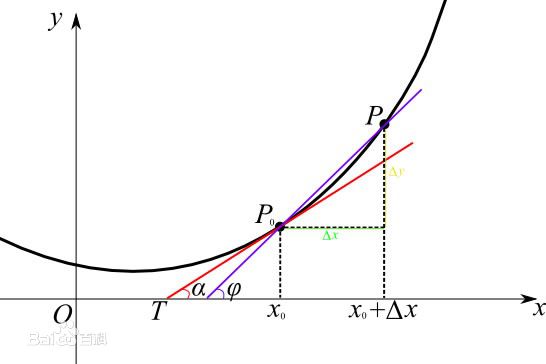
- 定义:当函数 y = f(x) 的自变量x在一点 x0 上产生一个增量 Δx 时,函数输出值的增量 Δy 与自变量增量 Δx 的比值在 Δx 趋于 0 时的极限 a 如果存在,a 即为在 x0 处的导数,记作 f'(x0) 或 df(x0) / dx;
- 一个函数在某一点的导数描述了这个函数在这一点附近的变化率;
- 公式:
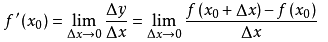
- 常见函数的求导公式:
| 函数 | 原函数 | 导函数 |
|---|---|---|
|
(即常数)
|
|
|
| 指数函数 |
|
|
| 幂函数 |
|
|
| 对数函数 |
|
|
| 正弦函数 |
|
|
| 余弦函数 |
|
|
| 正切函数 |
|
|
| 余切函数 |
|
|
| 正割函数 |
|
|
| 余割函数 |
|
|
| 反正弦函数 |
|
|
| 反余弦函数 |
|
|
| 反正切函数 |
|
|
| 反余切函数 |
|
|
|
|
|