问题描述
https://leetcode.com/problems/longest-palindromic-subsequence/description/
一个例子:
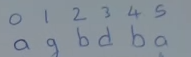
令数组为a,画一个行列为a长度的矩阵,令为T
首先看长度等于1的情况:
也就是只看一个元素,比如只看a[0]这个元素,也就是一个a,显然最长回文序列是1。只看a[1],即g,显然最长回文序列为1。其实也就是
T[i][j] (i==j)的元素位置全置为1。
看长度为2的情况:
先看a[0~1],也就是a,g。
- 先看a和g是否相等,相等则在各自长度为1的情况下的最长回文序列的前提上加2,
- 否则划分成子问题,看成长度为1的a,和长度为1的g,之前得出的矩阵中(T[0][0]和T[1][1])可以看出分别为1 ,1.
- 条件2符合,因此取T[0][0]和T[1][1]中较大值,即1
由以上两个考虑得出a,g最长回文序列为T[0][1]=1.
在看a[1~2],也就是g,b。
- 先看g和b是否相等,相等则在各自长度为1的情况下的最长回文序列的前提上加2,
- 否则划分成子问题,看成长度为1的g,和长度为1的b,之前得出的矩阵中(T[1,1]和T[2][2])可以看出分别为1 ,1.
- 条件2符合,因此取T[0][0]和T[1][1]中较大值,即1
......
看长度为3的情况:
先看a[0~2],也就是a g b。
- 先看a和b是否相等,相等则在各自长度为2的情况下的最长回文序列的前提上加2,
- 否则划分成子问题,看成长度为2的a g(T[0][1]=1),和长度为2的g b,(其T[1][2]=1),之前得出的矩阵中(T[0][1]和T[1][2])可以看出分别为1 ,1.
- 条件2符合,因此取T[0][0]和T[1][1]中较大值,即1
在看a[1~3],需要填充的是T[1][3]的值,也就是g b d。
- 先看g和b是否相等,相等则在各自长度为2的情况下的最长回文序列的前提上加2,
- 否则划分成子问题,看成长度为2的g b(T[1][2]=1),和长度为2的g b,(其T[2][3]=1),之前得出的矩阵中(T[1][2]]和T[2][3])可以看出分别为1 ,1.
- 条件2符合,因此取T[0][0]和T[1][1]中较大值,即T[1][3]=1
再看a[2~4],需要填充的是T[2][4]的值,也就是b d b。
- 先看b和b是否相等,相等则在各自长度为2的情况下的最长回文序列的前提上加2,
- 否则划分成子问题,看成长度为2的b d(T[2][3]=1),和长度为2的d b,(其T[3][4]=1),之前得出的矩阵中(T[1][2]]和T[2][3])可以看出分别为1 ,1.
- 条件1是符合的,因此取T[i+1][j-1]的值(也就是T[3][3])+2,即T[2][4]=3
看一下图示:
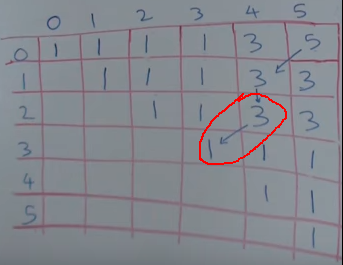
重复上述步骤即可
上述步骤用代码描述如下:

结果图:
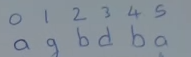

如果要输出回文序列,则可以看这样的箭头指,由那个指向线,可以看出:
从0 5 (T[0][5])开始 即 a a。
然后左下角的3是从正下方的3来的,即 2 4(T[2][4])来的 即a b b a。
然后3又是从1来的,即3 3 (T[3][3])也就是 d。
得到最长回文序列如下。
a b d b a
参考:
https://blog.csdn.net/xiaocong1990/article/details/54976319
https://www.youtube.com/watch?v=_nCsPn7_OgI&list=PLrmLmBdmIlpsHaNTPP_jHHDx_os9ItYXr&index=9