关于问题求解,书中有一个实际的案例。
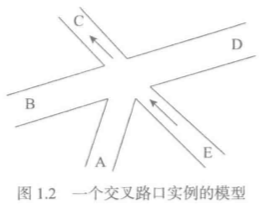
上图是一个交叉路口的模型,现在问题是,怎么安排红绿灯才可以保证相应的行驶路线互不交错。
第一步,就是把问题弄清楚。
怎么能让每一条行驶路线不冲突呢?
其实,就是给所有的行驶路线分组(这样保证了安全问题,不会撞车)。
并且,所做的分组应该尽可能大一些,用以提高路口的通行效率(经济问题,如果一个组一条路线,虽然不会撞车,但是等待的时间会很长)。
有了上面的最大化分组的想法。那么就进一步将问题具体化。
这个路口有13个可供行驶的方向:AB,AC,AD,BA,BC,BD,DA,DB,DC,EA,EB,EC,ED。
现在问题就转化为,给这13条路线分组,使其各个组不冲突,并且最大化组中的成员。
在书中引出了一个冲突图,用来表示各个路线的冲突。
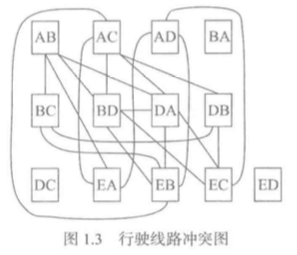
其中图中元素称之为顶点,连线称之为边或者弧。相互之间有边的顶点称为邻接顶点。
安全分组就变成了另外一种说法,为冲突图中的顶点确定一种分组,保证属于同一分组的所有顶点互不邻接。
到了这里就完了第一步,将问题严格化。
第二步,就是进行数据结构与算法设计
使用什么样的数据结构来表示冲突中的形式路线,又用哪种算法来计算分组。
书中首先提到了一个最佳着色算法,其实就是著名的四色问题,这个算法能找到最佳的分组方案。但是由于算法代价太高,效率不高。因此着重介绍了一个更为简单的算法。
那就是贪心法。它的基本想法是这样的:利用当时掌握的信息,尽可能地向得到解的方向前进,知道不能继续再换一个方法。
那么在这个例子中的具体表现就是:就是确定一个分组,这个分组里的成员互相都不邻接,也就是说不能冲突。当这个分组完成之后,再确定下一个分组。
按照这个方法,上面的例子分组就是:
{AB,AC,AD,BA,DC,ED}
{BC,BD,EA}
{DA,DB}
{EB,EC}
算法的伪代码如下:
输入:图G #记录着图中顶点连接的关系
集合verts保存G中所有的顶点 #建立初始状态
设置集合groups为空集 #记录得到的分组,元素是顶点集合
while 存在未着色顶点:
选一种新的颜色
在未着色顶点中给尽量多的无连边的点着色(构建一个分组)
记录新着色的顶点组
python伪代码:
new_group = 空集
for v in verts:
if v 与new_group集合中的顶点都不相连:
将v从verts中取出
new_group.add(v)
循环结束时,new_grouo是可以用一种新的颜色着色的顶点集合
第三步,编写代码。
其实,上面的伪代码已经接近于具体程序了。只是还有一些细节需要考虑。
1、如何表示颜色。这个简单,用整数就可以。其实,用不用颜色表示都可以,只要将每个分组分开即可。这里采用二元组来表示,一个表示颜色,一个表示分好的组。、
2、如何记录分组。可以用一个集合来记录,也就是groups是集合的集合。
3、如何表示图结构?这个比较难,是后面的内容,这里先略过。
由此可得出python的代码:
def coloring(G)
color = 0
groups = set()
verts = vertices(G) #用来获取所有的顶点
while verts:
new_groups = set()
for v in list(verts):
if not_adjacent_with_set(v, newgroup, G):
new_group.add(v)
verts.remove(v)
groups.add((color, new_group))
color += 1
return grous
第四步,测试代码,寻找一些边界例子测试代码的严谨性以及逻辑性。
由于,这里并不是一个完整的项目,而且这个例子比较简单,就简单分析讨论一下,应该注意的几个问题。
1、它的解唯一吗?
其实,大致观察一下,就会发现,上面的算法只能给出一个恰好的解。例如,下面的分组也是一个解
{AB,EB,EC}
{AC,AD,BC,}
{BA,BD,DB,ED}
{DA,DC,EA}
其实,经过分析。对于BA、DC、ED三个顶点,将它们放在任何一个分组都是可以的。因为它们不跟任何一个顶点相连,也就是公认的无害右转弯。对于这个设计具体得看对于冲突概念的定义。
2、再次回顾一下算法的实现跟原来的问题是否相符
原来的问题是怎么分配,各个路线才能不冲突。
而上面的算法给出了一种不冲突的方法,但并不是最优的解。比如:上面的算法中每个分组都顶点都不允许重复,也就是各个分组互不相交。但真正的问题并没有这个要求。无害的右转弯就与各个分组都不冲突,完全可以都分配在各个分组里面。使其得到下面的分配:
{AB,AC,AD,BA,DC,ED}
{BC,BD,EA,BA,DC,ED}
{DA,DB,BA,DC,ED}
{EB,EC,BA,DC,ED}
这样就会将分组尽可能地扩充,使其经济效率更高(这个分组还可以继续扩充为{DA,DB,BA,DC,ED,AD})。
当然,这个问题还会有其他的一些具体的问题,这里就不讨论了。作者主要是用一个例子来带我们分析了一下,如何将生活中的实际问题,一步一步通过分析设计,最终得到一个完整的正确的效率高的计算机程序。