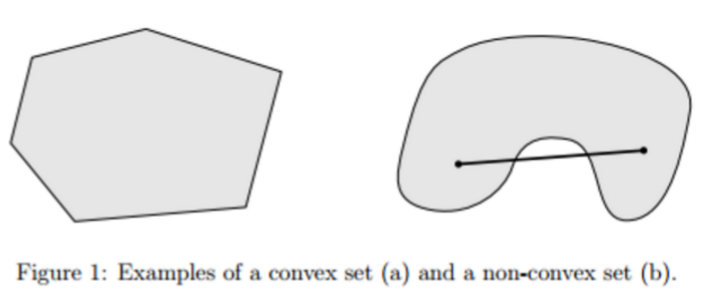
一、凸集
定义:给定一个集合C⊆RnC⊆Rn,满足下列条件则称为凸集
x,y∈C⇒tx+(1−t)y∈Cx,y∈C⇒tx+(1−t)y∈C 对于任意的 0≤t≤1
凸集:如果集合A中任意两个元素的连线上的点也在集合内,则为凸集
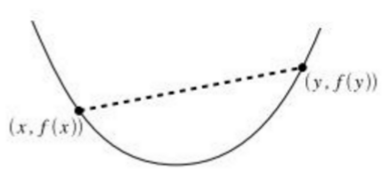
二、凸函数
定义:给定映射f:Rn→Rf:Rn→R 并且 dom(f)⊆Rn(f)⊆Rn为凸集,那么
f(tx+(1−t)y)≤tf(x)+(1−t)f(y)f(tx+(1−t)y)≤tf(x)+(1−t)f(y) 对于任意 0≤t≤10≤t≤1,且 任意x,y∈dom(f)x,y∈dom(f)。
凸函数:函数任意两点连线上的值大于对应对应自变量出的函数值,则为凸函数
三、凸优化
凸优化问题有一个重要的结论:凸优化问题的局部最优解,就是全局最优解。