最近测试有一道这样的题目,由于我以前看过怎么做,但是又不确定,所以就把做法的正确性证明了之后再做的。结果还是写挂了,只对了一个点。
算法
对于每个点,以它为中心把平面分成八个,每个面里面找一个距离它最近的点连一条边,然后做最小生成树即可。
为什么这样是对的呢?
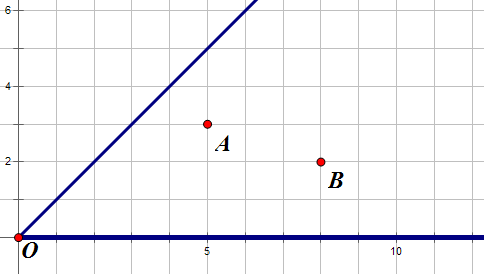
如图,对于点(O)的其中一个平面,假设点(A)是离它最近的点,(B)点不是最近的点,我们可以证明,最小生成树里面可以不要(OB)这条边。假设有(OB)这条边,我们完全可以用(OA+AB)来代替,而且答案不会差。注意,这里是曼哈顿距离,所以(OA+AB leq OB),取到等号是的图如下:
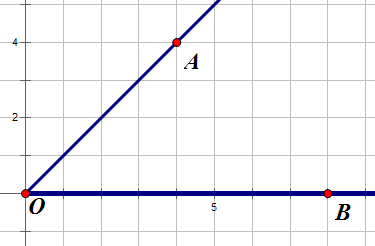
然后我们就可以各种搞了,我们可以写离散化的树状数组或者是动态开结点的线段树,我偏向于后者,因为思维复杂度小,尽管可能会慢一点(经测,是树状数组的2.2倍)。
好吧,我错了。离散化其实更好搞,我们可以先把所以可能的坐标存进一个数组,用的时候lower_bound就可以定位了,比线段树爽多了。
简要代码
struct Node {
Node* s[2];
pair<int, int> key;
void update() {
key = make_pair(INF, -1);
if (s[0]) tension(key, s[0]->key);
if (s[1]) tension(key, s[1]->key);
}
};
Node mem[MAXN * LOGUPPER];
Node* curMem;
bool cmp(const Point &a, const Point &b) {
if (a.first.second != b.first.second)
return a.first.second > b.first.second;
//return a.second > b.second;
return a.first.first > b.first.first;
}
void modify(Node* &idx, int L, int R, int x, pair<int, int> val) {
if (idx == NULL) {
idx = curMem ++;
//idx = new Node;
idx->s[0] = idx->s[1] = NULL;
idx->update();
}
if (L == R) {
tension(idx->key, val);
}
else {
int M = (L + R) >> 1;
if (x <= M) modify(idx->s[0], L, M, x, val);
else modify(idx->s[1], M + 1, R, x, val);
idx->update();
}
}
pair<int, int> query(Node* &idx, int L, int R, int x, int y) {
if (idx == NULL) return make_pair(INF, -1);
if (x <= L && y >= R) return idx->key;
int M = (L + R) >> 1;
pair<int, int> ret = make_pair(INF, -1);
if (x <= M) tension(ret, query(idx->s[0], L, M, x, y));
if (y > M) tension(ret, query(idx->s[1], M + 1, R, x, y));
return ret;
}
void build() {
sort(A + 1, A + 1 + n, cmp);
curMem = mem;
Node* root = NULL;
for (int i = 1; i <= n; i ++) {
int tmp = A[i].first.first - A[i].first.second;
pair<int, int> result = query(root, -UPPER, UPPER, tmp, UPPER);
int tmp2 = A[i].first.first + A[i].first.second;
if (result.second != -1)
Graph::getOneEdge(result.second, A[i].second, result.first - tmp2);
modify(root, -UPPER, UPPER, tmp, make_pair(tmp2, A[i].second));
}
}
int main() {
freopen("travel.in", "r", stdin);
freopen("travel.out", "w", stdout);
scanf("%d", &n);
bool test56 = true;
for (int i = 1; i <= n; i ++) {
scanf("%d%d", &A[i].first.first, &A[i].first.second);
A[i].first.first -= UPPER >> 1;
A[i].first.second -= UPPER >> 1;
if (A[i].first.first != 1) test56 = false;
A[i].second = i;
}
{
for (int i = 0; i < 2; i ++) {
for (int j = 0; j < 2; j ++) {
build();
for (int i = 1; i <= n; i ++)
swap(A[i].first.first, A[i].first.second);
}
for (int i = 1; i <= n; i ++) {
Point tmp = A[i];
A[i].first.first = tmp.first.second;
A[i].first.second = - tmp.first.first;
}
}
}