前言
抽样方法
-
简单随机抽样:抽签法和随机数表法
-
系统抽样
-
分层抽样
-
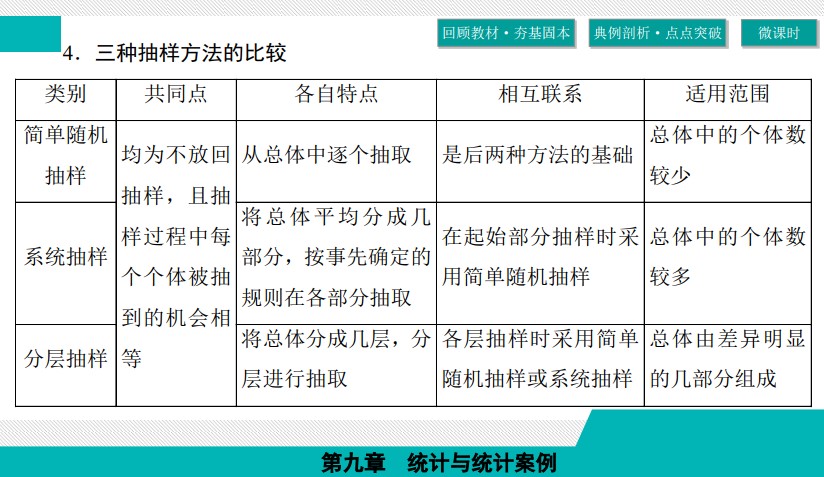
三种抽样方法的区别和联系
运算技巧
- (A,B,C)三种不同型号的产品,数量比为(3:4:7),分层抽样抽出容量为(n)的样本,样本中(A)产品有(15)件,求样本容量(n)。
法1:(cfrac{3}{3+4+7} imes n=15),解得(n=70);
法2:引入比例因子,三种产品的数量分别为(3k,4k,7k),则(3k=15),即(k=5),
故样本容量为(n=3k+4k+7k=14k=14 imes 5=70);
- 利用随机数表法时,由于每一位上的数字都是随机等可能出现的,故读数的方向可以向左、向右,也可以向上、向下,甚至斜向读数都可以,一般从左向右读数。

典例剖析
①采用随机抽样法,将零件编号为(00),(01),(cdots),(99),抽出20个;
②采用系统抽样法,将所有零件分成(20)组,每组(5)个,然后每组中随机抽取一个;
③采用分层抽样法,随机从一级品中抽取(4)个,二级品中抽取(6)个,三级品中抽取(10)个,则【 】
(A.)不论采用哪种抽样方法,这(100)个零件中每个被抽到的概率都是(cfrac{1}{5})
(B.)①②两种抽样方法,这(100)个零件中每个被抽到的概率都是(cfrac{1}{5}),③并非如此
(C.)①③两种抽样方法,这(100)个零件中每个被抽到的概率都是(cfrac{1}{5}),②并非如此
(D.)采用不同的抽样方法,这(100)个零件中每个被抽到的概率各不相同
分析:根据三种抽样的定义,简单随机抽样、系统抽样、分层抽样都是随机抽样,每个个体被抽到的概率都相等,都是等概率抽样。故选(A)。
解后反思:
-
总体容量为(N),样本容量为(n),不论哪一种抽样方法,在整个抽样过程中,每一个个体被抽到的概率都为(cfrac{n}{N});
-
原理:总体容量为(N),样本容量为(n),求个体(a)被抽到的概率。
分析:从(N)个任意抽取(n)个的所有可能为(C_N^n)种,其中抽到个体(a)的可能为(C_1^1cdot C_{N-1}^{n-1})种,
故个体(a)被抽到的概率为(P=cfrac{C_1^1cdot C_{N-1}^{n-1}}{C_N^n}=cfrac{A_{N-1}^{N-1}/A_{n-1}^{n-1}}{A_N^N/A_n^n}=cfrac{A_{N-1}^{N-1}cdot A_n^n}{A_N^Ncdot A_{n-1}^{n-1}}=cfrac{n}{N})。
- 总体容量为(362),样本容量为(40),再采用系统抽样方法抽取,此时需要先剔除(2)个个体,则此时每一个个体如(A),被抽到的概率还是(cfrac{40}{362});
分析:个体(A)被抽到,需要第一次抽取时未被剔除,其概率为(cfrac{360}{362});而第二次个体(A)必须被抽到,其概率为(cfrac{40}{360}),故个体(A)被抽到的概率为(cfrac{40}{362}).
分析:系统抽样得到的样本编号成等差数列,令(a_1=7), (a_2=32),(d=25),所以(a_n=7+25(n-1)leq 500),所以(nleq 20),最大编号为(7+25 imes 19=482)。
分析:总体容量为(6+12+18=36),
当样本容量是(n),由题意可知,系统抽样的间隔为(cfrac{36}{n}),
分层抽样的比例是(cfrac{n}{36}),抽取的工程师人数为(cfrac{n}{36} imes 6=cfrac{n}{6}),
抽取的技术员人数为(cfrac{n}{36} imes 12=cfrac{n}{3}),抽取的技工人数为(cfrac{n}{36} imes 18=cfrac{n}{2}),
所以(n)应该是(6)的倍数,(36)的约数,即(n=6,12,18),
当样本容量为((n+1))时,总体容量是(35)人,系统抽样的间隔为(cfrac{35}{n+1}),
由于(cfrac{35}{n+1})必须是整数,所以(n)只能取(6),即样本容量为(n=6)。

