前言
题目原貌
(1). (A_0),(A_1),(A_2),(cdots),(A_8), 所有规格的纸张的幅宽(以 (x) 表示)和长度(以 (y) 表示 ) 的比例关系都为(x:y=1:sqrt{2});
(2).将 (A_0) 纸张沿长度方向对开成两等分,便成为 (A_1) 规格,(A_1) 纸张沿长度方向对开成两等分,便成为 (A_2) 规格, (cdots), 如此对开至 (A_8) 规格。
现有 (A_0)、(A_1)、(A_2)、(cdots),(A_8) 纸各一张, 若 (A_4) 纸的宽度为(2 dm), 则 (A_0) 纸的面积为 ____________ (dm^{2}); 这 (9) 张纸的面积之和等于 ____________ (dm^{2});
初步解析
结合题目,我们做个示意图,大致得到如下信息,
① 每个规格的纸张的长度是宽度的 (sqrt{2}) 倍,
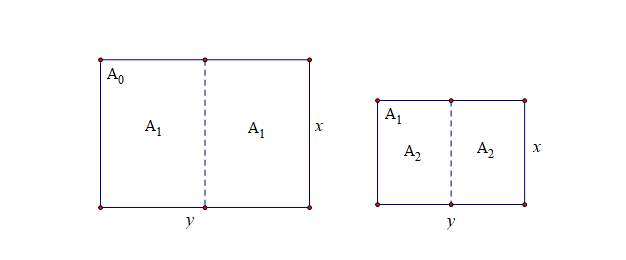
② (A_0) 能被等分为两个 (A_1),同理,(A_1) 能被等分为两个 (A_2),等等,
③ (A_0) 的宽度是 (A_1) 的长度,(A_1) 的宽度是 (A_2) 的长度,等等,
④ (A) 系列的纸张的长度能构成等比数列,(A) 系列的纸张的宽度能构成等比数列,
抽象概括
为便于表述,我们需要定义各个幅面规格,原本是 (A_0)、(A_1)、(A_2)、(cdots),(A_8) 共 (9) 个,
需要将其高度抽象概括,糅合为一句话,可以引入动态下标,比如不妨定义为 (A_{i}) ((i=0,1,2,cdots,8)),
同时需要定义各个规格 (A_{i}) 的长度和宽度,由于每一种规格都有长度和宽度,故要注意对应性,
(A_{i}) ((i=0,1,2,cdots,8))的纸张的长度为(a_{i+1})[注意,一则数列中没有(a_0),故使用(a_{i+1});二则此处还暗含了函数关系,比如当你认可了(A_{i}) 纸张的长度为(a_{i+1})后,则(A_{i+1}) 纸张的长度为(a_{i+2}),(A_{i+2}) 纸张的长度为(a_{i+3}),等等如此,],面积为(S_{i+1})[注意事项同于前边],
接下来,要寻找其中的等量关系,以便于找到解题的突破口和题目的模型,
注意到,(A_{i+1}) 的长度和 (A_{i}) 的宽度相等,故相等关系有了,只要分别表达即可。
到此,我们基本能确定,应该依托等比数列的模型来求解即可;
整合解析
解析:可设幅面规格为 (A_{i}) ((i=0,1,2,cdots,8))的纸张的长度为(a_{i+1}),面积为(S_{i+1}),
(A_{i}) 的宽度为 (cfrac{sqrt{2}}{2}a_{i+1}), (A_{i+1}) 的长度和 (A_{i}) 的宽度相等,
(A_{i+1}) 的长度为 (a_{i+2}=cfrac{sqrt{2}}{2} a_{i+1}), 即(cfrac{a_{i+2}}{a_{i+1}}=cfrac{sqrt{2}}{2}),
故数列 ({a_n})是以 (cfrac{sqrt{2}}{2}) 为公比的等比数列,
由题意可知,(A_{4})纸的宽度为(cfrac{sqrt{2}}{2}a_{5}=2), 故 (a_{5}=2sqrt{2}),
则(a_{1}=cfrac{a_{5}}{(cfrac{sqrt{2}}{2})^{4}}=cfrac{2 sqrt{2}}{cfrac{1}{4}}=8sqrt{2}),
(A_0) 纸的面积为 (S_{1}=) 长 ( imes) 宽 (=cfrac{sqrt{2}}{2}a_{1}^{2}=cfrac{sqrt{2}}{2} imes(8sqrt{2})^{2}=64sqrt{2}) ((dm^{2}))
又 (S_{1}=cfrac{sqrt{2}}{2}a_{1}^{2}),(S_{2}=cfrac{sqrt{2}}{2}a_{2}^{2}),(cdots),则(S_{n}=cfrac{sqrt{2}}{2}a_{n}^{2}),
则(cfrac{S_{n+1}}{S_{n}}=cfrac{cfrac{sqrt{2}}{2}a_{n+1}^{2}}{cfrac{sqrt{2}}{2}a_{n}^{2}}=(cfrac{a_{n+1}}{a_n})^2=(cfrac{sqrt{2}}{2})^2=cfrac{1}{2}),
故数列 ({S_n}) 是以 (64sqrt{2}) 为首项,以(cfrac{1}{2})为公比的等比数列,
因此,这 (9) 张纸的面积之和为(sumlimits_{i=1}^9S_{i})(=cfrac{64sqrt{2} imes(1-cfrac{1}{2^{9}})}{1-cfrac{1}{2}}=cfrac{511sqrt{2}}{4}) ((dm^{2}))