借助比例因子简化运算

前言

涉及到比例的相关运算，如果能引入比例因子，可能会使得计算变得很简单，主要原因是整式的运算相比分式的运算要简单且不容易出错。尤其是涉及到连比的形式，更是如此。

相关素材

• 常用的勾股数：(3n，4n，5n(nin N^*))；(5，12，13)；(7，24，25)；(8，15，17)；(9，40，41)；

• 连比形式或比例形式，可以引入非零比例因子简化运算，这样的运算可能在解三角形中，圆锥曲线的运算，等比数列的相关运算中。^[1]

典例剖析

例1【2017全国卷1理科第11题】已知(2^x=3^y=5^z)，比较(2x、3y、5z)的大小；

分析：令(2^x=3^y=5^z=k)，则(x=log_2k=cfrac{lgk}{lg2})，(y=log_3k=cfrac{lgk}{lg3})，(z=log_5k=cfrac{lgk}{lg5})，

故(2x=cfrac{2lgk}{lg2}=cfrac{lgk}{cfrac{1}{2}lg2}=cfrac{lgk}{lgsqrt{2}})，

(3y=cfrac{3lgk}{lg3}=cfrac{lgk}{cfrac{1}{3}lg3}=cfrac{lgk}{lgsqrt[3]{3}})，

(5z=cfrac{5lgk}{lg5}=cfrac{lgk}{cfrac{1}{5}lg5}=cfrac{lgk}{lgsqrt[5]{5}})，接下来，

法1：(单调性法)转化为只需要比较(sqrt[2]{2})，(sqrt[3]{3})，(sqrt[5]{5})三者的大小即可。

先比较(sqrt[2]{2})，(sqrt[3]{3})，给两个式子同时6次方，

得到((sqrt[2]{2})^6=2^3=8)，((sqrt[3]{3})^6=3^2=9)，

故(sqrt[2]{2}<sqrt[3]{3})，则(cfrac{lgk}{lgsqrt[2]{2}}>cfrac{lgk}{lgsqrt[3]{3}})，

即得到(2x>3y)

再比较(sqrt[2]{2})，(sqrt[5]{5})，给两个式子同时10次方，

得到((sqrt[2]{2})^{10}=2^5=32)，((sqrt[5]{5})^{10}=5^2=25)，

故(sqrt[2]{2}>sqrt[5]{5})，则(cfrac{lgk}{lgsqrt[2]{2}}<cfrac{lgk}{lgsqrt[3]{3}})，

即得到(5z>2x)，综上得到(3y<2x<5z)

法2：(作差法)

(2x-3y=cfrac{2lgt}{lg2}-cfrac{3lgt}{lg3}=cfrac{lgt(2lg3-3lg3)}{lg2lg3}=cfrac{lgt(lg9-lg8)}{lg2lg3}>0)，故(2x>3y);

(2x-5z=cfrac{2lgt}{lg2}-cfrac{5lgt}{lg5}=cfrac{lgt(2lg5-5lg2)}{lg2lg5}=cfrac{lgt(lg25-lg32)}{lg2lg5}<0)，故(2x<5z);

综上有(3y<2x<5z)。

法3：(作商法)

(cfrac{2x}{3y}=cfrac{2}{3}cdot cfrac{lg3}{lg2}=cfrac{lg9}{lg8}=log_89>1)，故(2x>3y)；

(cfrac{5z}{2x}=cfrac{5}{2}cdot cfrac{lg2}{lg5}=cfrac{lg2^5}{lg5^2}=log_{25}32>1)，

故(5z>2x)；故(3y<2x<5z)。素材链接

例2已知(a，b>0)，且满足(2+log_2a=3+log_3b=log_6(a+b))，求(cfrac{1}{a}+cfrac{1}{b})的值；

分析：引入正数因子(k)，

令(2+log_2a=3+log_3b=log_6(a+b)=k(k>0))，

则由(2+log_2a=log_2(4a)=k)，

得到(4a=2^k)，即(a=cfrac{2^k}{2^2}=2^{k-2})；

由(3+log_3b=log_3(27b)=k)，

得到(27b=3^k)，即(b=cfrac{3^k}{3^3}=3^{k-3})；

由(log_6(a+b)=k)，

得到(a+b=6^k)；

则(cfrac{1}{a}+cfrac{1}{b}=cfrac{a+b}{ab}=cfrac{6^k}{2^{k-2}cdot 3^{k-3}}=cfrac{2^kcdot 3^k}{2^kcdot 2^{-2}cdot 3^kcdot 3^{-3}})

(=cfrac{1}{2^{-2}cdot 3^{-3}}=2^2cdot 3^3=108)

例3已知(2^x=3^y)，求(cfrac{x}{y})的值。

分析：令(2^x=3^y=k)，则(x=log_2k=cfrac{1}{log_k2})，(y=log_3k=cfrac{1}{log_k3})，

故(cfrac{x}{y}=cfrac{frac{1}{log_k2}}{frac{1}{log_k3}}=cfrac{log_k3}{log_k2}=log_23=cfrac{lg3}{lg2})。

例4【2019届高三理科数学三轮模拟试题】已知平面向量(vec{a})、(vec{b})满足((vec{a}-2vec{b})perp (3vec{a}+vec{b}))，且(|vec{a}|=cfrac{1}{2}|vec{b}|)，则向量(vec{a})与(vec{b})的夹角的正弦值为【】

$A.cfrac{1}{2}$ $B.-cfrac{1}{2}$ $C.cfrac{sqrt{3}}{2}$ $D.-cfrac{sqrt{3}}{2}$

分析：由题可知，((vec{a}-2vec{b})cdot (3vec{a}+vec{b})=0)，化简得到，(3vec{a}^2-5vec{a}cdot vec{b}-2vec{b}^2=0)①，

由(|vec{a}|=cfrac{1}{2}|vec{b}|)，可设(|vec{a}|=t(t>0))，则(|vec{b}|=2t)，代入①式，

得到(-10t^2cos heta+5t^2=0)，得到(cos heta=cfrac{1}{2})，则(sin heta=cfrac{sqrt{3}}{2})，故选(C).

例5【2019届高三理科数学三轮模拟训练题】公元前6世纪，黄金分割被毕达哥拉斯学派发现，公元前4世纪，古希腊数学家欧多克索斯第一个系统研究了这一问题，并建立起比例理论。欧几里得在《几何原本》中论及正五边形有关黄金分割的定理：正五边形(ABCDE)中，(AD)，(BE)交于点(H)，则(H)为(AD)的黄金分割点，即(frac{AH}{HD}=frac{sqrt{5}-1}{2})，现从如图所示的正五边形中任取一点，则该点恰好取自阴影部分的概率是【】

$A.cfrac{2}{5}$ $B.cfrac{sqrt{5}}{5}$ $C.cfrac{4}{7}$ $D.cfrac{2+sqrt{5}}{7}$

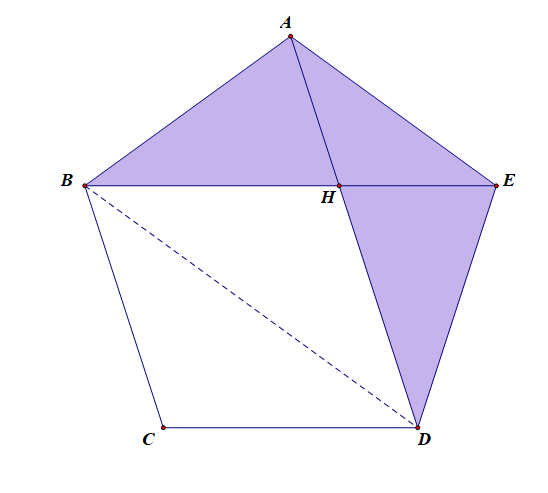
法1分析：由(frac{AH}{HD}=frac{sqrt{5}-1}{2})，借助比例因子，则可设(S_{ riangle AEH}=(sqrt{5}-1)k(k>0))，(S_{ riangle DEH}=2k)，

且有(S_{ riangle AHB}=S_{ riangle DHE})，又由于正五边形的对称性可知，(S_{ riangle ABE}=S_{ riangle BCD})，(S_{ riangle BCD}=S_{ riangle BDH})，

则(S_{ riangle ABE}=(sqrt{5}-1)k+2k=(sqrt{5}+1)k)，则(S_{阴影}=2k+2k+(sqrt{5}-1)k=(3+sqrt{5})k)，(S_{正}=2k+3cdot (sqrt{5}+1)k=(5+3sqrt{5})k)，

故所求概率为(P=cfrac{S_{阴影}}{S_{正}}=cfrac{(3+sqrt{5})k}{(5+3sqrt{5})k}=cfrac{sqrt{5}}{5})。

例6在( riangle ABC)中，已知(cfrac{a}{cosA}=cfrac{b}{cosB}=cfrac{c}{cosC})，求三角形的三个角的大小。

分析：令(cfrac{a}{cosA}=cfrac{b}{cosB}=cfrac{c}{cosC}=k)，

则有(cosA=cfrac{a}{k})，(cosB=cfrac{b}{k})，(cosC=cfrac{c}{k})，

再结合(sinA=cfrac{a}{2R})，(sinB=cfrac{b}{2R})，(sinC=cfrac{c}{2R})，

故有(tanA=tanB=tanC=cfrac{k}{2R})，故(A=B=C=cfrac{pi}{3})。

例7设等比数列({a_n})的前(n)项的和为(S_n)，若(cfrac{S_6}{S_3}=cfrac{1}{2})，则(cfrac{S_9}{S_6})=？

分析：引入比例因子，设(cfrac{S_6}{S_3}=cfrac{1}{2}=cfrac{k}{2k}(k eq 0))，则(S_6=k)，(S_3=2k)，

(S_6-S_3=-k)，由(S_3，S_6-S_3，S_9-S_6)成等比数列，可知(S_9-S_6=cfrac{k}{2})

则(S_9=cfrac{3k}{2})，故(cfrac{S_9}{S_6}=cfrac{cfrac{3k}{2}}{2k}=cfrac{3}{4})。

例8设等比数列({a_n})的前(n)项的和为(S_n)，若(cfrac{S_6}{S_3}=cfrac{1}{2})，则(cfrac{S_9}{S_6})=？

分析：引入比例因子，设(cfrac{S_6}{S_3}=cfrac{1}{2}=cfrac{k}{2k}(k eq 0))，则(S_6=k)，(S_3=2k)，

(S_6-S_3=-k)，由(S_3，S_6-S_3，S_9-S_6)成等比数列，可知(S_9-S_6=cfrac{k}{2})

则(S_9=cfrac{3k}{2})，故(cfrac{S_9}{S_6}=cfrac{cfrac{3k}{2}}{2k}=cfrac{3}{4})。

例9已知双曲线(C)的离心率为(cfrac{5}{2})，左、右焦点为(F_1)，(F_2)，点(A)在(C)上，若(|F_1A|=2|F_2A|)，则(cosangle AF_2F_1)=_______.

分析：由(e=cfrac{c}{a}=cfrac{5}{2})，令(c=5k(k>0))，则(a=2k)，(b=sqrt{21}k)，

不妨令双曲线的焦点在(x)轴，点(A)在其右支上，则由双曲线的定义可知，

(|F_1A|-|F_2A|=2a=4k)，又(|F_1A|=2|F_2A|)，

则(|F_2A|=4k)，(|F_1A|=8k)，又(|F_1F_2|=10k)，

利用余弦定理可知(cosangle AF_2F_1=cdots=cfrac{13}{20})；

---

1. 如三角形的三边之比为(a：b：c=2：3：4)，则可以设(a=2k，b=3k，c=4k(k>0))；如果求最大(小)角的余弦值，就可以直接代入余弦定理计算，同时(a，b，c)都是(k)的一元函数了。
   同样的思路也可以用到圆锥曲线中，比如已知离心率(e=cfrac{c}{a}=sqrt{3})，则可知(c=sqrt{3}t，a=t(t>0)) ，则有(b=sqrt{2}t)； ↩︎